Лабораторная работа №1 / Задания для защиты
.docxФункция Bessely
Фу́нкции Бе́сселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:
где α — произвольное вещественное число (в общем случае комплексное), называемое порядком.
Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя.
Функция Бесселя является обобщением функции синуса. Ее можно трактовать как колебание струны с переменной толщиной, переменным натяжением (или одновременно обоими условиями); колебаниями в среде с переменными свойствами; колебаниями дисковой мембраны и т. д.
Функция Бесселя второго рода:
График функции Бесселя второго рода
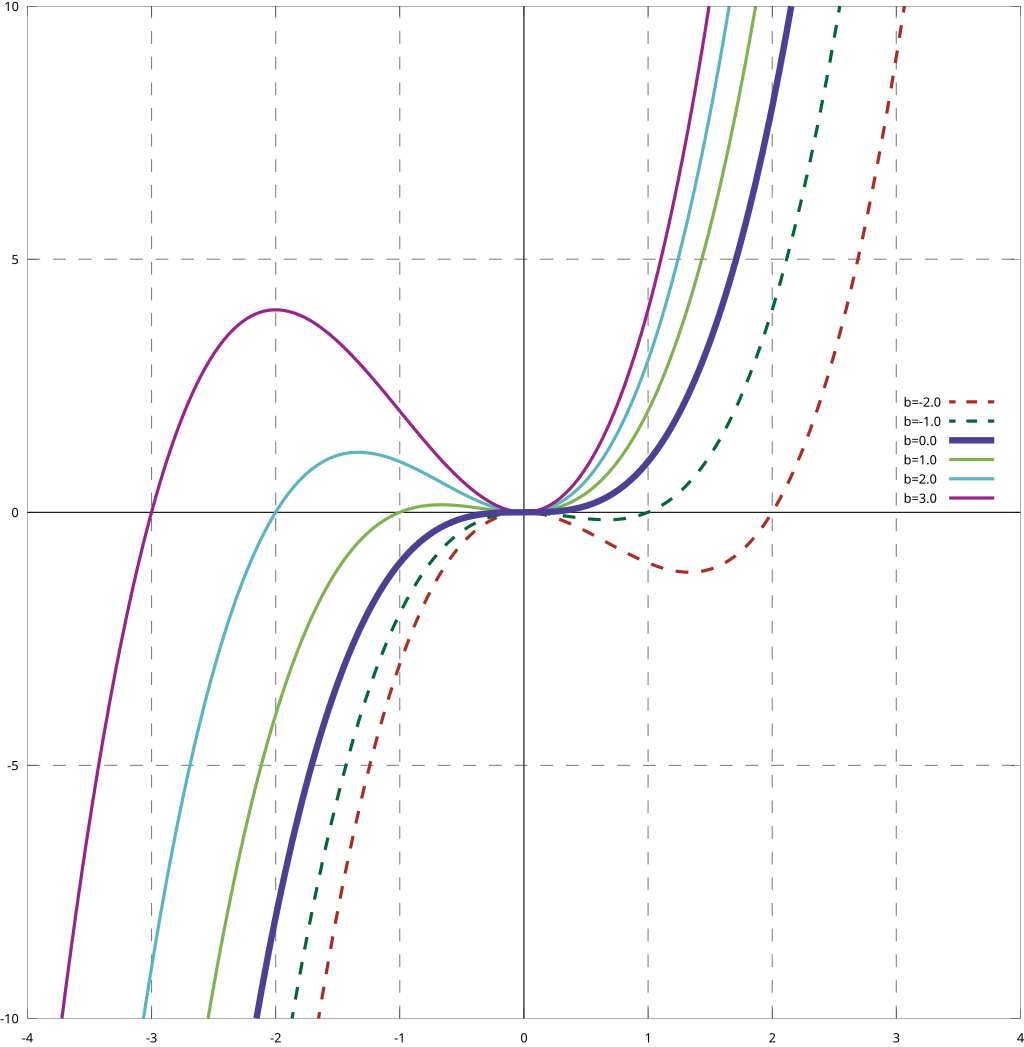
Функция Cubic
Куби́ческая фу́нкция в математике — это числовая функция
где a≠0. Другими словами, кубическая функция задаётся многочленом третьей степени.
График кубической функции называется куби́ческой пара́болой.
Функция Erf
Функция ошибок (также называемая функция ошибок Гаусса) — неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как:
Если
набор случайных величин подчиняется
нормальному распределению со стандартным
отклонением сигма, то вероятность, что
величина отклонится от среднего не
более чем на a, равна
.
Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности с начальными условиями, описываемыми функцией Хевисайда («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
