Добавил:

Julsft Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Теория вероятностей и математическая статистика

Файл:

ТВиМС 2022

.pdf

Скачиваний:

Добавлен:

01.03.2025

Размер:

1.16 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 149 10 11 12 13 14 > Следующая >>>

Как и в предыдущих пунктах полезно выбрать в качестве t1 и t2 квантили

распределения

Стьюдента

уровня

соответственно, что

обозначается как

t1 stn 1; /2 , t2

stn 1;1 /2 .

x 1

P st

n 1; /2

n 1

n 1;1 /2

n 1; /2

n 1;1 /2

n 1

P x

n 1; /2

n 1

n 1;1

1,1

2,1

Тогда 1,1; 2,1 - искомый -доверительный интервал для параметра 1 .

Использование центральной статистики не является единственным способом построения доверительных интервалов. Рассмотрим в качестве примера еще один из способов.

Пример (построение доверительного интервала для дискретной модели с помощью неравенства Чебышева).

Рассмотрим случай выборки x1,...,xn из распределения Бернулли с неизвестной вероятностью успеха 0,1 : Bi 1, .

Пусть								-
	0,1		- заданная доверительная вероятность. Построим
доверительный интервал для неизвестного параметра .
Известно, что E			E и D		D	1	.
		x		x

					n	n

Согласно классической форме неравенства Чебышева для любого 0 выполняется P x Ex Dx / 2 .

Подставим в эту формулу найденные выше значения:

Px 1 / 2n ,

1P x 1 1 / 2n ,

P x 1 1 / 2n ,

P x x 1 1 / 2n .

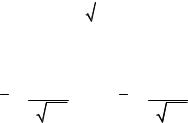
	Так		как для				любого								4
	Так		как для				любого						0,1	выражение 1	1 , то
P						1		1		.
	x				x			1
	x				x			2
								4 n
	Подберем 0 так, чтобы правая часть неравенства была равна :
	1	1		1 , 2					1		,	1		0.
	1			1 , 2					4n		,			0.
		4 2n							4n		2		n

Получили, что

P x 2 1n

x 2 1n .

Следовательно, случайный интервал 1, 2 накрывает неизвестный

параметр с вероятностью не меньшей, чем , и мы можем его рассматривать в качестве искомого -доверительного интервала.

Задания для контрольных работ.

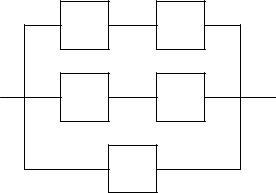
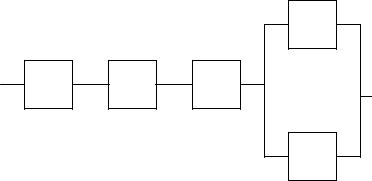
Вариант 00 1. Электрическая цепь состоит из пяти элементов, выход из строя которых в

заданный промежуток времени – независимые события, имеющие вероятности pi 0,2 каждый. Найти вероятность P отказа цепи за данный промежуток времени.

2. Дискретная случайная величина задана законом распределения

pi (xi ).

Найти величину a, построить график функции распределения данной случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины.

xi	0	2	4	6	8
pi	0,1	0,2	0,3	0,2	a

3. Плотность распределения вероятностей непрерывной случайной величины задана выражением:

0;	x 0
	0 x 6
f (x) ax2 ;	0 x 6
	x 6
0;	x 6

Найти величину коэффициента a, написать аналитическое выражение и простроить график функции распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы (0, 4) и (4, 10).

4.Дана нормально распределенная случайная величина с математическим ожиданием m 5 и дисперсией 2 3. Найти вероятность того, что абсолютная величина отклонения случайной величины от ее математического ожидания меньше 4.

5.Дискретная случайная величина задана выборкой:

0, -1, 0, 1, 1, -1, -1, 0, 0, 0, -1, 0, 1, 1, 0, -1, 0, 0, 0, 1, 1, 1, -1, 1, 1

Построить полигон частот и эмпирическую функцию распределения. Найти выборочное среднее и выборочную дисперсию.

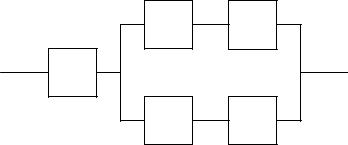
Вариант 01 1. Электрическая цепь состоит из пяти элементов, безотказная работа

которых в заданный промежуток времени – независимые события, имеющие вероятности qi 0,9 каждый. Найти вероятность Q безотказной работы цепи за данный промежуток времени.

2. Дискретная случайная величина задана законом распределения

pi (xi ).

xi	0	1	2	3	4
pi	0,2	0,2	0,3	0,1	a

3. Плотность распределения вероятностей непрерывной случайной величины задана выражением:

0;	x 3
	3 x 1
f (x) a;	3 x 1
	x 1
0;	x 1

случайной величины. Найти вероятности попадания данной случайной величины в интервалы ( 2,0) и (0, 4).

4.Вероятность попадания нормально распределенной случайной величины с математическим ожиданием m 4 в интервал (3; 5) равна 0,6. Найти дисперсии данной случайной величины.

5.Дискретная случайная величина задана выборкой:

0, -1, 0, 1, 1, -1, -1, 0, 0, 0, -1, 0, 1, 1, 0, -1, 0, 0, 0, 1, 1, 1, -1, 1, 1

Вариант 02 1. Последовательность передаваемых сигналов состоит из независимо

передаваемых точек и тире, причем количество точек в этом потоке в среднем в пять раз больше, чем тире. Вероятность правильного приема точки p1 0,7, тире p2 0,8. Найти вероятность того, что произвольно взятый сигнал будет принят с ошибкой.

2. Дискретная случайная величина задана законом распределения pi (xi ). Найти величину a, построить график функции распределения данной случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины.

xi	0	2	4	6	8
pi	a	0,2	0,4	0,2	0,1

3. Плотность распределения вероятностей непрерывной случайной величины задана выражением:

0;	x 0
	0 x 6
f (x) a;	0 x 6
	x 6
0;	x 6

5.Непрерывная случайная величина задана упорядоченной выборкой.

(xi 1;xi )	[4; 6)	[6; 8)	[8; 10)	[10; 12)	[12; 14]

ni	30	30	70	40	30

Построить гистограмму и эмпирическую функцию распределения. Найти выборочное среднее и выборочную дисперсию.

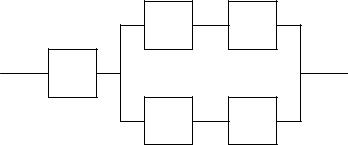
Вариант 03 1. Электрическая цепь состоит из пяти элементов, выход из строя которых в

заданный промежуток времени – независимые события, имеющие вероятности pi 0,1 каждый. Найти вероятность P отказа цепи за данный промежуток времени.

2. Дискретная случайная величина задана законом распределения

pi (xi ).

xi	0	2	4	6	8
pi	0,2	a	0,3	0,2	0,1

3. Плотность распределения вероятностей непрерывной случайной величины задана выражением:

0;	x 0
	0 x 6
f (x) ax3 ;	0 x 6
	x 6
0;	x 6

4.Дана нормально распределенная случайная величина с математическим ожиданием m 6 и дисперсией 2 4. Найти вероятность попадания данной случайной величины в интервал (3;8).

5.Непрерывная случайная величина задана упорядоченной выборкой.

(xi 1;xi )	[4; 6)	[6; 8)	[8; 10)	[10; 12)	[12; 14]

ni	30	30	70	40	30

Вариант 04 1. Сообщение состоит из пяти сигналов, причем вероятности безошибочного

приема каждого сигнала одинаковы и равны p 0,6. Сообщение будет принято, если из пяти сигналов принято хотя бы три. Найти вероятность того, что передаваемое сообщение не принято.

xi	0	1	2	3	4
pi	0,2	0,2	a	0,2	0,1

3. Плотность распределения вероятностей непрерывной случайной величины задана выражением:

0;	x 3
	3 x 3
f (x) a;	3 x 3
	x 3
0;	x 3

4.Дана нормально распределенная случайная величина с математическим ожиданием m 4 и дисперсией 2 3. Найти вероятность того, что абсолютная величина отклонения случайной величины от ее математического ожидания меньше 1.

5.Найти выборочный коэффициент корреляции для пары случайных величин:

Y	-1	0	1
X
0	10	0	20
2	20	10	40

Вариант 05 1. Сообщение состоит из пяти сигналов, причем вероятности безошибочного

приема каждого сигнала одинаковы и равны p 0,7. Сообщение будет принято, если из пяти сигналов принято по крайней мере три. Найти вероятность того, что передаваемое сообщение не принято.

xi	-2	-1	0	1	2
pi	0,1	0,2	0,2	0,2	a

3. Функция распределения непрерывной случайной величины задана выражением:

0;	x 0
	0 x 4
F(x) ax3 ;	0 x 4
	x 4
1;	x 4

Найти величину коэффициента a, написать аналитическое выражение и простроить графи плотности распределения вероятностей, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы (0, 2) и (2, 10).

5.Непрерывная случайная величина задана упорядоченной выборкой.

(xi 1;xi )	[4; 6)	[6; 8)	[8; 10)	[10; 12)	[12; 14]
ni	5	20	50	20	5

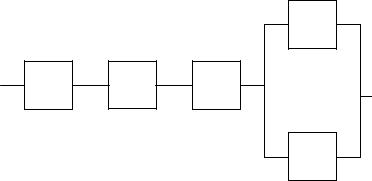
Вариант 06 1. Электрическая цепь состоит из пяти элементов, безотказная работа

2. Дискретная случайная величина задана законом распределения

pi (xi ).

xi	0	2	4	6	8
pi	a	0,2	0,4	0,2	0,1

3. Плотность распределения вероятностей непрерывной случайной величины задана выражением:

0;	x 2
	2 x 2
f (x) a;	2 x 2
	x 2
0;	x 2

4.Вероятность попадания нормально распределенной случайной величины с математическим ожиданием m 5 в интервал (4; 6) равна 0,8. Найти дисперсии данной случайной величины.

5.Дискретная случайная величина задана выборкой:

1, 2, 3, 3, 3, 3, 3, 1, 1, 1, 2, 3, 3, 1, 1, 1, 1, 3, 3, 1, 1, 1, 2, 3, 1

Вариант 07 1. Электрическая цепь состоит из пяти элементов, выход из строя которых в

2. Дискретная случайная величина задана законом распределения

pi (xi ).

xi		1	3	5	7	9
pi		0,1	0,2	0,3	a	0,1
	3. Функция распределения непрерывной случайной величины задана
выражением:			0;	x 0
			0;	x 0
				0 x 2
			F(x) ax;	0 x 2
				x 2
			1;	x 2

4.Дана нормально распределенная случайная величина с математическим ожиданием m 2 и дисперсией 2 3. Найти вероятность попадания данной случайной величины в интервал (0; 4).

5.Дискретная случайная величина задана выборкой:

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 149 10 11 12 13 14 > Следующая >>>