Падение плоской волны на диэлектрическую пластину

Рассмотрим волновые явления при падении плоской волны на диэлектрическую пластину, помещенную в диэлектрическую среду с относительной проницаемостью _r1 (Рисунок 4). Область над пластиной назовем средой 1, под пластиной – средой 3. Обозначим относительную проницаемость пластины (среда 2) через _r2, толщину пластины через t.

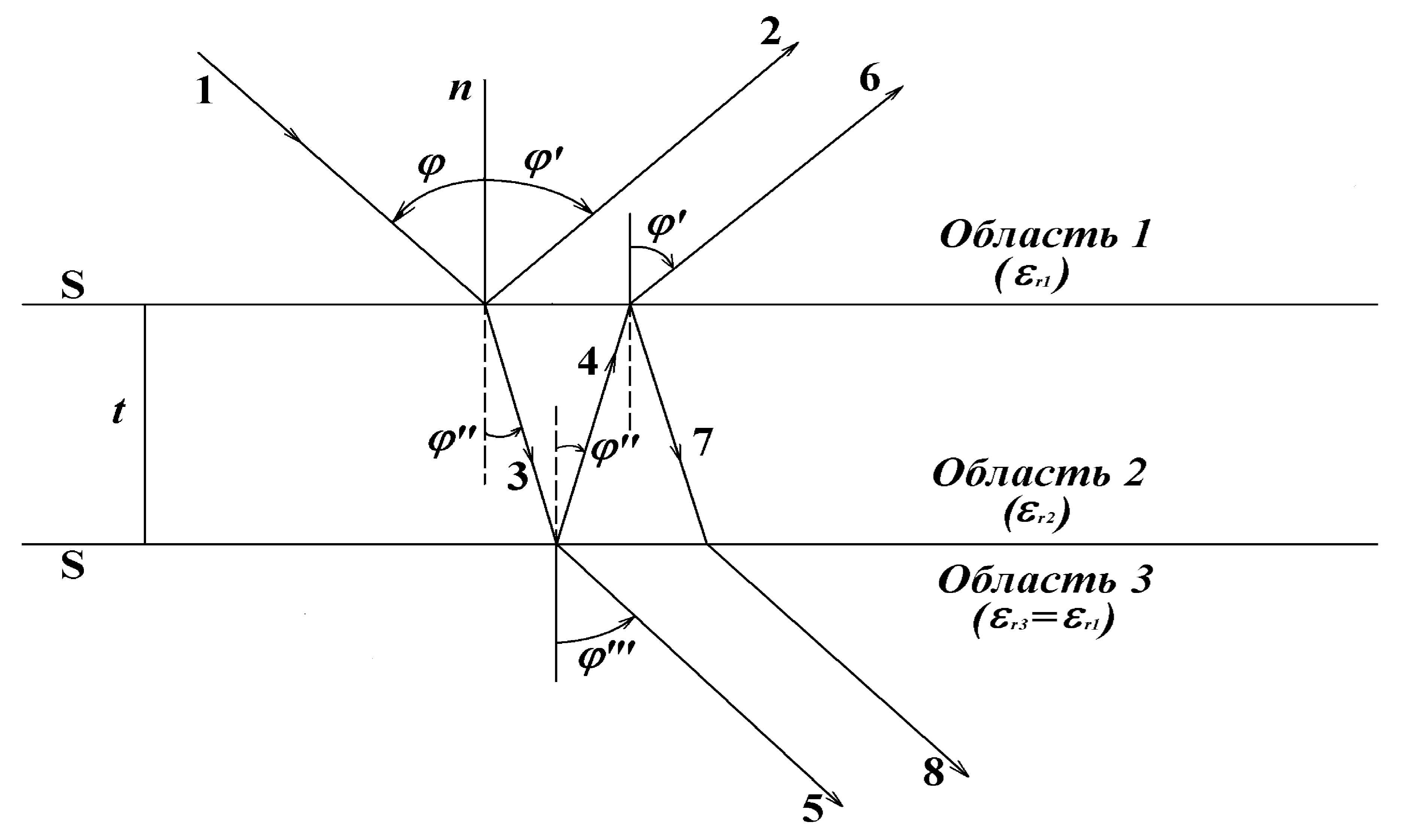
Рисунок 4 – Падение плоской волны на диэлектрическую пластину

Оказывается, что волновые явления в этом случае получаются гораздо более сложными, чем при наличии только одной границы раздела двух сред. Действительно, волна, падающая на пластину из области 1 под углом  (обозначим ее цифрой 1 на Рисунке 4), частично отразится от верхней границы под углом  =  (волна 2), а частично пройдет внутрь пластины под углом  (волна 3). Прошедшая внутрь пластины волна 3 в свою очередь частично отразится от нижней границы (волна 4), а частично пройдет под углом  в область 3 (волна 5). Волна 4, отразившаяся от нижней границы, преломится на верхней границе (волна 6), причем направление распространения этой волны в области 1 совпадает с углом , под которым распространяется волна 2 после первичного отражения от верхней границы. Другая часть волны 4 отразится от верхней границы (волна 7) и, преломившись на нижней границе, будет распространяться в области 3 (волна 8) под тем же углом , что и волна 5 после первичного прохождения через нижнюю границу. Можно показать с помощью законов Снеллиуса (1), что  = .

Подобные процессы отражения и преломления волн повторяются бесчисленное число раз. Однако суммарное отраженное поле в области 1 будет представлять собой, как и при отражении от границы раздела двух сред, однородную плоскую волну, бегущую под углом  = , отличие будет состоять лишь в амплитуде этой волны, которую характеризует коэффициент отражения R_.

Суммарное поле, прошедшее через пластину, т.е. поле в области 3, будет также представлять собой плоскую волну, распространяющуюся под углом  = . Амплитуда этой волны характеризуется коэффициентом Т_. Суммарное поле внутри пластины (область 2) представляет собой сумму двух плоских волн с разными в общем случае амплитудами, бегущих под углом  – 2 друг к другу.

Коэффициент отражения для рассматриваемого случая может быть определен по формуле

. (7)

Переходя к модулям, получаем

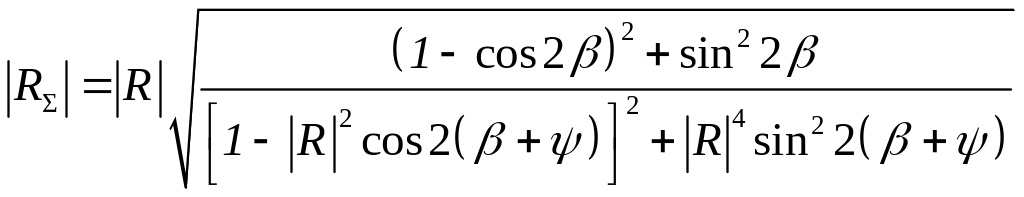, (8)

где 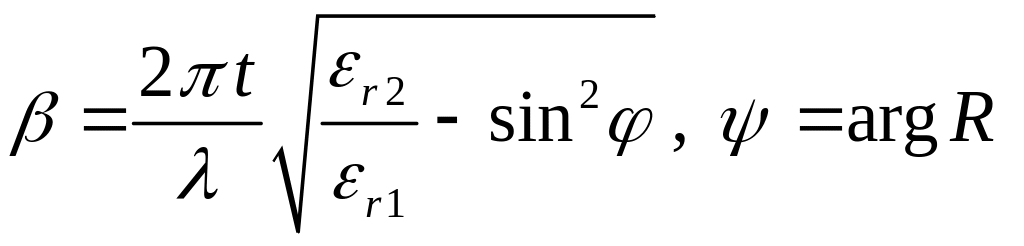, R – вычисляется по формулам (2) или (4),  – длина волны в вакууме .

Поскольку все три волны (падающая, отраженная в области 1 и преломленная в области 3) распространяются под одним и тем же углом по отношению к нормали и в одной и той же среде, между модулями коэффициентов отражения и преломления существует связь вида

. (9)

Эта связь вытекает из равенства мощности преломленной волны разности мощностей, переносимых падающей и отраженной волнами.

Анализ выражения (7) показывает, что для параллельной поляризации при падении волны под углом Брюстера ( = _бр) коэффициент отражения обращается в ноль при любой толщине пластины t. Это можно объяснить тем, что в соответствии с законами Снеллиуса при  = _бр величина угла ", определяемая соотношением , в точности соответствует значению угла Брюстера при падении волны 3 из среды 2 на границу раздела со средой 3, имеющей относительную проницаемость _r1 (см. Рисунок 4). Другими словами, при падении волны на пластину под углом  = _бр отражение не возникает не только от верхней, но и от нижней границы при произвольной толщине пластины.

При произвольном угле падения и произвольной поляризации падающей волны можно добиться равенства нулю коэффициента отражения, подбирая толщину пластины (при заданном значении _r2) или проницаемость _r2 (при заданной толщине). Действительно, как следует из (7), величина R_.= 0 при , где m = 1, 2, 3, … . Отсюда получаем (при заданном значении _r2) толщину пластины, при которой R_.= 0:

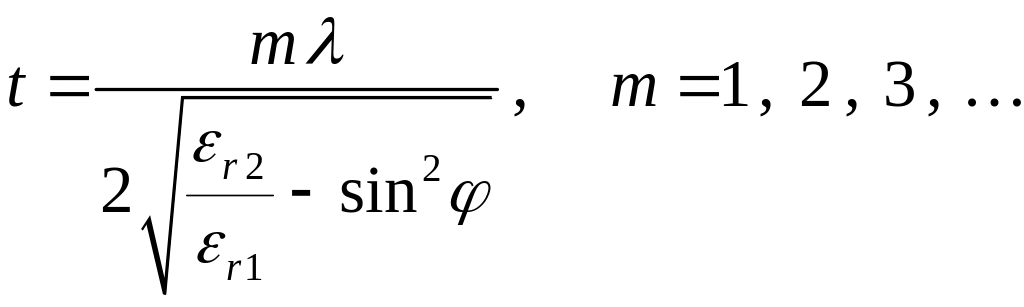(10)

При нормальном падении волны и _r1 = 1 величина R_.= 0, если:

, (11)

где – длина волны в среде 2, т.е. внутри пластины.

Для случая разнородных сред вокруг пластины ( ) равенство R_.= 0 при нормальном падении волны имеет место при выполнении условий:

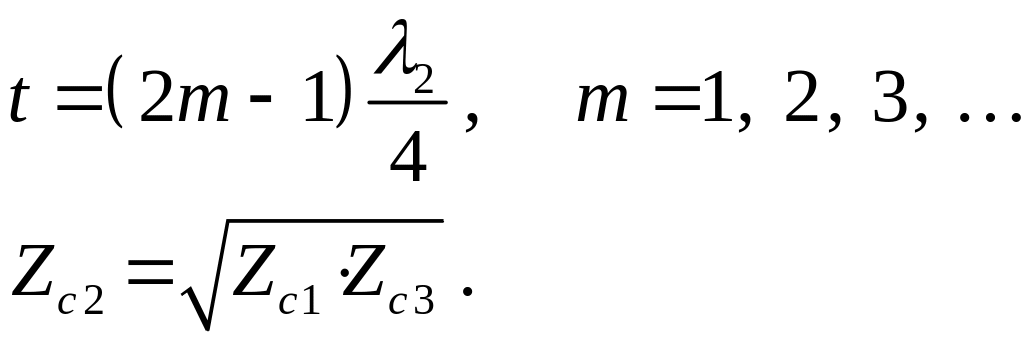(12)

Минимальная толщина такой пластины должна быть равна четверти длины волны в пластине, а ее характеристическое сопротивление равняться среднему геометрическому значению от характеристических сопротивлений окружающих пластину сред.

В заключение отметим, что при облучении плоской волной пластины, окруженной менее плотной средой (_r2 > _r1), явления полного внутреннего отражения возникнуть не может.

Однако при определенных условиях возбуждения диэлектрическая пластина, окруженная менее плотной средой, например, воздухом, способна поддерживать поверхностную волну, которая распространяется вдоль нее. В этом случае пластина выступает как диэлектрический волновод – структура, направляющая волновой процесс.

14