
5. Задание к экспериментальной части
5.1. На частоте, заданной преподавателем, снять кривую распределения амплитуды поля в продольном сечении волновода, замкнутом накоротко, и по найденному распределению определить длину волны в волноводе.
5.2.
Измерить коэффициент бегущей волны
(КБВ) и смещение узла напряженности
электрического поля
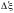 при
заданной преподавателем нагрузки линии
относительно узла при коротком замыкании.
при
заданной преподавателем нагрузки линии
относительно узла при коротком замыкании.
5.3 По круговой диаграмме полных сопротивлений определить нормированное сопротивление и нормированную проводимость включенной нагрузки, а также место включения и нормированную проводимость согласующего элемента (расчет произвести для емкостного согласующего элемента).
5.4 Настроить волновод в режим бегущей волны с помощью емкостного штыря.
6. Порядок и методика выполнения работы
6.1 Включить генератор. Замкнуть волновод накоротко и передвигая зонд по всей длине измерительной линии, снять кривую распределения напряженности электрического поля в продольном сечении волновода. Методом вилки уточнить положение нулей (узлов амплитуды напряженности электрического поля). Достаточно определить координаты любых двух соседних узлов М1 и М2
6.2
По данным, полученным при выполнении
п.6.1, определить длину волны в волноводе
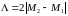
6.3. Установить зонд измерительной линии в один из узлов. Ввести емкостной штырь согласующей секции и передвигая его вдоль секции, определить в ней положение узла ( в узле изменение глубины погружения не изменяет показания микроамперметра). Записать положение узла в согласующей секции. Вывести штырь
6.4
На выходе волновода заменить
короткозамыкающую пластину заданной
нагрузкой. Измерить КБВ и
в
линии. Величина КБВ находится путем
измерения наибольшего(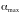 )
и наименьшего(
)
и наименьшего(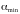 )
показания микроамперметра при передвижении
подвижного зонда вдоль измерительной
линии. Так как характеристика
кристаллического детектора при малых
сигналах почти квадратична, то показания
прибора пропорциональны квадрату
напряжения, приложенного к детектору.
Поэтому
)
показания микроамперметра при передвижении
подвижного зонда вдоль измерительной
линии. Так как характеристика
кристаллического детектора при малых
сигналах почти квадратична, то показания
прибора пропорциональны квадрату
напряжения, приложенного к детектору.
Поэтому
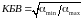 .
Для определения
нужно найти положение узла амплитуды
напряженности при исследуемой нагрузки
.
Для определения
нужно найти положение узла амплитуды
напряженности при исследуемой нагрузки
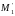 и определить расстояние от него до
ближайшего узла при коротком замыкании
М1.
Тогда
и определить расстояние от него до
ближайшего узла при коротком замыкании
М1.
Тогда
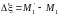
6.5
По найденным в п.6.4 значениям КБВ и
отношению
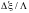 с учетом направления смещения узла
необходимо определить нормированное
сопротивление и нормированную проводимость
нагрузки.
с учетом направления смещения узла
необходимо определить нормированное
сопротивление и нормированную проводимость
нагрузки.
6.6. По найденной в п.6.5 нормированной проводимости нагрузки с помощью круговой диаграммы необходимо определить сечение линии, в которое следует вводить емкостной штырь для настройки линии в режим бегущей волны.
6.7
Передвинуть емкостной штырь согласующей
секции на рассчитанное в п.6.6 расстояние
от точки, соответствующей узлу в режиме
КЗ, определенной в п.6.3. Постепенно
изменяя глубину погружения штыря,
настроить волноводную линию в режим
бегущей волны. При изменении глубины
погружения штыря зонд измерительной
линии должен находиться либо в узле
амплитуды напряженности электрического
поля, либо в пучности. Линия считается
настроенной в режим бегущей волны если
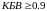 .
.
6.8 Оформить отчет и представить его преподавателю
СОДЕРЖАНИЕ ОТЧЕТА
Цель работы.
Блок-схема лабораторной установки.
Результаты домашнего расчета (см. раздел 3).
Значения величин, полученных экспериментально.
График, характеризующий распределение амплитуды поля в продольном сечении волновода при КЗ по данным, полученным в п.6.1
Результаты расчета положения согласующего элемента
Результаты согласования (величина КБВ после настройки)
Краткие выводы по работе
КОНТРОЛЬНЫЕ ВОПРОСЫ
Что такое коэффициент отражения, коэффициент бегущей волны и коэффициент стоячей волны и от чего они зависят?
Включению какой нагрузки эквивалентно присоединение короткозамкнутого отрезка линии длиной
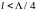 и
и
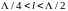 ?
?Куда сдвигается минимум амплитуды напряжения в линии по сравнению с ближайшим узлом при КЗ при чисто емкостной нагрузке на конце линии? Объяснить результат
То же самое, что в п.8.3, но при чисто индуктивной нагрузке.
То же самое, что в п.8.3, но при чисто активной нагрузке. Рассмотреть три случая
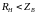 ,
,
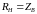 и
и
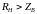 .
Для указанных случаев показать
зависимость амплитуды напряжения
.
Для указанных случаев показать
зависимость амплитуды напряжения
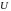 от
координаты
от
координаты
 ,
изменяющейся вдоль линии.
,
изменяющейся вдоль линии.То же самое, что и в пп.8.3…8.5, но при учете потерь в линии передачи.
От чего зависит длина волны в волноводе?
На основе каких соображений проводится анализ распространения электромагнитных волн в волноводах конечной длины?
Что называют входным, нормированным входным, эквивалентным, нормированным эквивалентным и волновым сопротивлением линии передачи?
На основе каких соображений вводится понятие длинной линии, эквивалентной волноводу? Как определяется волновое сопротивление волновода?
В чем состоит метод измерения сопротивления линии?
С какой целью стремятся согласовать сопротивление нагрузки с волновым сопротивлением линии? нове каких методов может быть решена задача согласования?
В чем состоит метод согласования линии с помощью реактивного элемента?
В чем состоит метод согласования с помощью четвертьволновой вставки?
Как осуществляется широкополосное согласование?
Для чего в волноводных линиях передачи используют диафрагмы? Перечислите типы диафрагм, объясните их принцип действия. Нарисуйте эквивалентные схемы диафрагм.
СПИСОК ЛИТЕРАТУРЫ
1. Седов. В.М, Гайнутдинов Т.А. Электромагнитные поля и волны. - М. Горячая линия Телеком, 2017. с. 210-238
2. Пименов Ю.В., Вольман В.И., Муравцов А.Д. Техническая электродинамика.- М:Радио и Связь, 2000. с.360-388, с.401-407
3. Сазонов Д.М. Антенны и устройства СВЧ.- М. Высшая школа. 1988. с. 36-47
ПРИЛОЖЕНИЯ
П.1 ЭКВИВАЛЕНТНОЕ СОПРОТИВЛЕНИЕ ЛИНИИ И ФОРМУЛА ТРАНСФОРМАЦИИ
При анализе процессов, происходящих в линиях передачи конечной длины, обычно пользуются методами теории длинных линий, основанных на концепции падающих и отраженных волн. Структура каждой, отдельной падающей или отраженной волны предполагается такой же, как в линии бесконечной длины. Напряжение и ток в длинной линии рассматриваются соответственно как суммы напряжений и токов падающей и отраженной волны
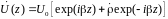 ,
,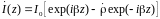 ,
(1)
,
(1)
где
 -
расстояние от конца линии (нагрузки) до
исследуемого сечения линии,
-
расстояние от конца линии (нагрузки) до
исследуемого сечения линии,
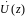 и
и
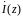 -комплексные амплитуды напряжения и
тока в исследуемом сечении,
-комплексные амплитуды напряжения и
тока в исследуемом сечении,
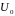 и
и
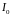 - амплитуды напряжения и тока в падающей
волне,
- амплитуды напряжения и тока в падающей
волне,
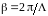 -
коэффициент фазы,
-
коэффициент фазы,
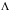 -
длина волны в линии,
-
длина волны в линии,
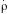 -
коэффициент отражения по напряжению.
-
коэффициент отражения по напряжению.
Отношение
амплитуд напряжения и тока в бегущей
(падающей) волне равно волновому
сопротивлению линии
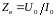 .
Отношение комплексных амплитуд напряжения
и тока в сечении линии
называют эквивалентным сопротивление
линии
.
Отношение комплексных амплитуд напряжения
и тока в сечении линии
называют эквивалентным сопротивление
линии
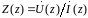 .
Эквивалентное сопротивление линии
.
Эквивалентное сопротивление линии
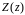 имеет
ясный физический смысл. Если обрезать
линию в сечении z (от
генератора до сечения с координатой z)
и нагрузить оставшуюся часть линии на
сопротивление нагрузки численно равное
,
то распределение амплитуд напряжения
и тока в оставшейся части линии останется
таким же как и до обрезания. Эквивалентное
сопротивление, вычисленное для сечения,
соответствующего входу линии (
имеет
ясный физический смысл. Если обрезать
линию в сечении z (от
генератора до сечения с координатой z)
и нагрузить оставшуюся часть линии на
сопротивление нагрузки численно равное
,
то распределение амплитуд напряжения
и тока в оставшейся части линии останется
таким же как и до обрезания. Эквивалентное
сопротивление, вычисленное для сечения,
соответствующего входу линии (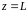 )
называют входным сопротивлением линии
)
называют входным сопротивлением линии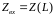 ,
где
,
где
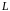 -
длина линии. В конце линии (в сечении
нагрузки
-
длина линии. В конце линии (в сечении
нагрузки
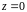 )
эквивалентное сопротивление равно
сопротивлению нагрузки
)
эквивалентное сопротивление равно
сопротивлению нагрузки
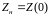 .
Очевидно, что эквивалентное сопротивление
линии в сечении
равно входному сопротивлению отрезка
линии длиной
,
нагруженного на сопротивление
.
Очевидно, что эквивалентное сопротивление
линии в сечении
равно входному сопротивлению отрезка
линии длиной
,
нагруженного на сопротивление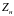 .
.
Отношение
эквивалентного сопротивления к волновому
сопротивлению называют нормированным
эквивалентным сопротивлением линии
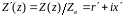 .
Соответственно величины
.
Соответственно величины
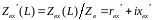 и
и
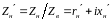 называют нормированным входным
сопротивлением линии и нормированным
сопротивление нагрузки. Помимо
нормированных сопротивлений используют
и нормированные проводимости. Нормированная
эквивалентная проводимость линии
определяется как
называют нормированным входным
сопротивлением линии и нормированным
сопротивление нагрузки. Помимо
нормированных сопротивлений используют
и нормированные проводимости. Нормированная
эквивалентная проводимость линии
определяется как
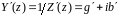 .
Нормированная входная проводимость
линии и нормированная проводимость
нагрузки определяются аналогично
.
Нормированная входная проводимость
линии и нормированная проводимость
нагрузки определяются аналогично
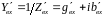 ,
,
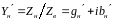
Волновод является одним из видов линии передачи, поэтому полученные в теории длинных линий результаты можно использовать и при рассмотрении волноводов. Во многих случаях, особенно связанных с оценкой эффективности переноса мощности электромагнитного поля по волноводу, оказывается удобным вместо волновода рассматривать эквивалентную ему двухпроводную длинную линию [1,2].
В
волноводной технике стараются пользоваться
только нормированными сопротивлениями
и проводимостями [1-3]. Из теории длинных
линий [1-3] известна формулы, связывающая
между собой нормированное эквивалентное
сопротивление (проводимость) в сечении
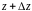 с нормированным эквивалентным
сопротивлением (проводимостью) в сечении
с нормированным эквивалентным
сопротивлением (проводимостью) в сечении
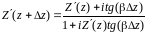 ,
,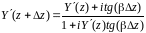 .
(2)
.
(2)
Формулы
(2) показывают как трансформируется
эквивалентное сопротивление (проводимость)
вдоль длинной линии, поэтому эти формулы
принято называть формулами трансформации.
Частным случаем формул трансформации
(формул пересчета) является ситуация,
когда в качестве начального сечения
выбирается сечение нагрузки
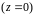 ,
и формулы (2) приобретают вид
,
и формулы (2) приобретают вид
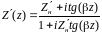 ,
,
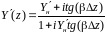 .
(3)
.
(3)
Из
(2) видно, что
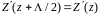 ,
,
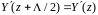 .
Отсюда
следует, что эквивалентные нормированные
сопротивления (проводимости) являются
периодическими функциями продольной
координаты
с периодом
.
Отсюда
следует, что эквивалентные нормированные
сопротивления (проводимости) являются
периодическими функциями продольной
координаты
с периодом
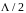 ,
поэтому для полного описания трансформации
эквивалентных сопротивлений (проводимостей)
вдоль длинной линии достаточно определить
эти величины на любом удобном интервале
длиной
.
Эквивалентные сопротивления (проводимости)
связаны с величиной коэффициента
отражения
и
КБВ следующими соотношениями
,
поэтому для полного описания трансформации
эквивалентных сопротивлений (проводимостей)
вдоль длинной линии достаточно определить
эти величины на любом удобном интервале
длиной
.
Эквивалентные сопротивления (проводимости)
связаны с величиной коэффициента
отражения
и
КБВ следующими соотношениями
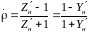 ,
,
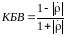 .
(4)
.
(4)
П.2 КРУГОВАЯ ДИАГРАММА ПОЛНЫХ СОПРОТИВЛЕНИЙ И ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ НАГРУЗКИ
Сравнительно высокая трудоемкость вычислений по формулам (2) и (4), необходимых для определения энергетической эффективности процесса переноса мощности по линии передачи привела к созданию специального устройства, необходимого для упрощения расчетов по (2), (4) при сохранении приемлемой с инженерной точки зрения точности. Данное устройство получило название круговая диаграмма полных сопротивлений (диаграмма Вольперта-Смитта). В дальнейшем мы не будем использовать термин нормированные сопротивления и проводимости, а просто говорить о сопротивлениях и проводимостях, поскольку круговая диаграмма используют только нормированные величины Общий вид диаграммы приведен на рис.2, а вид в масштабе, достаточном для проведения практических расчетов, в приложении 4
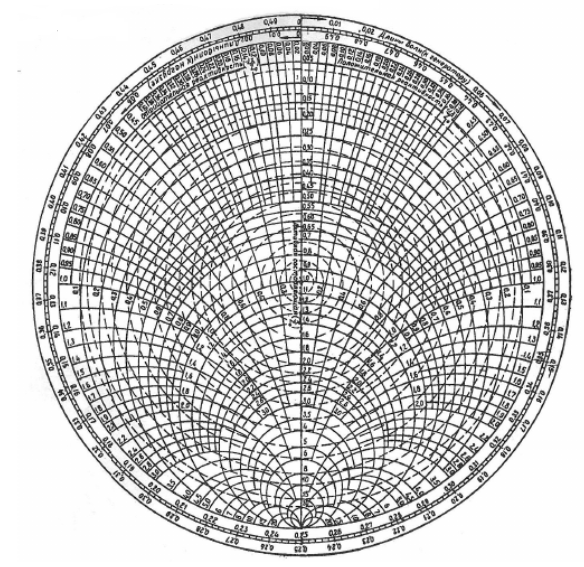
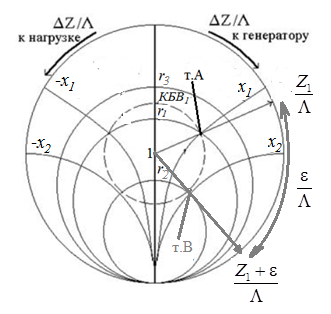
Рис.2 Рис.3
На круговой диаграмме полных сопротивлений нанесено три семейства кривых, внешняя окружность с указанием направления пересчета и один вертикальный отрезок (см. рис.2, приложение 4, а также [2,3]). Для большей наглядности на рис.3 приведены некоторые из этих семейств:
Вертикальный отрезок чисто активных сопротивлений (проводимостей) (x=0). На этом отрезке в логарифмическом масштабе откладываются числа, причем центром отрезка (центром круговой диаграммы) является число 1, верхнем концом отрезка 0, а нижнем
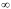 .
В нашем примере, изображенном на рис.3
на этом отрезке отложены четыре числа
r1,
r2,
КБВ1,r3
.
В нашем примере, изображенном на рис.3
на этом отрезке отложены четыре числа
r1,
r2,
КБВ1,r3
Семейство сплошных окружностей r=const с центрами на вертикальной оси. Эти окружности получили названия окружности равных активных сопротивлений (проводимостей). Любая точка лежащая на этой окружности имеет постоянное активное сопротивление (проводимость). На рис.3 указаны три таких окружности с постоянным сопротивлением r1, r2, r3.
Семейство пунктирных окружностей
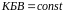 с
центром в середине вертикального
отрезка чисто активных сопротивлений.
Эти окружности получили название
окружностей равного КБВ. Любая точка
лежащая на этой окружности имеет
постоянный КБВ. На рис. 3. указана одна
из этих окружностей с КБВ=КБВ1.
Для определения величины этого КБВ
достаточно найти координату пересечения
этой окружности с верхней частью
вертикального отрезка. Координата
пересечения окружности постоянного
КБВ с нижней частью вертикального
отрезка определяет величину коэффициента
стоячей волны (КСВ), который равен 1/КБВ.
с
центром в середине вертикального
отрезка чисто активных сопротивлений.
Эти окружности получили название
окружностей равного КБВ. Любая точка
лежащая на этой окружности имеет
постоянный КБВ. На рис. 3. указана одна
из этих окружностей с КБВ=КБВ1.
Для определения величины этого КБВ
достаточно найти координату пересечения
этой окружности с верхней частью
вертикального отрезка. Координата
пересечения окружности постоянного
КБВ с нижней частью вертикального
отрезка определяет величину коэффициента
стоячей волны (КСВ), который равен 1/КБВ.
Семейство дуг окружностей x=const , имеющих общую точку в нижнем конце вертикального отрезка. Эти дуги получили название дуги равных реактивных сопротивлений (проводимостей). Любая точка, лежащая на этой дуге имеет постоянное реактивное сопротивление (проводимость). Дуги, соответствующие положительным значениям x находятся справа от отрезка чисто активных сопротивлений, а дуги, соответствующие отрицательным значениям x слева. На рис.3 представлены две дуги с положительным реактивным сопротивлением х1, x2 , и две дуги с отрицательными реактивными сопротивлениями -х1,-x2 . Для определения конкретной величины реактивного сопротивления дуги необходимо определить координату пересечения дуги с внешним кругом круговой диаграммы.
Внешняя окружность по которой откладывается расстояние пересчета
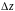 сопротивлений
(проводимостей) и направление пересчета
( к генератору по часовой стрелке, к
нагрузке против часовой стрелки, как
показано на рис.3). Так как круговая
диаграмма используется для пересчета
сопротивлений (проводимостей) для
различных линий, работающих в разных
частотных диапазонах, величины начальной
координаты
и расстояние пересчета
на
круговой диаграмме указывается в долях
длины волны в линии
сопротивлений
(проводимостей) и направление пересчета
( к генератору по часовой стрелке, к
нагрузке против часовой стрелки, как
показано на рис.3). Так как круговая
диаграмма используется для пересчета
сопротивлений (проводимостей) для
различных линий, работающих в разных
частотных диапазонах, величины начальной
координаты
и расстояние пересчета
на
круговой диаграмме указывается в долях
длины волны в линии
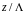 и
и
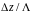 .
Верхняя
точка внешней окружности располагается
в верхнем конце вертикального отрезка
и соответствует нормированной координате
=0,
нижняя точка внешней окружности
совпадает с нижним концом вертикального
отрезка и соответствует координате
.
Верхняя
точка внешней окружности располагается
в верхнем конце вертикального отрезка
и соответствует нормированной координате
=0,
нижняя точка внешней окружности
совпадает с нижним концом вертикального
отрезка и соответствует координате
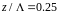 .
После перехода через нижнюю точку
окружности пересчета идет дальнейший
рост нормированной координаты и по
достижению полного круга координата
проходит путь 0.5
,
что вытекает из свойств периодичности
эквивалентного сопротивления
(проводимости)
.
После перехода через нижнюю точку
окружности пересчета идет дальнейший
рост нормированной координаты и по
достижению полного круга координата
проходит путь 0.5
,
что вытекает из свойств периодичности
эквивалентного сопротивления
(проводимости)
Таким образом, каждой точке на круговой диаграмме соответствует единственное. Вполне определенное значение комплексного сопротивления, определяемого точкой пересечения линий b) и d). Например, если на круговой диаграмме нужно отобразить комплексное нормированное сопротивление z1=r1+ix1 необходимо найти пересечение окружности r=r1 и дуги x=x1 . Пересечение этой окружности и дуги есть точка А, показанная на рис.3 и именно эта точка символизирует сопротивление z1=r1+ix1. Отметим, что принципы отображения комплексных величин на круговой диаграмме одинаковы для сопротивлений и проводимостей, поэтому точка А отображает и комплексную нормированную проводимость y1 , численно совпадающую с комплексным нормированным сопротивлением z1.
Пересчет
эквивалентных сопротивлений (проводимостей)
по круговой диаграмме выполняется
предельно просто. Допустим необходимо
пересчитать эквивалентное нормированное
сопротивление z1
(точка А) на расстояние
 в
сторону к генератору. Для этого выполняются
следующие операции
в
сторону к генератору. Для этого выполняются
следующие операции
Из центра круговой диаграммы (точка 1) проводится отрезок, проходящий через точку А и оканчивающийся на внешний окружности. На конце отрезка, в точке на внешней окружности определяется нормированная координата
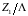 (см.рис.3).
(см.рис.3).
В направлении пересчета, в нашем случае по часовой стрелке, т.к. пересчет идет по направлению к генератору, по внешней окружности откладывается величина
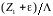 ,
как
показано на рис.3. Если бы требовался
пересчет в сторону нагрузки, процедура
была бы аналогична, но величина
откладывалась
против часовой стрелки.
,
как
показано на рис.3. Если бы требовался
пересчет в сторону нагрузки, процедура
была бы аналогична, но величина
откладывалась
против часовой стрелки.
Из центра круговой диаграммы проводится отрезок, оканчивающийся в точке на внешней окружности с координатой
Находится пересечение этого отрезка с окружностью равного КБВ, на которой располагается точка А. Это пересечение обозначаем как точка В (см. рис.3). Точка В и есть пересчитанное значение сопротивления z1 в сторону к генератору на расстояние . Назовем это сопротивление z2
По круговой диаграмме определяем численные значения активной и реактивной части сопротивления точки В. Как видно из рис.3 точка В лежит на пересечении окружности r=r2 и дуги x=x2. Соответственно, сопротивление z2= r2 +ix2
Таким образом, если известно хотя бы одно эквивалентное сопротивление (проводимость) в каком-либо сечении линии, с помощью круговой диаграммы легко найти эквивалентное сопротивление (проводимость) в любом другом сечении. Как правило, сначала определяют сопротивление нагрузки, т. е эквивалентное сопротивление в сечении z=0. Для этого производят два опыта, структурная схема, которых показана на рис.4
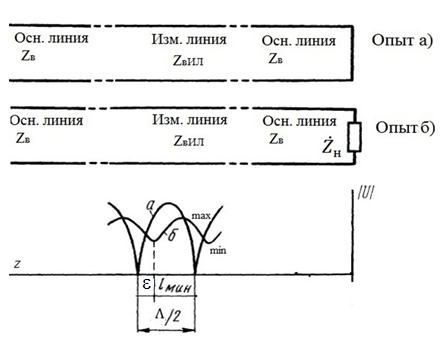
Рис.4
В
опыте короткого замыкания (опыт а)
определяется положение двух соседних
узлов амплитуды напряжения, находящегося
в пределах рабочего участка измерительной
линии и таким образом измеряется длина
волны
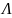 . Далее подключается нагрузка (опыт б)
и определяется отношение минимальной
к максимальной амплитуды напряжения -
КБВ, а также местоположение одного,
абсолютно любого, минимума напряжения
находящегося в пределах рабочего участка
измерительной линии. После этого
определяется смещение узла в опыте б)
относительно любого из двух найденных
в опыте а) узлов напряжения -
. Далее подключается нагрузка (опыт б)
и определяется отношение минимальной
к максимальной амплитуды напряжения -
КБВ, а также местоположение одного,
абсолютно любого, минимума напряжения
находящегося в пределах рабочего участка
измерительной линии. После этого
определяется смещение узла в опыте б)
относительно любого из двух найденных
в опыте а) узлов напряжения -
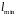 или
или
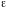 .
Как правило, величина смещения определяется
меньшой среди величин
или
.
На рис.4 это величина
.
Поскольку
нормированное сопротивление в узле при
опыте КЗ равно 0, что совпадает с нагрузкой
опыта а), делается вывод что расстояние
от нагрузки до узла опыта а) равняется
целому числу полуволн. Тогда нормированное
сопротивление в том же самом сечении,
но уже при опыте б) будет равно
нормированному сопротивлению нагрузки
и следовательно необходимо пересчитать
нормированное сопротивление из минимума
напряжения в опыте б) в то сечение где
в опыте КЗ был узел напряжения, т.е. на
величину
.
Так
как эквивалентное нормированное
сопротивление в узле амплитуды напряжения
чисто активно и равно КБВ [2,3] ,
то
нормированное сопротивление нагрузки
может быть определено как
.
Как правило, величина смещения определяется
меньшой среди величин
или
.
На рис.4 это величина
.
Поскольку
нормированное сопротивление в узле при
опыте КЗ равно 0, что совпадает с нагрузкой
опыта а), делается вывод что расстояние
от нагрузки до узла опыта а) равняется
целому числу полуволн. Тогда нормированное
сопротивление в том же самом сечении,
но уже при опыте б) будет равно
нормированному сопротивлению нагрузки
и следовательно необходимо пересчитать
нормированное сопротивление из минимума
напряжения в опыте б) в то сечение где
в опыте КЗ был узел напряжения, т.е. на
величину
.
Так
как эквивалентное нормированное
сопротивление в узле амплитуды напряжения
чисто активно и равно КБВ [2,3] ,
то
нормированное сопротивление нагрузки
может быть определено как
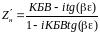 ,
(5)
,
(5)
где знак “-“ указывает что направление пересчета противоположно направлению смещения . Наиболее просто определение нормированного сопротивления нагрузки, как частный случай использования формулы пересчета, может быть проведено с помощью круговой диаграммы, как показано на рис.5
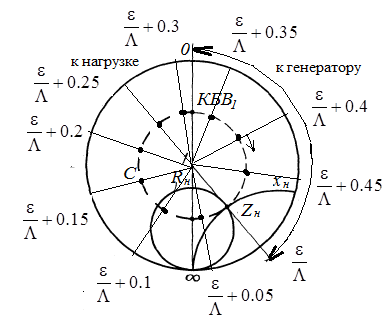
Рис.5
Допустим,
при подключении нагрузки узел амплитуды
напряжения сместился на величину
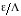 в
сторону к нагрузки, а величина КБВ
составила КБВ1.
Тогда для нахождения сопротивления
нагрузки и эквивалентных сопротивлений,
в сечениях отстоящих от нагрузки на
заданное расстояние, необходимо выполнить
следующие операции, схематично показанные
на рис.5
в
сторону к нагрузки, а величина КБВ
составила КБВ1.
Тогда для нахождения сопротивления
нагрузки и эквивалентных сопротивлений,
в сечениях отстоящих от нагрузки на
заданное расстояние, необходимо выполнить
следующие операции, схематично показанные
на рис.5
Поскольку узел в режиме подключения нагрузки сместился в сторону к нагрузке относительно опыта КЗ, а пересчет сопротивления производится из узла в режиме подключения нагрузки в узел опыта КЗ (см. рис.4) на круговой диаграмме в сторону противоположную смещению узла, в нашем примере в сторону генератора, по внешнему кругу откладывается величина (см. рис.5)
Из центра круговой диаграммы в точку отложенную на внешнем круге в п.1 проводится отрезок. Также на круговой диаграмме находится пунктирная окружность постоянного КБВ=КБВ1. Пересечение этой окружности и отрезка и есть точка сопротивления нагрузки Zн
Для нахождения эквивалентных сопротивлений с шагом 0.05 , как требуется в задании к расчетной части из центра круговой диаграммы в сторону к генератору проводятся вспомогательные отрезки соединяющие центр круговой диаграммы и точки на внешнем круге с координатами
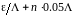 ,
где
,
где
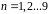 .
Полученные точки пересечения этих
отрезков с пунктирной окружностью
постоянного КБВ=КБВ1
и есть эквивалентные сопротивления в
соответствующем сечении (см. рис.5).
Например, точка С на рис.5 соответствует
эквивалентному сопротивлению в сечении
отстоящим от нагрузки на
.
Полученные точки пересечения этих
отрезков с пунктирной окружностью
постоянного КБВ=КБВ1
и есть эквивалентные сопротивления в
соответствующем сечении (см. рис.5).
Например, точка С на рис.5 соответствует
эквивалентному сопротивлению в сечении
отстоящим от нагрузки на
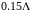 .
.Полученные значения сопротивления нагрузки и эквивалентных сопротивлений объединяются в одну таблицу, после чего строится график, согласно требованиям п.3.2
П.3 КОМПЕНСАЦИОННЫЙ МЕТОД НАСТРОЙКИ ЛИНИИ В РЕЖИМ БЕГУЩЕЙ ВОЛНЫ
Существует несколько методов согласования нагрузки с Zв линии [1-3]. В данной лабораторной работе используется метод, предложенный Татариновым [2,3]. Идея метода состоит в следующем. Если линия нагружена на сопротивление, не равное Zв, появится отраженная волна. При правильном выборе места включения и величины реактивного сопротивления (проводимости) этого элемента поля отраженной от него волны будет равно по амплитуде и противоположно по фазе, поля отраженному от нагрузки. В результате отраженные волны скомпенсируют друг друга (отсюда и название метода) и в линии от генератора до места включения согласующего элемента будет только бегущая волна.
Идею
настройки линии в режим бегущей волны
можно объяснить также пользуясь понятиями
эквивалентных сопротивлений и
проводимостей. Эквивалентная нормированная
проводимость линии Y’(z)=1/Z’(z)=g(z)+ib(z)
согласно (2) представляет собой
периодическую функцию с периодом
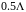 .
Как видно из рис.6 на протяжении половины
длины волны существуют два сечения в
линии, где активная часть нормированной
проводимости g(z)=1.
В сечении “А” эквивалентная
проводимость линии имеет емкостной
характер (b1>0),
а в сечении “Б” индуктивный (b2<0).
Если в сечении “1”включить параллельно
чисто индуктивное сопротивление c
отрицательной проводимостью -b1,
то суммарная проводимость в сечении
“A” будет чисто активной
и равной 1 (g1=1).
Тогда на участке от генератора до места
включения реактивности будет только
бегущая волна. Аналогично можно добиться
настройки линии в режим бегущей волны
и в сечении “Б”, где согласующий элемент
должен иметь емкостное сопротивление.
.
Как видно из рис.6 на протяжении половины
длины волны существуют два сечения в
линии, где активная часть нормированной
проводимости g(z)=1.
В сечении “А” эквивалентная
проводимость линии имеет емкостной
характер (b1>0),
а в сечении “Б” индуктивный (b2<0).
Если в сечении “1”включить параллельно
чисто индуктивное сопротивление c
отрицательной проводимостью -b1,
то суммарная проводимость в сечении
“A” будет чисто активной
и равной 1 (g1=1).
Тогда на участке от генератора до места
включения реактивности будет только
бегущая волна. Аналогично можно добиться
настройки линии в режим бегущей волны
и в сечении “Б”, где согласующий элемент
должен иметь емкостное сопротивление.
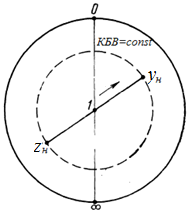
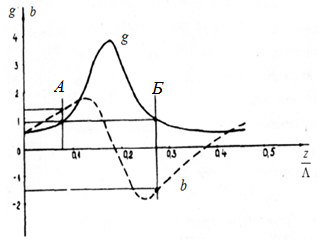
Рис.6 Рис.7
Положение
сечений “А” и “Б” и проводимости
согласующих элементов находится по
круговой диаграмме следующим образом.
Поскольку в этом методе согласующий
элемент включается в линию параллельно
удобнее пользоваться понятиями
эквивалентных проводимостей, поэтому
необходимо по заданному нормированному
сопротивлению нагрузки Zн
найти нормированную проводимость
Yн. Для этого
на круговой диаграмме откладывается
точка Zн по
правилам описанным в приложении 2. Затем
через эту точку проводится пунктирная
окружность КБВ=const.
Отрезок, соединяющий центр круговой
диаграммы и точку Zн,
поворачивается на 1800, что
соответствует пересчету на
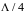 по круговой диаграмме. Точка пересечения
зеркального отрезка и пунктирной
окружности и есть Yн.
Вся процедура нахождения Yн
схематично показана на рис.7
по круговой диаграмме. Точка пересечения
зеркального отрезка и пунктирной
окружности и есть Yн.
Вся процедура нахождения Yн
схематично показана на рис.7
На
рис.8 показано нахождение место включения
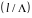 согласующего элемента и определение
величин проводимости согласующих
элементов при его включении в сечение
“А” и “Б” с помощью круговой диаграммы.
согласующего элемента и определение
величин проводимости согласующих
элементов при его включении в сечение
“А” и “Б” с помощью круговой диаграммы.
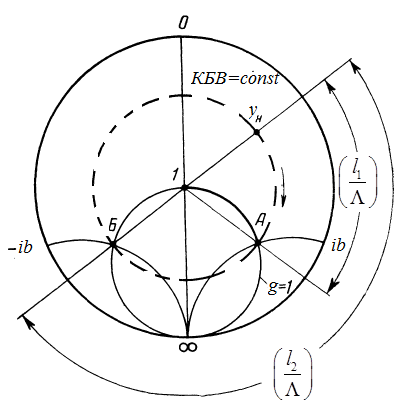
Рис.8
Поскольку
активная проводимость линии путем
параллельного включения реактивного
согласующего элемента изменена быть
не может, очевидно что согласующий
элемент может быть помещен только в то
сечение линии, где нормированная активная
проводимость линии равна 1. На круговой
диаграмме имеется две точки (А и Б)
пересечения пунктирной окружности
КБВ=const c
окружностью равных активных проводимостей
g=1. Расстояние от
нагрузки до точки А
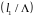 определяется на внешнем круге по часовой
стрелке, поскольку согласующее устройство
включается перед нагрузкой, т.е. ближе
к генератору. Аналогично определяется
и расстояние до точки Б
определяется на внешнем круге по часовой
стрелке, поскольку согласующее устройство
включается перед нагрузкой, т.е. ближе
к генератору. Аналогично определяется
и расстояние до точки Б
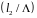 .
При включении согласующего элемента в
сечение “А” его реактивная проводимость
должна компенсировать реактивную
проводимость линии в точке А. Как мы
видим по рис.8 реактивная проводимость
в точке А положительна (
.
При включении согласующего элемента в
сечение “А” его реактивная проводимость
должна компенсировать реактивную
проводимость линии в точке А. Как мы
видим по рис.8 реактивная проводимость
в точке А положительна (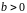 )
поэтому согласующий элемент должен
иметь отрицательную реактивность
)
поэтому согласующий элемент должен
иметь отрицательную реактивность
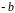 ,
что соответствует индуктивной диафрагме.
При включении согласующего элемента в
сечение “Б” реактивная проводимость
отрицательна, поэтому наш согласующий
элемент должен иметь положительную
проводимость (
),
что соответствует емкостному штырю.
,
что соответствует индуктивной диафрагме.
При включении согласующего элемента в
сечение “Б” реактивная проводимость
отрицательна, поэтому наш согласующий
элемент должен иметь положительную
проводимость (
),
что соответствует емкостному штырю.

П.4 КРУГОВАЯ ДИАГРАММА ПОЛНЫХ СОПРОТИВЛЕНИЙ (см. вклейку)
