ЧМ6Стецкий

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра "Информатика"

ОТЧЁТ

по дисциплине "Численные методы"

на тему:

"Лабораторная работа №6.

Одномерная оптимизация"

Выполнил студент

Группы БИК2209

Стецкий Н.С.

Вариант 23

Преподаватель:

СОДЕРЖАНИЕ

Лабораторная работа № 6.

"Одномерная оптимизация"

Вариант 23

1. Задание:

Таблица 1 – Задание по варианту

№	Уравнение
23

Ручной расчет: метод дихотомии

Решение программой: метод золотого сечения

Цель работы:

Выяснить, какой метод из представленных является наиболее оптимальным по точности по числу итераций.

2. Исследование задания:

График функции :

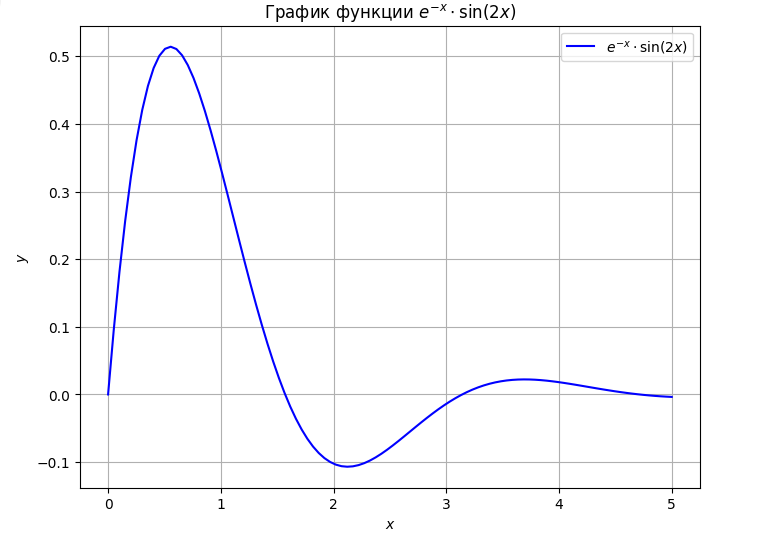
Рисунок 1 – График функции y=f(x)

Так как функция на интервале экспоненциально увеличивает амплитуду, то рассматривать будем функцию на неотрицательных значениях. Выберем по построенному графику функции начальный отрезок неопределенности (отрезок, содержащий точку минимума): отрезок [1.9; 2.4].

Рисунок 2 – График функции на отрезке, содержащим точку минимума

Проверка выполнения аналитического условия унимодальности функции на выбранном отрезке:

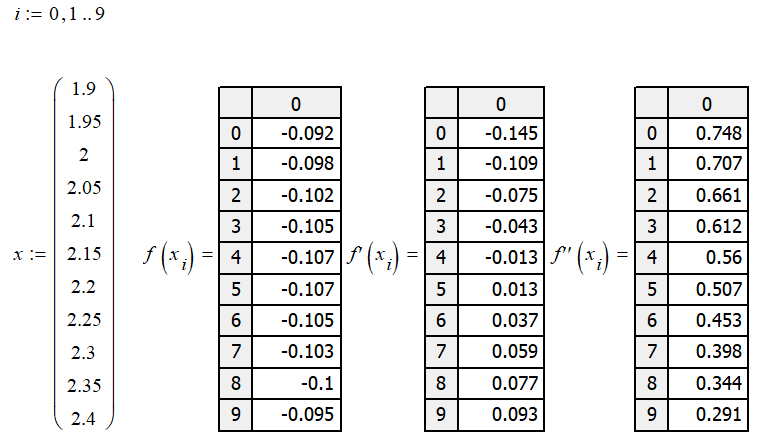
Приведенные выше расчеты подтверждают, что на отрезке [1.9; 2.4] функция f(x) является унимодальной, так как выполняются следующие условия:

1. Производная на отрезке [1.9; 2.4] монотонна по обе стороны от минимума (сначала убывает, достигнув минимума, начинает возрастать).

2. 

3. Ручной расчет методом дихотомии

Результаты расчетов занесены в таблицу 2:

Таблица 2

n	a	b	x1	x2	f(x1)	f(x2)	∆n
1	1.9	2.4	2.1475	2.1525	-0.10675	-0.10668	0.2525
2	1.9	2.1525	2.02375	2.02875	-0.10401	-0.10429	0.12875
3	2.02375	2.1525	2.08562	2.09062	-0.10648	-0.10658	0.06688
4	2.08562	2.1525

Вывод: Для метода дихотомии длина отрезка неопределенности после трех итераций ∆_n = 0.0668 За минимум была принята середина оставшегося отрезка x_min = 2.11906, а y(x_min) = -0.10688.

4. Число итераций, необходимых для локализации точки минимума и Е=10^-4 для метода дихотомии

Теоретическая величина погрешности для метода дихотомии определяется длиной конечного отрезка неопределенности после N итераций: . Отсюда, принимая во внимание, что , можно определить соответствующее число итераций:

Если точность Е=0.0001, а параметр метода d=0.01 получим:

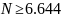, следовательно, N = 7

Вывод: для достижения точности 10^-4 методом дихотомии нужно выполнить 7 итераций.

4. Метод золотого сечения

Вывод программы:

Вывод: для нахождения точки минимума с точностью 10^-4 методом золотого сечения понадобилось 18 итераций. x_min = 2.1243684207, а y(x_min) = -0.106891341. Длина отрезка неопределенности ∆_n = 1.497*10^-8.

4. Число итераций, необходимых для локализации точки минимума и Е=10^-4 для метода золотого сечения

Теоретическая величина погрешности для метода золотого сечения определяется длиной конечного отрезка неопределенности после N итераций , где a = 1.9, b = 2.4. Отсюда имеем ,

N = 18

Вывод: для достижения точности 10^-4 методом золотого сечения нужно выполнить 18 итераций, что совпадает с выводом, полученным в результате выполнения программы.

4. Решение с использованием функции пакета MathCad

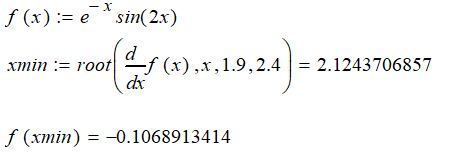
4. Выводы

После трех итераций, выполненных методом дихотомии, минимум составил: x_min = 2.11906, а y(x_min) = -0.10688. Для достижения точности 10^-4 методом дихотомии нужно выполнить 7 итераций.

Для нахождения точки минимума с точностью 10^-4 методом золотого сечения понадобилось 18 итераций. x_min = 2.1243684207, а y(x_min) = --0.106891341.

Точное решение, полученное с помощью функции Mathcad составило x_min = 2.12437, f(x_min) = -0.10689

2024