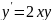ЧМ5Стецкий

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра "Информатика"

ОТЧЁТ

по дисциплине "Численные методы"

на тему:

"Лабораторная работа №5.

Методы решения обыкновенных дифференциальных уравнений"

Выполнил студент

Группы БИК2209

Стецкий Н.С.

Вариант 23

Преподаватель:

СОДЕРЖАНИЕ

Лабораторная работа № 5.

"Методы решения обыкновенных дифференциальных уравнений"

Вариант 23

1. Задание:

Таблица 1 – Задание по варианту

№	Уравнение	x0	y0	h0	a	b
23		0	1	0.2	0	0.6

Цель работы:

Решить обыкновенное дифференциальное уравнение аналитически, методом Эйлера и методом Рунге-Кутта 4-то порядка.

2. Аналитическое решение

Найдем точное аналитическое решение заданного дифференциального уравнения, для этого запишем уравнение в виде 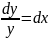и проинтегрируем:

Вывод: Найдено точное аналитическое решение заданного дифференциального уравнения: _.

3. Значения точного решения ОДУ

Вычислим значения полученного решения 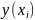на отрезке [0; 0.6] с шагом изменения аргумента 0.2:

Таблица 1 – Значения точного решения ОДУ

xi	y(xi)
0	1
0.2	1.04081
0.4	1.17351
0.6	1.43333

4. Численное решение заданного ОДУ методом Эйлера

Вычислим значения численного решения ОДУ методом Эйлера ( ) в точках отрезка [0; 0.6] с шагом h = 0.2. Для этого ОДУ записывают в виде 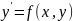. Общая формула для определения очередного значения функции по методу Эйлера имеет вид , где :

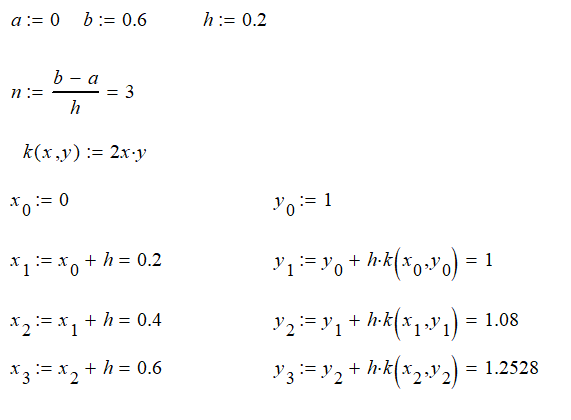
Таблица 2 – Результаты численного решения ОДУ методом Эйлера

xi
0	1
0.2	1
0.4	1.08
0.6	1.2528

5. Значения погрешностей метода Эйлера

Вычислим значения погрешностей по формуле :

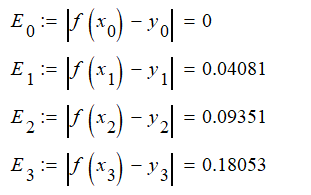
Таблица 3 – Погрешности решения ОДУ методом Эйлера

xi
0	0
0.2	0.04081
0.4	0.09351
0.6	0.18053

6. Решение ОДУ методом Рунге-Кутта 4-го порядка

Вычислим с помощью программы значения численного решения ОДУ с точностью 10^-4, и получим решение в точках отрезка [0; 0.6] с шагом h = 0.2 (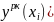 методом Рунге-Кутта 4-го порядка с автоматическим выбором шага, используя формулы:

,

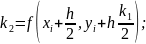
Был реализован программный код, листинг которого представлен на Рисунке 1.

Рисунок 1

После запуска программы были получены результаты, представленные на Рисунке 2.

Рисунок 2

Вывод: Получено численное значение ОДУ с точностью 10^-4 методом Рунге-Кутта 4-го порядка с автоматическим выбором шага: y(x) = 1.4333. Шаг обеспечивающий заданную точность составил 0.025, количество разбиений интервала m = 8.

7. Значения погрешностей решения методом Рунге-Кутта 4-го порядка

Вычислим значения погрешностей по формуле: .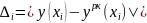

Таблица 4 – Погрешности решения ОДУ методом Рунге-Кутта

xi
0	0
0.2
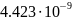
0.4
0.6

8. Решение с использованием функции пакета MathCad

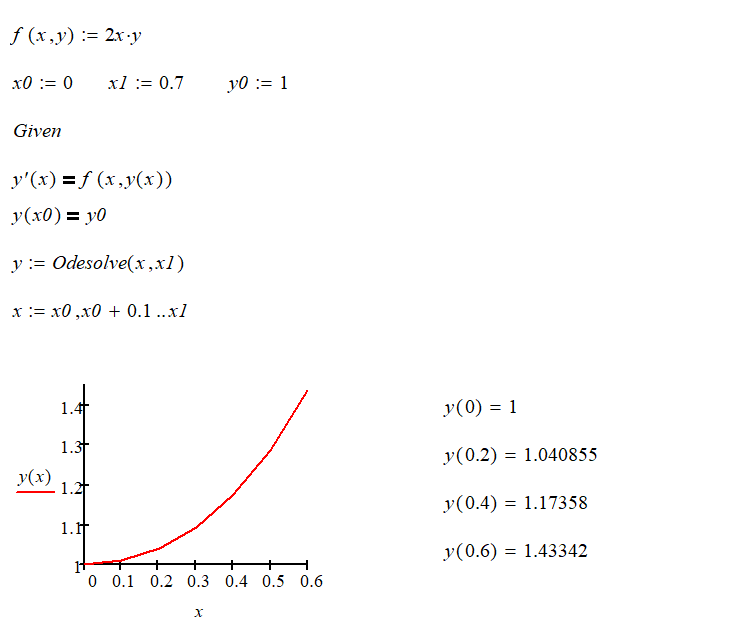
9. Выводы

Все решения, полученные выше, сведем в таблицу 5.

Таблица 5 – Таблица результатов

xi	y(xi)
0	1	1	0	1	0	1
0.2	1.04081	1	0.04081	1.0408107		1.040855
0.4	1.17351	1.08	0.09351	1.1735108		1.17358
0.6	1.43333	1.2528	0.18053	1.4333294		1.43342

y(x_i) – аналитическое решение ОДУ,

– решение ОДУ методом Эйлера,

– решение ОДУ методом Рунге-Кутты 4-го порядка,

– решение ОДУ с использованием функции Mathcad

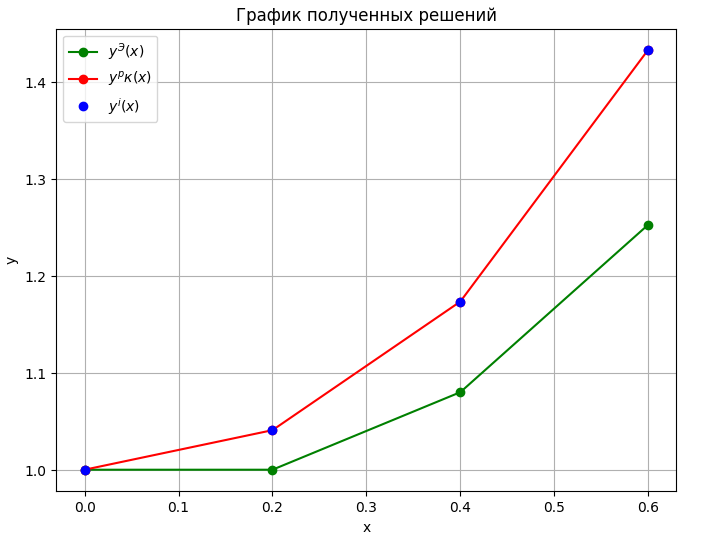
Рисунок 2 – График полученных решений

2024