ЧМ3Стецкий

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра "Информатика"

ОТЧЁТ

по дисциплине "Численные методы"

на тему:

"Лабораторная работа №3.

Метод наименьших квадратов"

Выполнил студент

Группы БИК2209

Стецкий Н.С.

Вариант 23

Преподаватель:

СОДЕРЖАНИЕ

Лабораторная работа № 3.

"Метод наименьших квадратов"

Вариант 23

1. Задание:

Таблица 1 – Задание по варианту

№ варианта	Функция из табл. 1-2	Номера узлов из табл. 1-2
23	f2	11,12,13,14,15,16,17

Цель работы:

Выполнить линейную аппроксимацию:

- составить систему нормальных уравнений и решить её;

- вычислить значения аппроксимирующих функций в узловых точках и сравнить их со значениями исходной функции;

- вычислить среднеквадратичную погрешность (СКО).

2. Линейная аппроксимация

Для решения задачи аппроксимации методом наименьших квадратов выберем функцию y(x), заданную следующей таблицей:

Таблица 2

xi	-0.5	-0.4	-0.3	-0.2	-0.1	0	0.1
yi	-1.116	-1.206	-0.91	-0.326	0.376	1	1,376

Вычислим и запишем значения элементов матрицы Грамма и столбец свободных в таблицу 3.

Таблица 3

i	xi	yi	xi * yi	xi2
0	-0.5	-1.116	0.558	0,25
1	-0.4	-1.206	0.4824	0,16
2	-0.3	-0.91	-0.273	0,09
3	-0.2	-0.326	-0.0652	0,04
4	-0.1	0.376	-0.0376	0,01
5	0	1	0	0
6	0.1	1.376	1.1376	0,01
Σ	-1.4	-0.806	1.4786	0,56

Составим систему нормальных уравнений. Для линейной функции

P₁(x) = a₀ + a₁*x система нормальных уравнений примет вид (линейная аппроксимация):

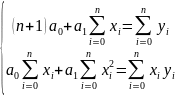
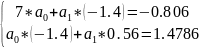
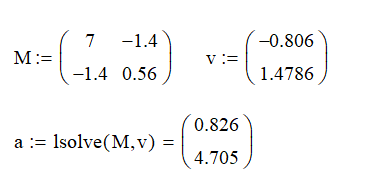
В результате решения системы уравнений получены коэффициенты a₀ = 0.826 и a₁ = 4.705.

Полином первой степени будет иметь вид: φ₁(x) = 0.826 + 4.705x.

Результаты аппроксимации в узловых точках, представленные в таблице:

Таблица 4

xi	-0.5	-0.4	-0.3	-0.2	-0.1	0	0.1
yi	-1.116	-1.206	-0.91	-0.326	0.376	1	1,376
φ1(xi)	-1,527	-1,056	-0,586	-0,115	0,356	0,826	1,297
yi – φ1(xi)	0,411	-0,15	-0,324	-0,211	0,02	0,174	0,079
(yi – φ1(xi))2	0,169	0,023	0,105	0,045	0	0,03	0,006

Проведем оценку погрешностей и вычислим среднеквадратичное отклонение:

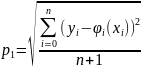= 0.232

Вывод: Получен полином первой степени φ₁(x) = 0.826 + 4.705x, среднеквадратичная погрешность которого составляет 0.232.

3. Аппроксимация с помощью математического пакета

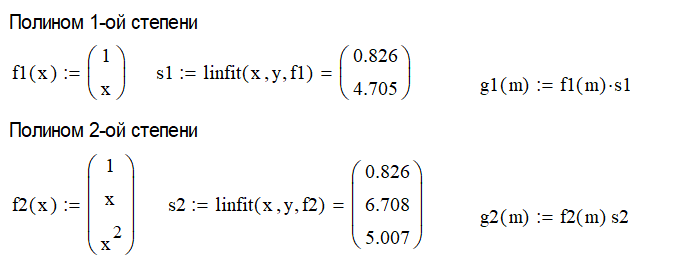
Вычислим среднеквадратичные отклонения для полиномов:

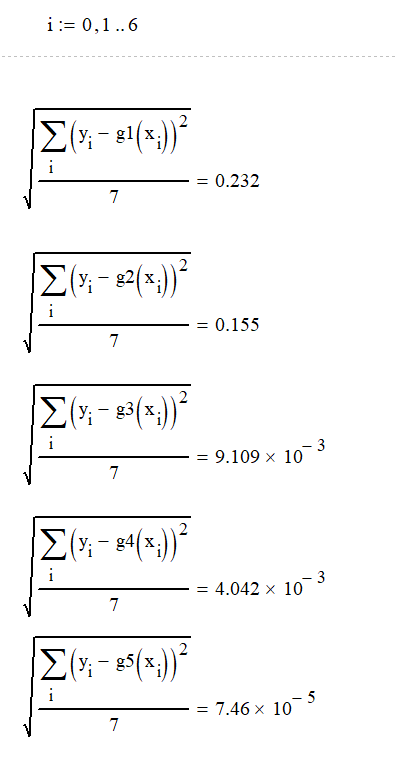
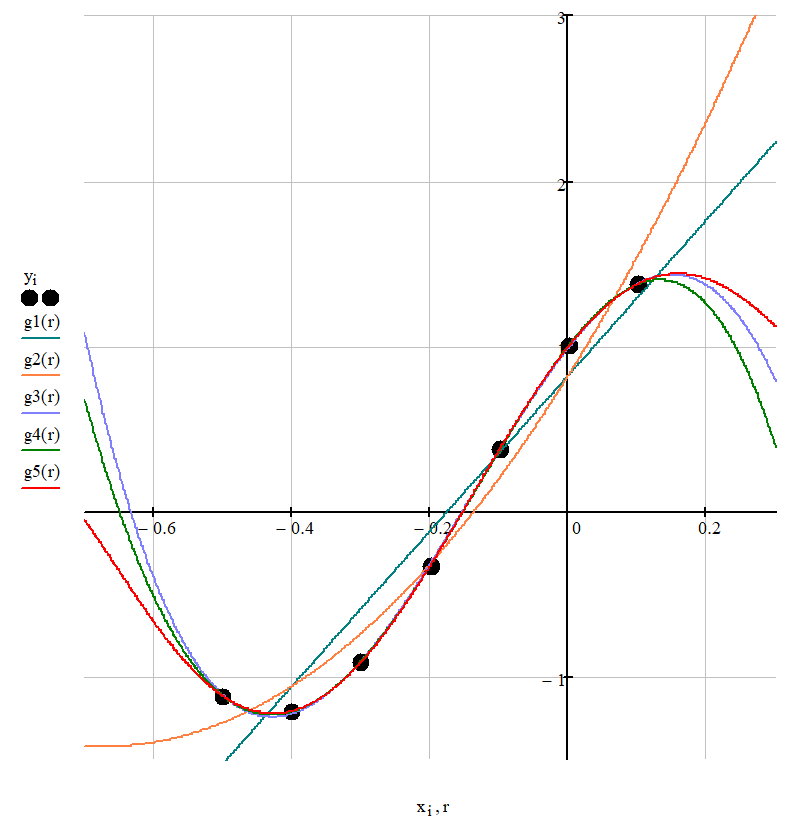
Рисунок 1 – График полученных результатов

Вывод: Проведена аппроксимация с помощью математического пакета Mathсad, в результате были получены полиномы 1, 2, 3, 4 и 5 степени и их среднеквадратичные отклонения, которые составляют 0.232 для полинома первой степени, 0.155 для полинома второй степени, 9.109*10^-3 для полинома третьей степени, 4.042*10^-3 для полинома четвертой степени и 7.46*10^-5 для полинома пятой степени. Полученные полиномы:

φ₁(x) = 0.826 + 4.705x

φ₂(x) = 0.826 + 6.708x + 5.007x²

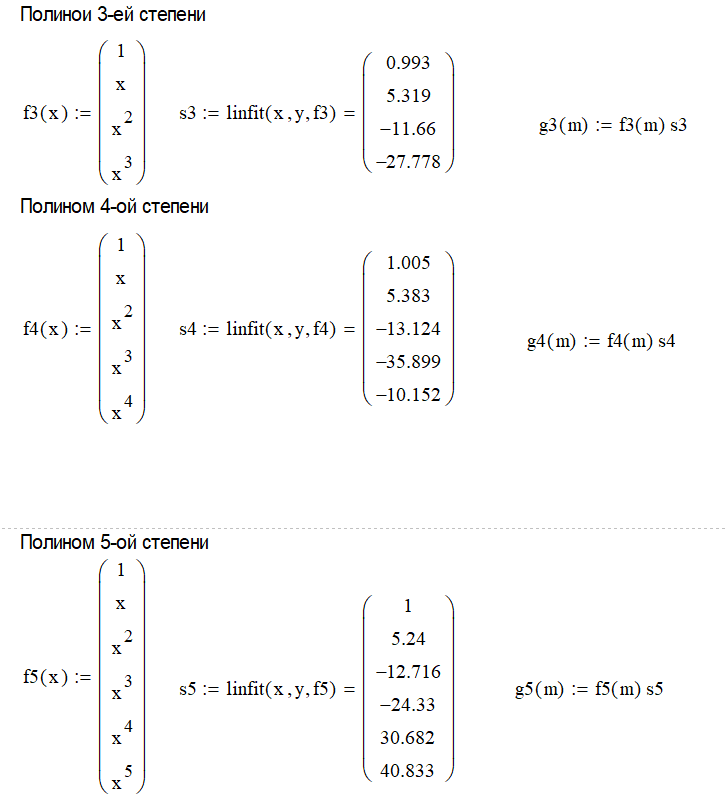
φ₃(x) = 0.993 + 5.319x - 11.66x² – 27.778x³

φ₄(x) = 1.005 + 5.383x - 13.124x² – 35.899x³ – 10.152x⁴

φ₅(x) = 1 + 5.24x -12.716x² - 24.33x³ + 30.682x⁴ + 40.833x⁵

2024