ЧМ2Стецкий

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра "Информатика"

ОТЧЁТ

по дисциплине "Численные методы"

на тему:

"Лабораторная работа №2.

Интерполяция функций"

Вариант 23.

Выполнил студент

Группы БИК2209

Стецкий Н.С.

Вариант 23

Проверил:

СОДЕРЖАНИЕ

Лабораторная работа № 2.

"Интерполяция функций"

Вариант 23

1. Задание:

x = a = 0.48 для интерполяции полиномом Ньютона

x = b =0.81 для интерполяции полиномом Лагранжа

Цель работы: провести интерполяцию функций в заданных точках полиномом Ньютона и полиномом Лагранжа.

2. Интерполяция в заданной точке с использованием Полинома Ньютона

Точка интерполяции для полинома Ньютона a = 0.48.

2.1 Выбор и нумерация узлов

Для ручной интерполяции в точке x = a = 0.48 по 1 формуле Ньютона выбираем 4 узла из таблицы 1–2 так, чтобы точка a = 0.48 оказалась между узлами с номерами с 8 по 9 и добавляем узлы вправо:

Таблица 1 – Узлы, взятые из таблицы 1-2 из дано

Номера выбранных узлов (k)	xk	yk
8	0.45	-3.4890
9	0.50	-3.3250
10	0.55	-3.1385
11	0.60	-2.9280

Выбор точек определяется тем, чтобы при решении задачи интерполяции в точке по первой формуле Ньютона, точка должна быть внутри таблицы для полинома любой степени, в том числе и первой. Поэтому нулевой и первый узел должны находиться по разные стороны от самой точки x=a.

Так как нулевой узел находится слева от точки, а первый узел находится справа от точки, то шаг h=x₁-x₀ будет положительным и добавлять узлы следует справа относительно точки x=0.48.

Переномеруем узлы и занесем их в таблицу:

Таблица 2 – Узлы, которые будем использовать для интерполяции полиномом Ньютона

k	0	1	2	3
xk	0.45	0.50	0.55	0.60
yk	-3.4890	-3.3250	-3.1385	-2.9280

2.2 Вычислим конечные разности и заполним таблицу:

∆y₀ = y₁ – y₀ = -3.3250 – ( -3.4890) = 0.1640

∆y₁ = y₂ – y₁ = -3.1385 – (-3.3250) = 0.1865

∆y₂ = y₃ – y₂ = -2.9280 – (-3.1385) = 0.2105

∆²y₀ = ∆y₁ – ∆y₀ = 0.1865 - 0.1640 = 0.0225

∆²y₁ = ∆y₂ – ∆y₁ = 0.2105 - 0.1865 = 0.0240

∆³y₀ = ∆²y₁ – ∆²y₀ = 0.0240 - 0.0225 = 0.0015

Таблица 3 – Таблица конечных разностей для интерполяционной формулы Ньютона

x	y	∆y	∆2y	∆3y
0.45	-3.4890	0.1640	0.0225	0.0015
0.50	-3.3250	0.1865	0.0240
0.55	-3.1385	0.2105
0.60	-2.9280

Запишем 1–ю интерполяционную формулу Ньютона:

2.3 Выполним расчеты для полиномов 1-й, 2-й и 3-й степени:

Определим значение q:

Значение полинома 1-й степени в точке x = 0.48:

-3.4890 + 0.1640 * 0.6 = -3.3906

Значение полинома 2-й степени в точке x = 0.48:

- 3.3879

Значение полинома 3-й степени в точке x = 0.48:

Явные выражения для полиномов 1, 2 и 3 степени могут быть получены после соответствующих преобразований формулы:

Вычислим оценки погрешности в точке x=0.48 для полиномов. Оценку погрешности проведём в соответствии с неравенством:

|f(x) – P_n(x)| ≤ |P_n+1(x) – P_n(x)

|- 3.3879– (-3.3906) | = 0.0027

|-3.3878 – (-3.3879) | = 0.0001

Занесем результаты в таблицу 4:

Таблица 4 – Результаты интерполяции полнимом Ньютона

Степень многочлена k	Pk(x)	Оценка погрешности
1	-3.3906	0.0027
2	- 3.3879	0.0001
3	-3.3878	_

Таблица 5

k	0	1	2	3
xk	0.45	0.50	0.55	0.60
yk	-3.4890	-3.3250	-3.1385	-2.9280
P1	-3.489	-3.325	-3.161	-2.997
P2	-3.489	-3.325	-3.1385	-2.9295
P3	-3.489	-3.325	-3.1385	-2.9280

Вывод. Получены выражения для интерполяционных многочленов 1, 2 и 3-ей степени и их значения в точке а = 0.48 (P₁(x) = -3.3906; P₂(x) = -3.3879; P₃(x) = -3.3878). Проведена оценка погрешности: Разность между точным (неизвестным) значением функции и значением интерполяционного полинома в точке x=0.48 после 3-х итераций не превышает 0.0001.

3. Интерполяция в заданной точке с использованием полинома Лагранжа

x = b =0.81 для интерполяции полиномом Лагранжа

3.1 Выбор и перенумерация узлов

Для ручной интерполяции в точке x = b = 0.81 по формуле Лагранжа выбираем из таблицы 1–2 4 узла так, чтобы точка b = 0.81 оказалась внутри получающийся таблицы и узлы были наиболее близкими к этой точке. В итоге выбираем узлы с номерами 16, 17, 18, 18:

Таблица 5 – Узлы, взятые из таблицы 1-2 из дано

n	xn	yn
14	0.75	-2.1375
15	0.8	-1.816
16	0.85	-1.463
17	0.9	-1.077

Перенумеруем узлы интерполяции так, чтобы точка x=0.81 была внутри таблицы и узлы ближайшие к ней. Занесем перенумерованные узлы в таблицу 6.

Таблица 6 – Узлы, которые будем использовать интерполяции полиномом Лагранжа

k	0	1	2	3
xk	0.8	0.85	0.75	0.90
yk	-1.816	-1.463	-2.1375	-1.077

3.2 Вычисление интерполяционных полиномов

Запишем интерполяционные формулы для полиномов Лагранжа 1–й, 2–й и 3–й степени и вычислим их значения в точке x = 0.81:

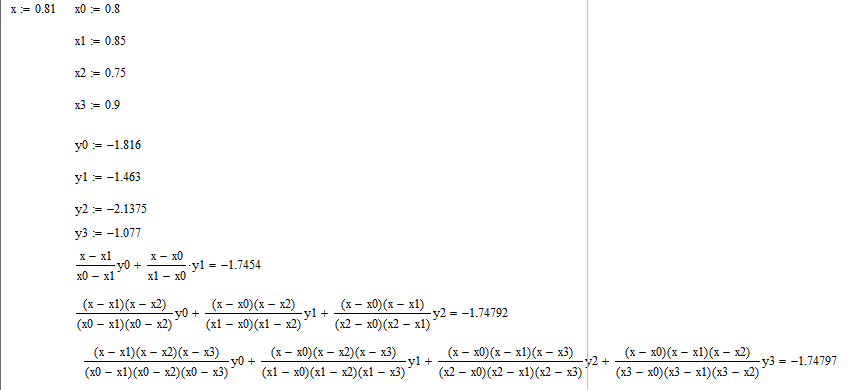
Рисунок 1 – Интерполяционные формулы для полиномов Лагранжа

Вычислим оценки погрешности в точке x=0.81 для полиномов. Оценку погрешности проведём в соответствии с неравенством:

|f(x) – L_n(x)| ≤ |L_n+1(x) – L_n(x)

|-1.7454 – (-1.74792)| = 0.00252

|-1.74792 – (-1.74797)| = 0.00005

Таблица 7 – Результаты интерполяции полнимом Лагранжа

Степень многочлена k	Lk(x)	Оценка погрешности
1	-1.7454	0.00252
2	-1.74792	0.00005
3	-1.74797	_

Таблица 8

k	0	1	2	3
xk	0.8	0.85	0.75	0.9
yk	-1.816	-1.463	-2.1375	-1.077
L1	-1.816	-1.463	-2.1690	-1.110
L2	-1.816	-1.463	-2.1375	-1.0785
L3	-1.816	-1.463	-2.1375	-1.077

Вывод. Получены выражения для интерполяционных полиномов 1, 2 и 3-ей степени и их значения в т. b=0.81 (L₁(x)=-1.7454; L₂(x)=-1.74792; L₃(x)= -1.74797). Проведена оценка погрешности - разность между точным (неизвестным) значением функции и значением интерполяционного полинома в точке x=0.81 после 3-х итераций не превышает 0.00005.

4. Общий вывод: Получены выражения для интерполяционных полиномов Ньютона 1, 2 и 3-ей степени и их значения в точке а= 0.48 (P₁(x) = -3.3906; P₂(x) = -3.3879; P₃(x) = -3.3878) и выражения для интерполяционных полиномов Лагранжа 1, 2 и 3-ей степени и их значения в точке b=0.81 (L₁(x)=-1.7454; L₂(x)=-1.74792; L₃(x)= -1.74797).

Проведена оценка погрешности для обоих случаев, в результате которой было выяснено, что разность между точным (неизвестным) значением функции и значением интерполяционного полинома Ньютона в точке a=0.48 после 3-х итераций не превышает 0.0001, а для полинома Лагранжа в точке b=0.81 после 3-х итераций разность не превышает 0.00005. Следовательно, интерполяция по первой формуле Ньютона является более быстрым способом, однако интерполяция формулой Лагранжа более точная.

2024