МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ»

Кафедра Информатики

Отчет по выполнению лабораторной работы №1

По дисциплине «Численные методы»

По теме «Методы решения нелинейных уравнений»

Выполнил студент

Группы БИК2209

Стецкий Н.С.

Вариант 23

Преподаватель:

Москва 2024

Содержание

Задание на лабораторную работу 3

Этап уточнения корня 5

Метод итераций 6

Метод Ньютона 7

Решение нелинейного уравнения средствами математического пакета 8

Выводы по итогам лабораторной работы 8

Задание на лабораторную работу

Решить уравнение: методами итераций и Ньютона.

Этап отделения корней

Отделение корней производилось графически. Результат представлен на рисунке 1.

Рисунок 1 – Графическое отделение корней

После графического отделения корней результат был подтвержден аналитически (Рисунок 2).

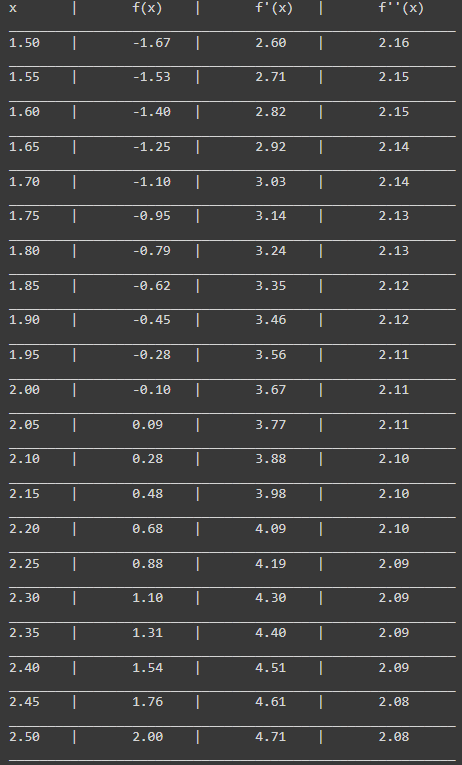
Рисунок 2 – Аналитическое подтверждение результата

На отрезке функция меняет знак, т.е. существует, по крайней мере, один корень. Поскольку знак первой производной на выбранном отрезке остается постоянным, можно сказать, что функция на выбранном отрезке монотонна. Знакопостоянство второй производной на выбранном отрезке является необходимым условием применения метода Ньютона и метода хорд. Следовательно, уравнение имеет единственный корень на отрезке .

Этап уточнения корня

Для начала выведем формулу

График данной формулы выглядит следующим образом:

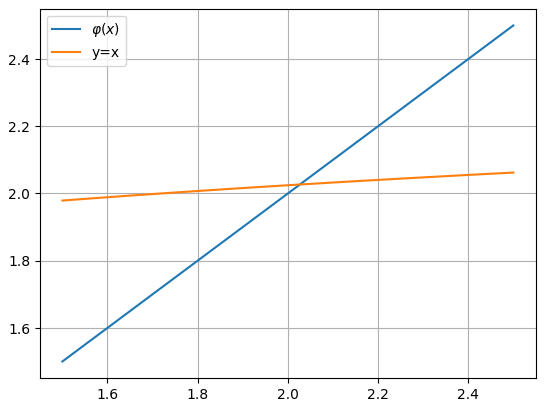
Рисунок 3 – Графическое изображение функции

Производная данной функции

Значения производной функции представлены на рисунке 4

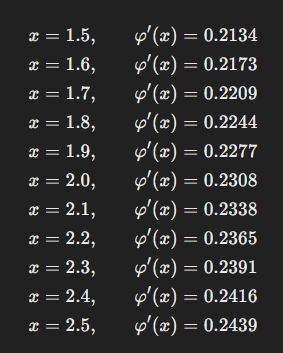
Рисунок 4 – Значения производной на интервале [1.5;2.5]

Видно, что на заданном интервале выполняется условие сходимости:

Метод итераций

Рисунок 5 – Ручной расчет методом простых итераций

Таким образом, результат уточнения корня при использовании метода половинного деления равен: . Для получения более точного результата следует увеличить количество итераций.

Метод Ньютона

Вычисления методом Ньютона проводились с применением языка python.

Для сходимости процесса необходим ряд условий, представленных на рисунке 6.

Рисунок 6 – условия сходимости метода Ньютона

Из результатов, полученных на рисунке 2 можем сделать выводы, представленные на рисунке 7

Рисунок 7 – выводы о сходимости метода Ньютона

Далее был реализован программный код на языке python, листинг которого представлен на Рисунке 8

Рисунок 8 – Тело программы

В результате его запуска были получены значения, представленные на Рисунке 9

Рисунок 9 – Результаты вычислений

Таким образом, результат вычисления методом Ньютона равен . Для получения большей точности следует увеличить количество итераций, изменив значение соответствующей переменной. При этом следует учитывать особенности хранения чисел с плавающей точкой. В языке python они хранятся с 18 знаками после запятой.

Решение нелинейного уравнения средствами математического пакета

Для решения НЛУ в математическом пакете Mathcad реализована функция Root. Ее применение представлено далее (Рисунок 10).

Рисунок 10 – Вычисление корня при помощи функции root

Выводы по итогам лабораторной работы

В ходе выполнения лабораторной работы применялись: метод простых итераций с ручным расчетом, метод Ньютона с расчетом при помощи алгоритма на языке python, встроенная в математический пакет функция вычисления корня уравнения.

При четырех итерациях точность метода итераций составила При этом точность при трех итерациях метода Ньютона составила