лаб 7 / цос лаба 7

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение

Кафедра радиотехнических систем

Лабораторная работа

по дисциплине

ЦИФРОВАЯ ОБРАБОТКА СИГНАЛА

«ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ. АЛГОРИТМ БЫСТРОГО ПРЕБРАЗОВАНИЯ ФУРЬЕ КУЛИ-ТЬЮКИ»

Выполнил:

студент группы БРВ2202

Стецкий Н.С.

Проверила:

Минаева О.Н.

Москва 2024

Цель работы:

Изучение дискретного преобразования Фурье и алгоритмов быстрого преобразования Фурье с прореживанием по времени и по частоте

Таблица 1. Исходные данные:

Переменная	Назначение	Формула	Значение
Nбр	Номер бригады	Nбр	20
N	Период (длина последовательности)	Т=1024
fД	Частота дискретизации	2000 (Nбр mod5+1)	2000
T	Период дискретизации	1/ fД	0,5 мс
A1	Амплитуды дискретных гармоник	A1=1+0,01 Nбр	1,2
A2		A2= 2A1	2,4
f1	Частота дискретной гармоники	f1= fд/8	250
f2	Частота дискретной гармоники	f2= fд/16	125

Последовательность x(n)=[01101110]

Или, для данной последовательности

Далее, учитывая, что k изменяется в интервале от 0 до N-1=7 рассчитаем коэффициенты ДПФ, применяя разложение экспоненты (поворачивающего множителя) по формуле Эйлера:

Для k=0

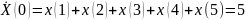
Так как значения равны между собой и равны единице, то при вычислении последующих коэффициентов ДПФ их запись можно опустить.

Для k=1

Для k=2

Для k=3

Для k=4

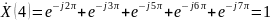
Для k=5

Для k=6

Для k=7

Расчёт коэффициентов ДПФ с помощью быстрого преобразования

Фурье с прореживанием по времени

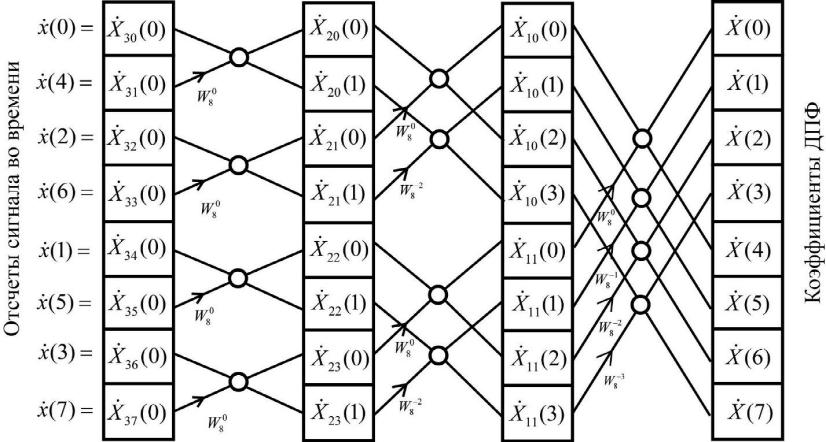Выполним алгоритм БПФ пошагово, пользуясь рисунком 1. Найдем коэффициенты

Поворачивающий множитель 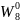равен единице.

Теперь, вычислим коэффициенты ДПФ последовательностей :

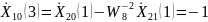
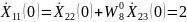
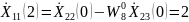
Последний шаг – нахождение коэффициентов ДПФ исходной последовательности x(n).

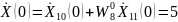
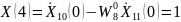
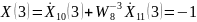
Значения коэффициентов ДПФ, посчитанные по общей формуле и по

алгоритму БПФ совпадают.

На этом расчет дискретного преобразования Фурье по алгоритму быстрого

преобразования Фурье окончен.

Расчёт коэффициентов ДПФ промежуточных последовательностей x₁₀(n) и x₂₀(n) по общей формуле. Сравнить результат с результатом, полученным при вычислении промежуточных последовательностей БПФ.

Рассчитаем по общей формуле коэффициенты ДПФ промежуточной

последовательности x₁₀(n), где x₁₀(n) - результат разбиения исходной

временной последовательности x(n) , включающий в себя только четные

коэффициенты x(n) ( нулевой, второй, четвертый и шестой): x₁₀(n) 0110 .

Длина последовательности x₁₀(n) N 4.

Для k=0

Для k=1

Для k=2

Для k=3

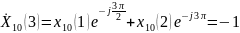
Последовательность имеет вид, который совпадает с результатами промежуточных вычислений БПФ.

Рассчитаем аналогичным образом коэффициенты ДПФ последовательности

, включающей в себя каждый второй член последовательности ,

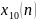начиная . Длина последовательности .

Выполнение:

Рисунок 1 – Система 1

Рисунок 2 – Система 2

Рисунок 3 – ДПФ одного гармонического сигнала

Рисунок 4 – ДПФ суммы

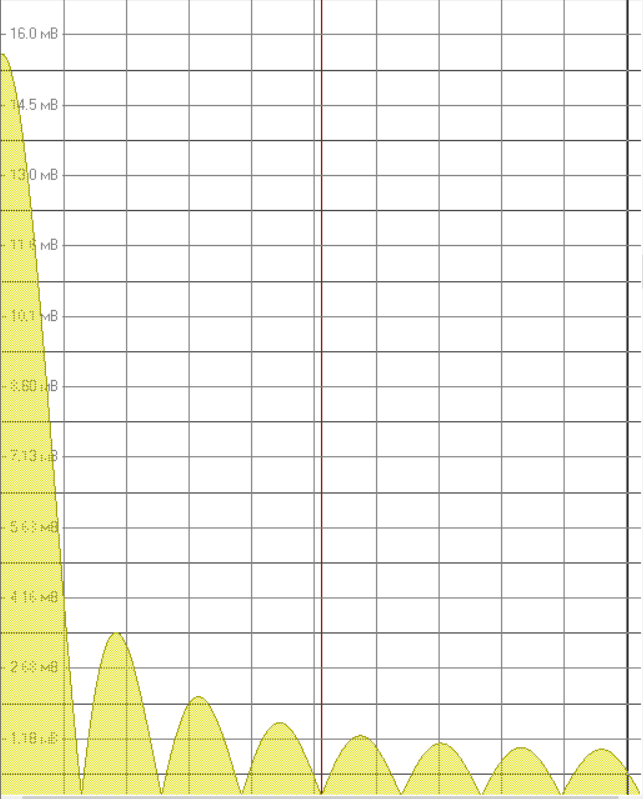
Рисунок 5 – график спектроанализатора

Рисунок 6 – график осциллографа

Вывод

В ходе лабораторной работы был изучен алгоритм БПФ Кули-Тьюки.