
лаб 2 / ЛАБА 1 ЦОС
.docxФедеральное агентство связи
Государственное образовательное учреждение высшего профессионального образования
Московский Технический Университет Связи и Информатики
(МТУСИ)
Кафедра радиотехнических систем
Лабораторная работа №2
ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК
ЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ
Выполнил
студент группы БРВ2202
Стецкий Н.С.
Проверил(а)
Цель работы:
Изучить математическое описание линейных дискретных систем (ЛДС) и овладеть программными средствами их моделирования и анализа в среде
«Спектр-2»
Переменная |
Назначение |
Значение |
Nбр |
Номер бригады |
20 |
b0 b1 b2 |
Коэфиценты числителя передаточной функции |
b0=0.9 b1=-1.2044 b2=0.72 |
a0 a1 a2 |
Коэфиценты знаменателя передаточной функции |
a0=1 a1=1.2778 a2=0.76 |
N1 |
Длина ИХ |
10 |
N2 |
Длина воздействия |
4 |
fд |
Частота дискретизации |
fд=20000 |
Домашний расчёт.
Домашний расчёт состоит из следующих пунктов:
Формирование основных характеристик линейной дискретной системы.
Определение устойчивости линейной дискретной системы.
Вычисление импульсной характеристики по разностному уравнению.
Вычисление импульсной характеристики по общей формуле.
Вычисление реакции линейной дискретной системы по формуле свёртки.
Вычисление реакции линейной дискретной системы по разностному уравнению.
Экспресс-анализ АЧХ и ФЧХ.
1.2 Формирование основных характеристик линейной дискретной системы второго порядка



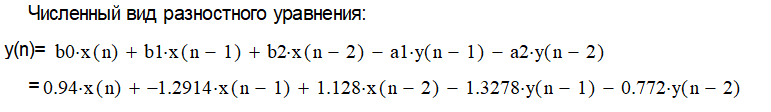

1.3 Определение устойчивости ЛДС.

Определяем полюсы:

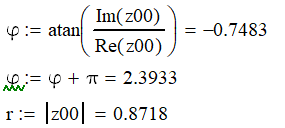
Определяем нули:
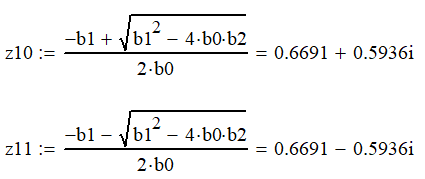
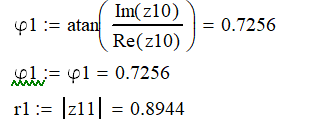
Строим нуль-полюсную диаграмму:

1.4 Вычисление импульсной характеристики по разностному уравнению.
Определение
отсчётов ИХ, при этом последовательность
на выходе ЛДС будет являться её импульсной
характеристикой



1.5 Вычисление импульсной характеристики по общей формуле для рекурсивного звена 2-го порядка с учётом нулевых начальных условий (ННУ).
Вычислим импульсную характеристику для ЛДС второго порядка по общей формуле, полученной из передаточной функции с помощью обратного z - преобразования:

Начиная с h(3) пользуемся этой формулой , так как все отсчёты воздействия будут равны нулю:
![]()
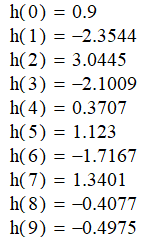
Вычисление реакции ЛДС по формуле свёртки.
В
качестве воздействия x(n)
примем прямоугольный импульс длины
 :
:
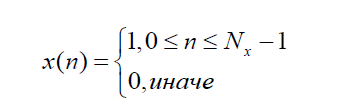
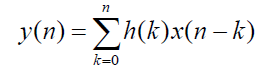
Общая длина выходного сигнала дискретной системы определяется как:
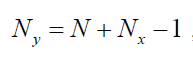
![]()
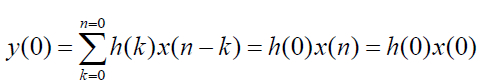
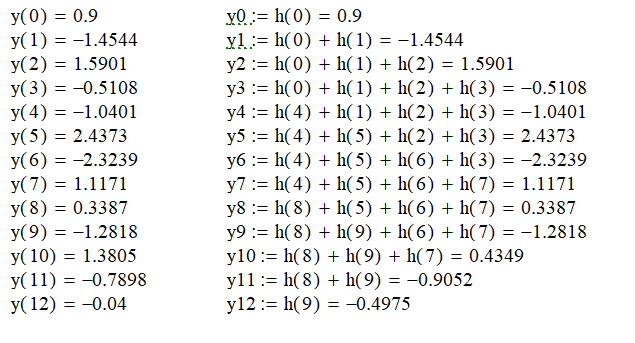
Вычисление реакции ЛДС по разностному уравнению.
Производится аналогично предыдущему пункту:
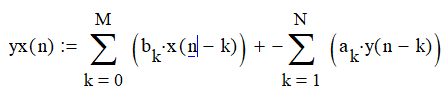

 Экспресс-анализ
АЧХ и ФЧХ:
Экспресс-анализ
АЧХ и ФЧХ:
Для оценки АЧХ звена второго порядка достаточно построить её график по пяти точкам: 1. двум – на границах основной полосы 0 и , 2. одной (уточняющей) – посередине основной полосы /2, 13 3. двум – внутри основной полосы, соответствующим максимуму и минимуму (либо нулю) АЧХ.

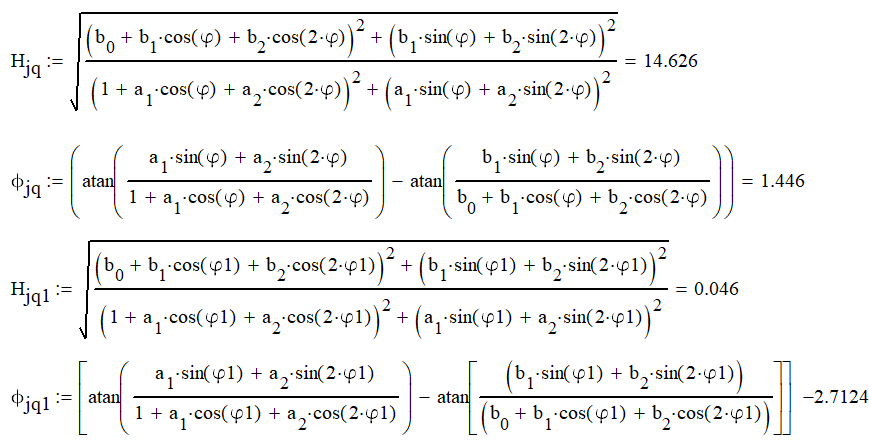

Эскизные кривые АЧХ и ФЧХ:
Оценка АЧХ
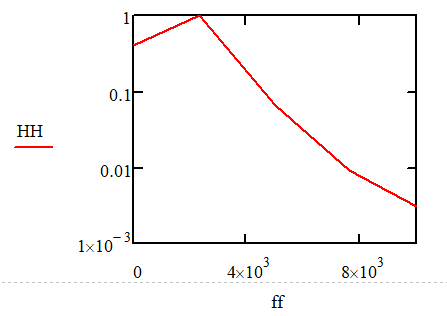
Оценка ФЧХ
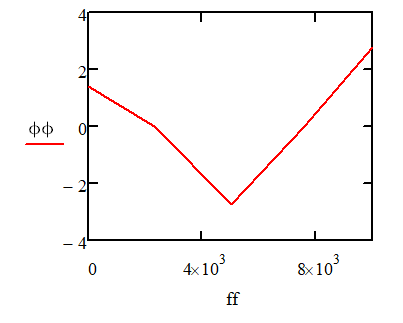
Выполнение лабораторной работы:
Рассчитанные и измеренные значения ИХ (H)
n |
Значения отсчетов ИХ h, рассчитанные по РУ |
Значения отсчетов ИХ h, рассчитанные по общей формуле |
Значения отсчетов ИХ h, измеренные экспериментально |
0 |
0.9 |
0.9 |
0.900000 |
1 |
-2.3544 |
-2.3544 |
-2.354420 |
2 |
3.0445 |
3.0445 |
3.044478 |
3 |
-2.1009 |
-2.1009 |
-2.100875 |
4 |
0.37069 |
0.37069 |
0.370695 |
5 |
1.123 |
1.123 |
1.122991 |
6 |
-1.7167 |
-1.7167 |
-1.716686 |
7 |
1.3401 |
1.3401 |
1.340108 |
8 |
-0.40771 |
-0.40771 |
-0.407709 |
9 |
-0.49751 |
-0.49751 |
-0.497512 |
Рассчитанные и измеренные значения реакции ЛДС на прямоугольный импульс (y)
n |
Значения отсчетов реакции y, рассчитанные по формуле свертки |
Значения отсчетов реакции y, рассчитанные по РУ |
Значения отсчетов реакции y, измеренные экспериментально |
0 |
0.9 |
0.9 |
0.900000 |
1 |
-1.4544 |
-1.4544 |
-1.454420 |
2 |
1.5901 |
1.5901 |
1.590058 |
3 |
-0.5108 |
-0.5108 |
-0.510817 |
4 |
-1.0401 |
-1.0401 |
-1.040122 |
5 |
2.4373 |
2.4373 |
2.437289 |
6 |
-2.3239 |
-2.3239 |
-2.323875 |
7 |
1.1171 |
1.1171 |
1.117108 |
8 |
0.3387 |
0.3387 |
0.338705 |
9 |
-1.2818 |
-1.2818 |
-1.281799 |
10 |
0.43488 |
1.3805 |
1.380467 |
11 |
-0.90521 |
-0.78979 |
-0.789793 |
12 |
-0.49751 |
-0.039956 |
-0.039957 |
Значения входного воздействия и реакции ЛДС, участвующие в разностном уравнении y со смещением на один вниз, полученные теоретически
n |
x(n) |
x(n-1) |
x(n-2) |
y(n) |
y(n-1) |
y(n-2) |
0 |
1 |
0 |
0 |
0.9 |
0 |
0 |
1 |
1 |
1 |
0 |
-1.4544 |
0.9 |
0 |
2 |
1 |
1 |
1 |
1.5901 |
-1.4544 |
0.9 |
3 |
1 |
1 |
1 |
-0.5108 |
1.5901 |
-1.4544 |
4 |
0 |
1 |
1 |
-1.0401 |
-0.5108 |
1.5901 |
5 |
0 |
0 |
1 |
2.4373 |
-1.0401 |
-0.5108 |
6 |
0 |
0 |
0 |
-2.3239 |
2.4373 |
-1.0401 |
7 |
0 |
0 |
0 |
1.1171 |
-2.3239 |
2.4373 |
8 |
0 |
0 |
0 |
0.3387 |
1.1171 |
-2.3239 |
9 |
0 |
0 |
0 |
-1.2818 |
0.3387 |
1.1171 |
10 |
0 |
0 |
0 |
1.3805 |
-1.2818 |
0.3387 |
11 |
0 |
0 |
0 |
-0.78979 |
1.3805 |
-1.2818 |
12 |
0 |
0 |
0 |
-0.039956 |
-0.78979 |
1.3805 |
Значения входного воздействия, реакции ЛДС и значения, хранящиеся в элементах памяти ЛДС, измеренные экспериментально
n |
x(n) |
x(n-1) |
x(n-2) |
y(n) |
y(n-1) |
y(n-2) |
0 |
1 |
0 |
0 |
0.900000 |
0 |
0 |
1 |
1 |
1 |
0 |
-1.454420 |
0.900000 |
0 |
2 |
1 |
1 |
1 |
1.590058 |
-1.454420 |
0.900000 |
3 |
1 |
1 |
1 |
-0.510817 |
1.590058 |
-1.454420 |
4 |
0 |
1 |
1 |
-1.040122 |
-0.510817 |
1.590058 |
5 |
0 |
0 |
1 |
2.437289 |
-1.040122 |
-0.510817 |
6 |
0 |
0 |
0 |
-2.323875 |
2.437289 |
-1.040122 |
7 |
0 |
0 |
0 |
1.117108 |
-2.323875 |
2.437289 |
8 |
0 |
0 |
0 |
0.338705 |
1.117108 |
-2.323875 |
9 |
0 |
0 |
0 |
-1.281799 |
0.338705 |
1.117108 |
10 |
0 |
0 |
0 |
1.380467 |
-1.281799 |
0.338705 |
11 |
0 |
0 |
0 |
-0.789793 |
1.380467 |
-1.281799 |
12 |
0 |
0 |
0 |
-0.039957 |
-0.789793 |
1.380467 |
Амплитудно-частотная
характеристика (АЧХ), представленная в
линейном масштабе.
Амплитудный спектр входного сигнала (прямоугольного импульса) в линейном масштабе.
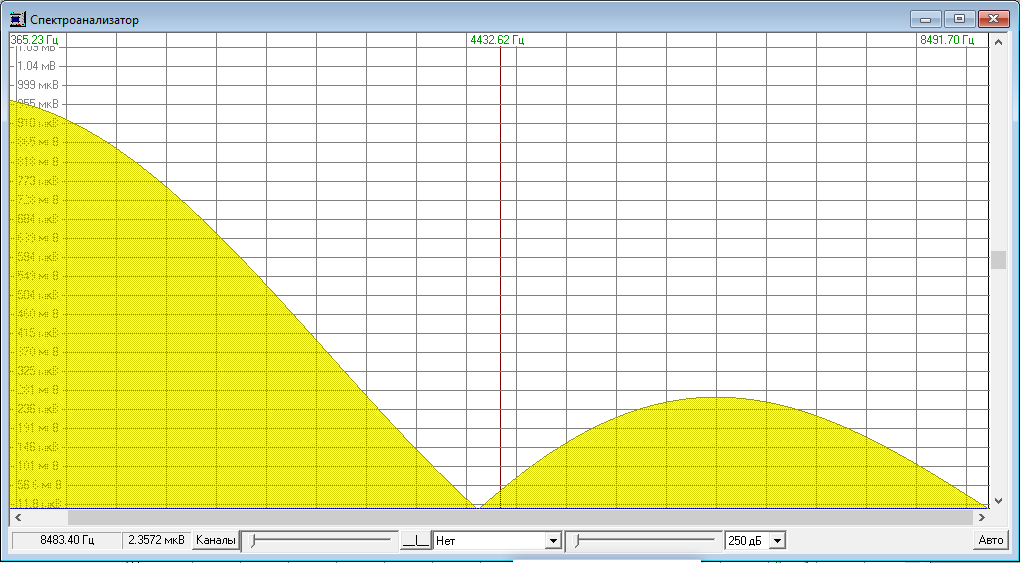
Амплитудный спектр выходного сигнала (прямоугольного импульса) в линейном масштабе.

Москва 2024
