МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

(МИНЦИФРЫ РОССИИ)

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПБГУТ)

Кафедра радиосистем и обработки сигналов (РОС)

Курсовой проект

по дисциплине «Помехоустойчивость радиоэлектронных средств»

Тема работы: Исследование кодеков помехоустойчивых кодов

Выполнил: студент 4 курса

Факультета: РТС

Направление: 11.03.01

Группа:

ФИО

________________

Зачётная книжка: №

Вариант: №5

Проверил: Глушанков Евгений Иванович

Оценка:______________

Подпись______________

Дата:______________

Санкт-Петербург

2023

Оглавление

Исходные данные для выполнения курсового проекта 3

1. Теоретическая часть 3

2. Исследование кода Хэмминга (15,11) 6

3. Исследование кода БЧХ (15,11) 8

4. Исследование свёрточного кода 10

Заключение 16

Исходные данные для выполнения курсового проекта

Таблица 1. Общие данные для курсового проекта

КХ	БЧХ	СК-1	СК-2
Б) (15,11)	А) (15,11)	11 16 13	РТ 0.2

1. Теоретическая часть

1.1 Области применения помехоустойчивого кодирования в радиотехнических системах.

Коды обнаружения ошибок (которые могут только установить факт ошибки) принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).

Коды, исправляющие ошибки, применяются в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам, а также в системах хранения информации, в том числе магнитных и оптических. Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.

1.2 Классификация ПУ кодов. Принцип ПУ кодирования.

Корректирующий код (также помехоустойчивый код) — код, предназначенный для обнаружения и исправления ошибок.

Основная техника — добавление при записи (передаче) в полезные данные специальным образом структурированной избыточной информации (например, контрольного числа), а при чтении (приёме) использование такой избыточной информации для обнаружения и исправления ошибки. Число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.

По способу работы с данными коды, исправляющие ошибки, делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.

1.3 Помехоустойчивые коды:

- Код Хэмминга:

Коды Хэмминга представляют собой семейство линейных кодов общего вида. Коды Хэмминга могут обнаруживать однобитные и двухбитные ошибки или исправлять однобитные ошибки без обнаружения неисправленных ошибок. Напротив, простой код четности не может исправлять ошибки и может обнаруживать только нечетное количество ошибочных бит. Коды Хэмминга являются совершенными кодами, то есть они достигают максимально возможной скорости для кодов с длиной блока и минимальным расстоянием, равным трем.

С математической точки зрения коды Хэмминга представляют собой класс двоичных линейных кодов. Для каждого целого числа r ≥ 2 существует кодовое слово с длиной блока n = 2^r - 1 и длиной сообщения k = 2^r - r - 1. Следовательно, скорость кодов Хэмминга равна R = k/n = 1 - r/(2^r - 1), что является максимально возможным для кодов с минимальным расстоянием, равным трем (т. е. минимальное количество изменений битов, необходимое для перехода от любого кодового слова к любому другому кодовому слову, равно трем) и длине блока 2^ r - 1. Матрица проверки четности кода Хэмминга строится путем перечисления всех столбцов длины r, которые не равны нулю. Матрица проверки четности обладает тем свойством, что любые два столбца попарно линейно независимы.

- Циклические коды, коды БЧХ:

Несмотря на то, что декодирование линейных кодов значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.

Циклическим кодом является линейный код, обладающий следующим свойством: если �→  является кодовым словом, то его циклическая перестановка также является кодовым словом.

Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово �→=(�0,�1,…,��−1) 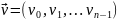 представляется в виде полинома �(�)=�0+�1�+…+��−1��−1 . При этом циклический сдвиг кодового слова эквивалентен умножению многочлена на �x по модулю ��−1xⁿ - 1.

Чаще всего используются двоичные циклические коды (то есть �0,�1,…  могут принимать значения 0 или 1).

Порождающим полиномом циклического (n,k) кода С называется такой ненулевой полином 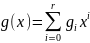из С степень которого наименьшая и коэффициент при старшей степени g_r = 1.

Коды Боуза — Чоудхури — Хоквингема (БЧХ-коды) — в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с заранее определёнными корректирующими свойствами, а именно, минимальным кодовым расстоянием. Частным случаем БЧХ-кодов является код Рида — Соломона.

БЧХ-код является циклическим кодом, который можно задать порождающим полиномом. Для его нахождения в случае БЧХ-кода необходимо заранее определить длину кода n (она не может быть произвольной) и требуемое минимальное расстояние . 

Пусть α примитивный элемент поля GF(q^m) (то есть  ), пусть β = α^s, — элемент поля GF(q^m) порядка  . Тогда нормированный полином g(x) минимальной степени над полем GF(q), корнями которого являются d − 1 подряд идущих степеней   элемента β для некоторого целого l₀ (в том числе 0 и 1), является порождающим полиномом БЧХ-кода над полем GF(q) с длиной n и минимальный расстоянием  .

Число проверочных символов r равно степени g(x), число информационных символов k = n − r, величина d называется конструктивным расстоянием БЧХ кода. Если n = qm − 1, то код называется примитивным, иначе непримитивным. Так же, как и для циклического кода, кодовый полином c(x) может быть получен из информационного полинома m(x), степени не больше k − 1, путем перемножения m(x) и g(x):

c(x) = m(x)g(x).

- Свёрточные коды:

Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных. Такие коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.

Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.

Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.

Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.

Свёрточный код — это корректирующий ошибки код, в котором

1. на каждом такте работы кодера �k символов входной полубесконечной последовательности преобразуются в �>�n > k символов выходной последовательности

2. в преобразовании также участвуют �m предыдущих символов

3. выполняется свойство линейности (если двум кодируемым последовательностям �x и �y соответствуют кодовые последовательности �X и �Y, то кодируемой последовательности ��+��ax + by соответствует ��+��aX + bY).

Свёрточный код является частным случаем древовидных и решетчатых кодов.