электротех лаба 33

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

Московский технический университет связи и информатики

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра " Теории электрических цепей "

ОТЧЕТ

Лабораторная работа № 33 Исследование активных интегрирующих и дифференцирующих цепей

Выполнил:

Студент группы такой-то Иванов И.И.

Проверил:

Ст. преподаватель Овсянникова Е.А.

Дата защиты ____________2024г.

Москва 2024 г.

Цель работы: с помощью машинного эксперимента получить форму напряжения на выходе активных интегрирующих и дифференцирующих цепей при различных формах напряжения на входе. Сравнить полученные характеристики с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.

Выполнение

u₁(t) = U_msin(2πft), - синусоидальное входное напряжение

где U_m=1В – амплитуда входного напряжения;

f = 2 кГц – частота входного напряжения;

t ϵ [0;1] мс – время.

u₁(t)- прямоугольное входное напряжение

VZERO=–1 – минимальное значение, В;

VONE=1 – максимальное значение, В;

Р1=0 – начало переднего фронта, с;

Р2=0 –начало плоской вершины импульса, с;

Р3=0.25e-3 – конец плоской вершины импульса, с;

Р4=0.25e-3 – момент достижения уровня VZERO, с;

P5=0.5e-3 – период следования импульсов, с.

u₁(t)- треугольное входное напряжение

VZERO=-1, VONE=1, P1=0, P2=0.25e-3, P3=0.25e-3, P4=0.5e-3, P5=0.5e-3.

Для интегрирующей цепи:

u₂(t)=K_{1 ,}

u₂(t) – выходное напряжение

K₁ – коэффициент пропорциональности

Для активной интегрирующей цепи:

U₂ = (-1/ (jwRC)) U₁

Для дифференцирующей цепи:

u₂(t)= K₂(du₁/dt),

где

u₂(t) – выходное напряжение;

K₂ – коэффициент пропорциональности

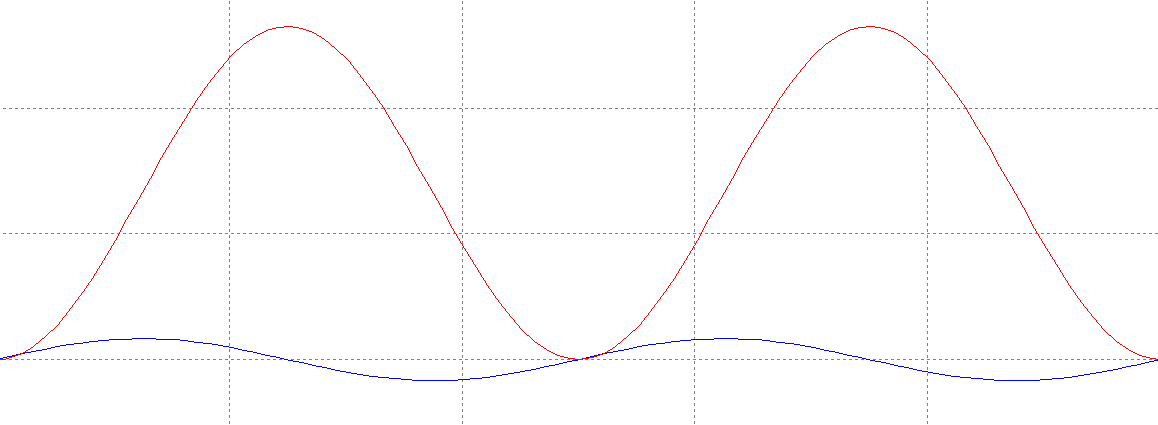
Рис. 1. График активной интегрирующей цепи при K = 10 и синусоидальном входном напряжении

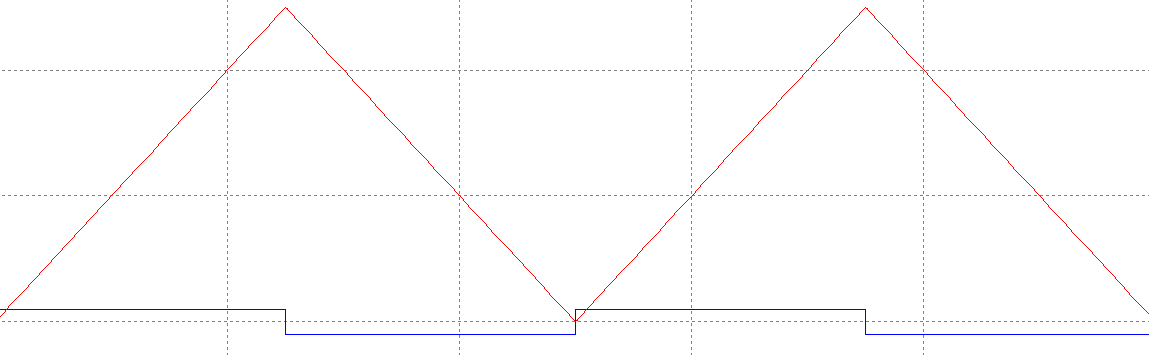
Рис. 2. График активной интегрирующей цепи при K = 10 и прямоугольном входном напряжении

Рис. 3. График активной интегрирующей цепи при K = 10 и треугольном входном напряжении

Для активной дифференцирующей цепи:

U₂=-jwRC U₁

Расчёт комплексно-передаточной функции интегрирующей цепи

C = 100 нФ, R = 1 кОм, f = 2 кГц

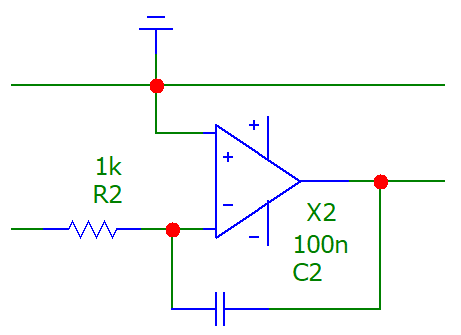
Рис. 4. схема интегрирующей цепи

H = U_вых/U_вх = (I*Z₂)/(I*(Z₁+Z₂)) = Z₂/(Z₁ + Z₂)

Z1 = R, Z2 = 1/iwC

H = (1/iwC)/(R+1/iwC) = (1/2iπfC)/(R+1/2iπfC)

H = 0,3877 – 0,4872i

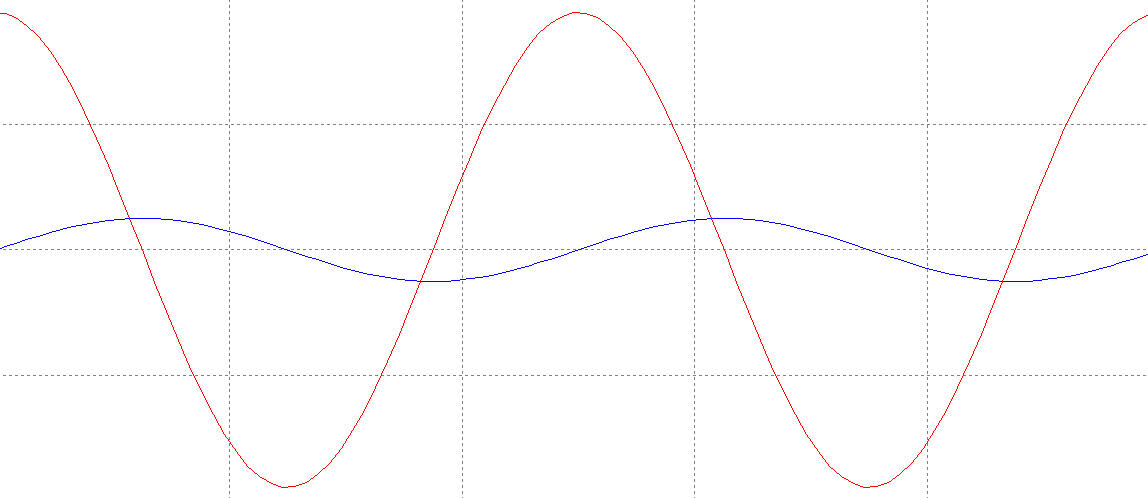
Рис. 5. График дифференцирующей цепи при K = 6 и синусоидальном входном напряжении

Рис. 6. График дифференцирующей цепи при K = 6 и прямоугольном входном напряжении

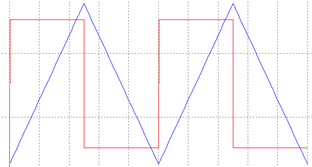
Рис. 7. График дифференцирующей цепи при K = 6 и треугольном входном напряжении

Расчёт комплексно-передаточной функции дифференцирующей цепи

C = 100 нФ, R = 1 кОм, f = 2 кГц

Рис. 8. схема дифференцирующей цепи

H = U_вых/U_вх = (I*Z₂)/(I*(Z₁+Z₂)) = Z₂/(Z₁ + Z₂)

Z1 = 1/iwC, Z2 = R

H = R/(R+1/iwC) = R/(R+1/2iπfC)

H = 0,6123 + 0,4872i

Рис. 9. схема активной интегрирующей цепи

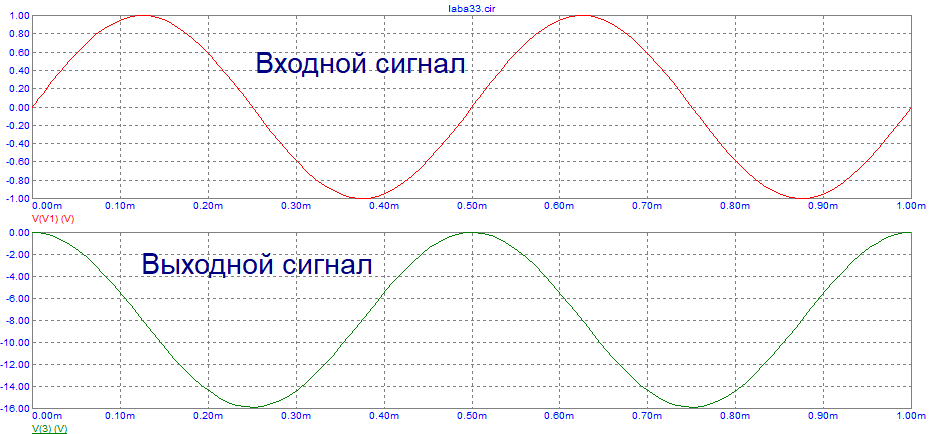
Рис. 10. Графики входного и выходного сигнала интегрирующей цепи синусоидального воздействия

Вывод: выходной сигнал интегрирующей активной цепи представляет собой проинтегрированный входной сигнал.

Рис. 11. Схема интегрирующей цепи при прямоугольном и треугольном воздействии

Рис. 12. Графики входного и выходного сигнала интегрирующей цепи при прямоугольном воздействии

Вывод: выходной сигнал интегрирующей активной цепи при прямоугольном воздействии представляет собой проинтегрированную прямоугольную последовательностью

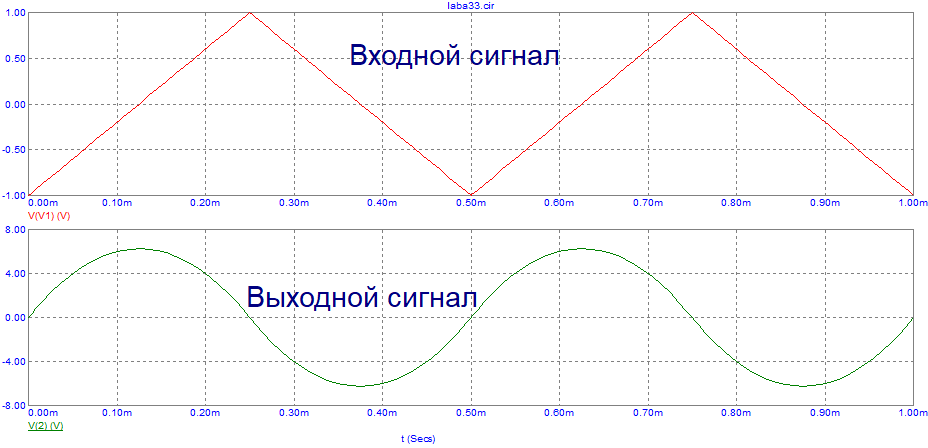
Рис. 13. Графики входного и выходного сигнала интегрирующей цепи при треугольном воздействии

Вывод: выходной сигнал интегрирующей активной цепи при треугольном воздействии представляет собой проинтегрированную пилообразную последовательностью

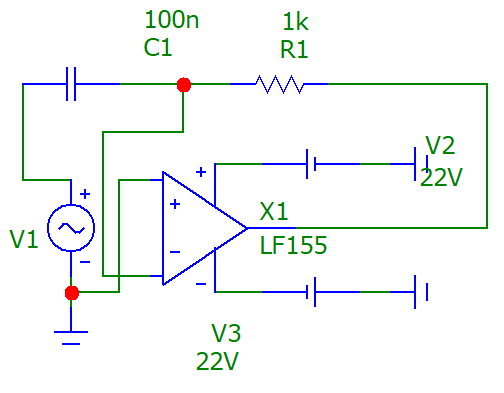
Рис. 14. Схема дифференцирующей цепи при синусоидальном воздействии

Рис. 15. Графики входного и выходного сигнала дифференцирующей цепи при синусоидальном воздействии

Вывод: выходной сигнал дифференцирующей активной цепи при синусоидальном воздействии представляет собой продифференцированную синусоиду.

Рис. 16. Схема дифференцирующей цепи при прямоугольном и треугольном воздействии

Рис. 17. Графики входного и выходного сигнала дифференцирующей цепи при прямоугольном воздействии

Вывод: выходной сигнал дифференцирующей активной цепи при прямоугольном воздействии представляет собой повторяющуюся последовательность продифференцированных прямоугольных импульсов.

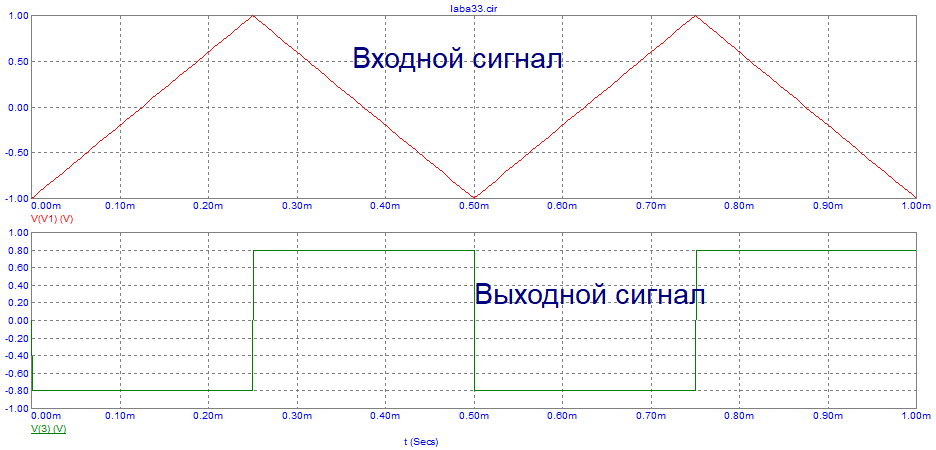Рис. 18. Графики входного и выходного сигнала дифференцирующей цепи при треугольном воздействии

Вывод: выходной сигнал дифференцирующей пассивной цепи при треугольном воздействии представляет собой повторяющуюся последовательность прямоугольных импульсов, которые являются производной от пилообразной последовательности

Вывод: с помощью машинного эксперимента получена форма напряжения на выходе активных интегрирующих и дифференцирующих цепей при различных формах напряжения на входе. Было проведено сравнение полученных характеристик с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.

Ответы на вопросы

1. Какие цепи являются интегрирующими? Приведите пример.

Ответ: интегрирующие цепи – это цепи, выходное напряжение которых пропорционально интегралу входного напряжения

Пример: пассивная RC-цепь

2. Какие цепи являются дифференцирующими? Приведите пример.

Ответ: дифференцирующие цепи – это цепи, выходное напряжение которых пропорционально производной входного напряжения по времени

Пример: пассивная CR-цепь

3. В каких случаях применяются интегрирующие цепи?

Ответ: для удлинения или расширения импульсов

4. В каких случаях применяются дифференцирующие цепи?

Ответ: для формирования импульсов малой длительности

5. Нарисуйте схему интегратора на ОУ и выведите его передаточную функцию H.

Рис. 19. Схема интегратора

H = U_вых/U_вх = (I*Z₂)/(I*(Z₁+Z₂)) = Z₂/(Z₁ + Z₂)

Z1 = R, Z2 = 1/iwC

H = (1/iwC)/(R+1/iwC) = (1/2iπfC)/(R+1/2iπfC)

6. Нарисуйте схему дифференциатора на ОУ и выведите его передаточную функцию H.

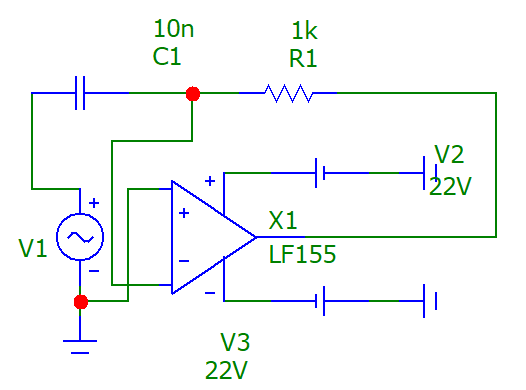
Рис. 20. Схема дифференциатора

H = U_вых/U_вх = (I*Z₂)/(I*(Z₁+Z₂)) = Z₂/(Z₁ + Z₂)

Z1 = 1/iwC, Z2 = R

H = R/(R+1/iwC) = R/(R+1/2iπfC)