электротех лаба 32

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

Московский технический университет связи и информатики

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра " Теории электрических цепей "

ОТЧЕТ

Лабораторная работа № 32 Исследование пассивных цепей при гармоническом воздействии на постоянной частоте

Выполнил:

Студент группы такой-то Иванов И.И.

Проверил:

Ст. преподаватель Овсянникова Е.А.

Дата защиты ____________2024г.

Москва 2024 г.

Цель работы: с помощью программы Micro-Cap исследовать электрический режим конденсатора и катушки индуктивности в цепях гармонического тока. Сравнить полученные характеристики с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.

Выполнение

C-цепь:

Z_C = -jX_C = = *e^-j90° = U_C / I = |U_C / I|*e^jarg(Uc/I) - комплексное сопротивление конденсатора

X_C = – емкостное сопротивление конденсатора

L-цепь:

Z_L = jX_L = jwL = wL*e^j90° = U_L / I = |U_L / I |* e^jarg(Uc/I) – комплексное сопротивление катушки

X_L = ωL – индуктивное сопротивление катушки

I = U / Z – комплексный ток

U = Z * I – комплексное падение напряжения

U_L = jwL * I = |U_L|*e^j90° - комплексное напряжение на катушке

U_C = * I = |U_C|*e^-j90° - комплексное напряжение на конденсатор

Выполнение

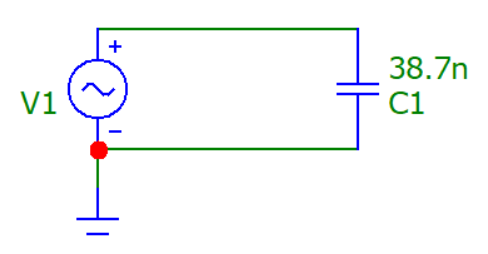
Рис. 1. Схема C-цепи

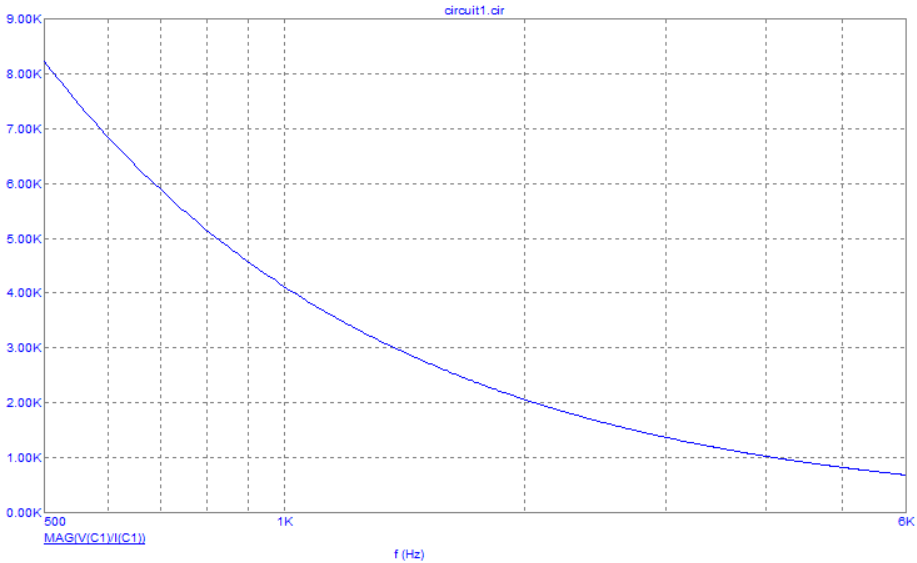
Рис. 2. График зависимости модуля сопротивления С-цепи от частоты

Вывод: при увеличении частоты модуль сопротивления уменьшается

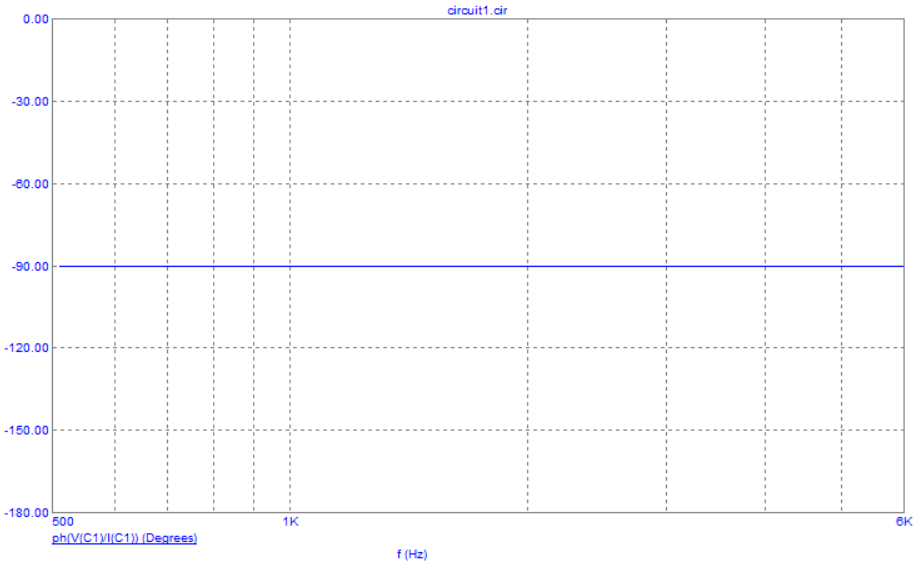
Рис. 3. График зависимости фазы сопротивления С-цепи от частоты

Вывод: при увеличении частоты фаза сопротивления не изменяется

Таблица 1 – расчёты для сопротивления

По предварительному расчету						Получено экспериментально
f, кГц	C, нФ	ZC, Ом	|ZC|, Ом	arg(ZC), град.	|ZC|, Ом		arg(ZC), град.
1	38,7	-4114,6 j	4114,6	-90	4113		-90
2	38,7	-2057,3 j	2057,3	-90	2056		-90
3	38,7	-1371,5 j	1371,5	-90	1371		-90
4	38,7	-1028,7 j	1028,7	-90	1028		-90
5	38, 7	-822,92 j	822,92	-90	822,5		-90

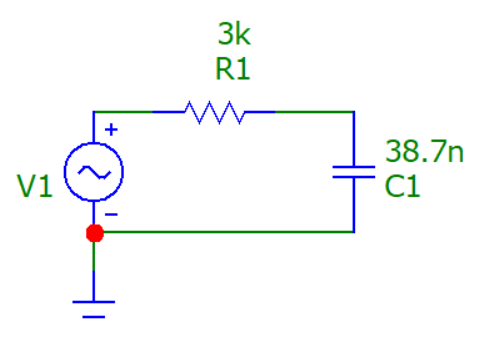
Рис. 4. Схема RC-цепи

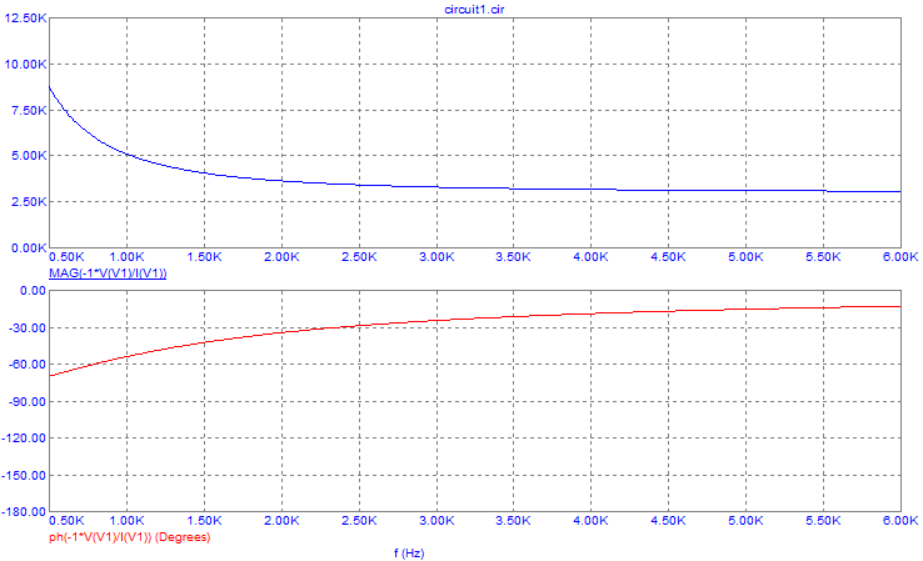
Рис. 5. Графики зависимости модуля и фазы комплексного сопротивления RС-цепи от частоты

Вывод: при увеличении частоты модуль комплексного сопротивления уменьшается, а фаза увеличивается

Таблица 2 – расчёты для комплексного сопротивления

По предварительному расчету						Получено экспериментально
f, кГц	C, нФ	R, кОм	ZRC, Ом	|ZRC|, Ом	arg|ZRC|, град.	|ZRC|, Ом	arg|ZRC|, град.
1	38,7	3	5092 e-53.9 j	5092 e-53.9	-53,9	5091	-53,89
2	38,7	3	3637,7 e-43.3 j	3637,7 e-29.4	-29,5	3637	-34,43
3	38,7	3	3298,64 e-24.6 j	3298,64 e-24.6	-24,6	3298	-24,56
4	38,7	3	3171,47 e-18.9 j	3171,47 e-18.9	-18,9	3171	-18,92
5	38,7	3	3110,8 e-15.3 j	3110,8 e-15.3	-15,3	3111	-15,33

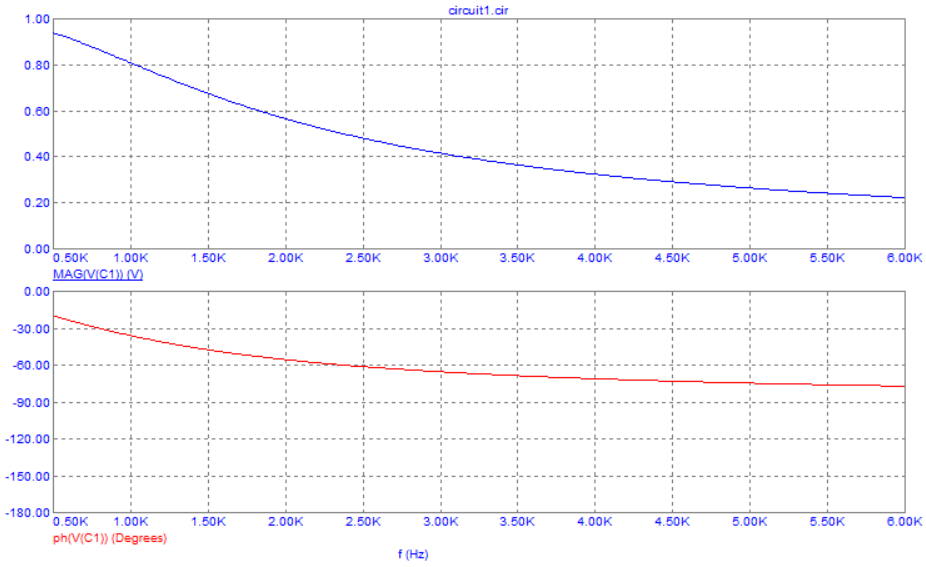
Рис. 6. Графики зависимости модуля и фазы комплексного напряжения на конденсаторе RС-цепи от частоты

Таблица 3 – расчёты для комплексного напряжения

По предварительному расчету							Получено экспериментально
f, кГц	C, нФ	R, кОм	U1, В	U2, В	φ, град.	U2, В		U2, В	φ, град.
1	38,7	3	0,707	0,571	-38,94	0,571 e-39 j		0,808	-36,11
2	38,7	3	0,707	0,4	-60,54	0,4 e-61 j		0,565	-55,57
3	38,7	3	0,707	0,294	-67,47	0,294 e-68 j		0,416	-65,44
4	38,7	3	0,707	0,229	-72,07	0,229 e-72 j		0,324	-71,08
5	38,7	3	0,707	0,264	-75,18	0,187 e-75 j		0,264	-74,67

Вывод: при увеличении частоты модуль и фаза напряжения на конденсаторе уменьшаются

Рис. 7. Схема L-цепи

Рис. 8. Графики зависимости модуля и фазы комплексного сопротивления катушки L-цепи от частоты

Таблица 4 – расчёты для комплексного сопротивления

По предварительному расчету					Получено экспериментально
f, кГц	L, мГн	ZL, Ом	|ZL|, Ом	arg(ZL), град.		|ZL|, Ом	arg(ZL), град.
1	31	194,68 j	194,68	90		194,78	90
2	31	389,36 j	389,36	90		389,56	90
3	31	584,04 j	584,04	90		584,34	90
4	31	780,58 j	780,58	90		779,12	90
5	31	973,4 j	973,4	90		973,89	90

Вывод: при увеличении частоты модуль комплексного сопротивления катушки увеличивается, а фаза не изменяется

Рис. 9. Схема RL-цепи

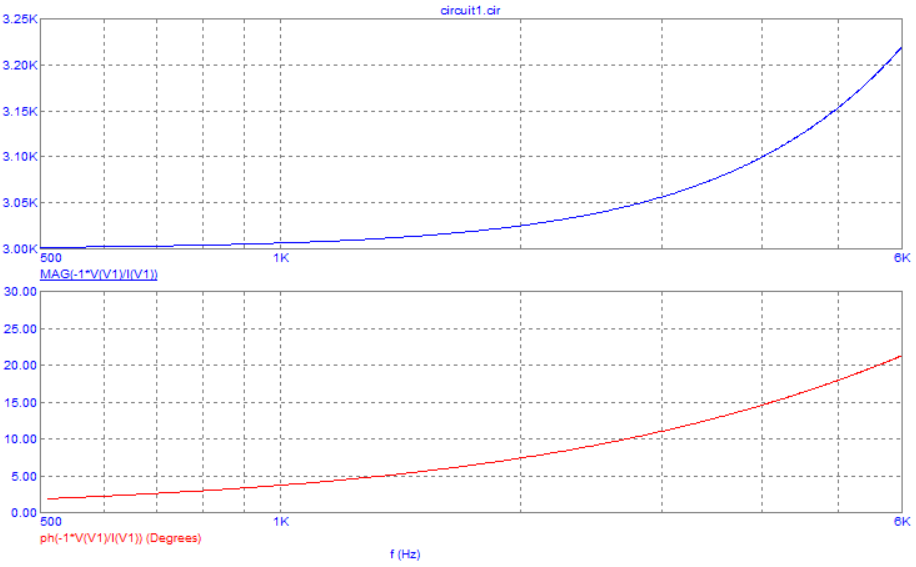
Рис. 10. Графики зависимости модуля и фазы комплексного сопротивления RL-цепи от частоты

Таблица 5 – расчёты для комплексного сопротивления

По предварительному расчету						Получено экспериментально
f, кГц	L, мГн	R, кОм	ZRL, Ом	|ZRL|, Ом	arg(ZRL), град.	|ZRL|, Ом	arg(ZRL), град.
1	31	3	3006,31 e4 j	3006,31 e4	3,7	3006	3,7
2	31	3	3025,16 e7 j	3025,16 e7	7,4	3025	7,4
3	31	3	3056,32 e11 j	3056,32 e11	11	3056	11
4	31	3	3099,89 e15 j	3099,89 e15	14,6	3100	14,6
5	31	3	3153,97 e18 j	3153,97 e18	18	3154	18

Вывод: при увеличении частоты модуль и фаза комплексного сопротивления увеличиваются

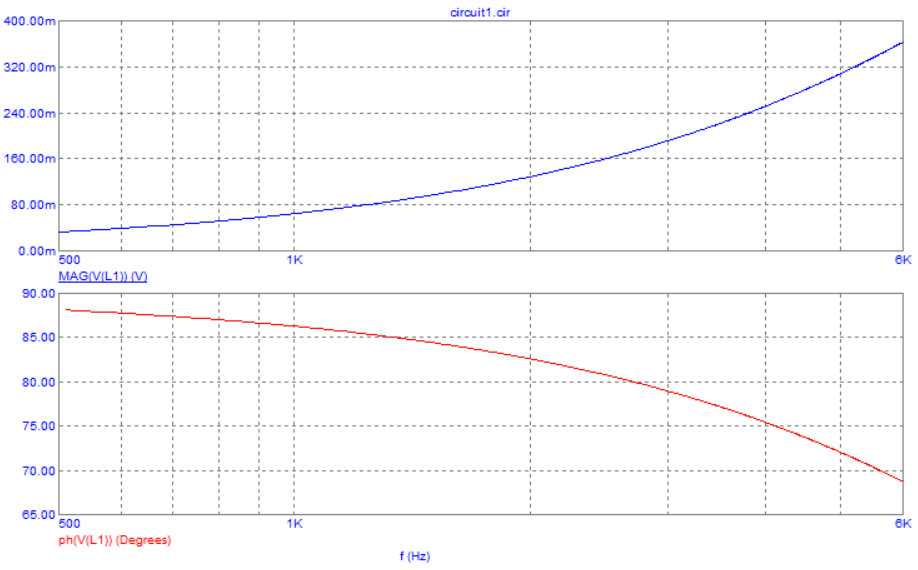
Рис. 11. Графики зависимости модуля и фазы комплексного напряжения на катушке RL-цепи от частоты

Таблица 6 – расчёты для напряжения

По предварительному расчету								Получено экспериментально
f, кГц	L, мГн	R, кОм	U1, В	U2, В	φ, град.	U2, В	U2, В		φ, град.
1	31	3	0,707	0,046	86,3	0,046 e4 j	0,064		86,29
2	31	3	0,707	0,091	82,7	0,091 e7 j	0,129		82,60
3	31	3	0,707	0,136	79,1	0,136 e11 j	0,191		78,98
4	31	3	0,707	0,178	75,9	0,178 e14 j	0,251		75,44
5	31	3	0,707	0,218	72,8	0,218 e17 j	0,308		72,02

Вывод: при увеличении частоты модуль комплексного напряжения увеличивается, а фаза уменьшается

Вывод: был исследован электрический режим конденсатора и катушки индуктивности в цепях гармонического тока в программе. Полученные характеристики полученные с помощью программы были сравнены с характеристиками, полученными расчетным путем

Ответы на вопросы

1. Какая частота называется граничной для RL-цепи?

Ответ: Граничная частота – частота, при которой резистивное сопротивление равно реактивному (R = wL)

F_гр = R/(2*pi*L) = 100/(2*3,14*0,045) = 353,67 Гц

2. Каково значение модуля входного сопротивления RL-цепи на граничной частоте?

Ответ: Z_вх = (R² + X²)^1/2 = (R² + (2*pi*f_гр*L)²)^1/2 = 141,41 Ом

3. Каково значение аргумента входного сопротивления RL-цепи на граничной частоте?

arg(Z) = arctg(wL/R) = 0,78 ~ 44,59^o

4. К чему стремиться модуль тока RL-цепи при увеличении частоты?

Ответ: I = U_вх/Z_вх = U_вх/(R² + (2*pi*f_гр*L)²)^1/2 -> при увеличении частоты модуль тока будет стремиться к 0

5. Чему равен модуль входного сопротивления RL-цепи при частоте равной нулю?

Z = (R² + (2*pi*f_гр*L)²)^1/2 = R = 100 Ом