электротех лаба 17

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

Московский технический университет связи и информатики

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра " Теории электрических цепей "

ОТЧЕТ

Лабораторная работа № 17 Исследование на ЭВМ резонансных явлений в пассивном

параллельном колебательном контуре

Выполнил:

Студент группы такой-то Иванов И.И.

Проверил:

Ст. преподаватель Овсянникова Е.А.

Дата защиты ____________2024г.

Москва 2024 г.

Цель работы: С помощью программы Micro-Cap получить входные и передаточные характеристики одиночного параллельного колебательного контура при различных добротностях.

Выполнение

Im(Y_вх) = 0

Y_вх = – комплексная входная проводимость контура

Im(Y_вх) =

– резонансная частота

– характеристическое сопротивление

– добротность

– нижняя граничная частота

– верхняя граничная частота

П = f₂ – f₁ – абсолютная полоса пропускания

– комплексное входное сопротивление

– модуль входного сопротивления при условии, что меняется только частоты источника напряжения

– фаза входного сопротивления в градусах

I = , , , – комплексные токи

– добротность последовательного контура

– сопротивление

– резонансная частота контура

– комплексное входное сопротивление

– модуль входного сопротивления при резонансе

R = 14 кОм, f_р = 5 кГц

-> L =

При C = 30 нФ, L = 0,033 Гн

По предварительному расчету R=14кОм, fр=5 кГц, C=30*10^-9 Ф, L=0,033 Гн							Получено экспериментально
p, Ом	Q	f1, кГц	f2, кГц	П, кГц	Z(fp), Ом	f0, кГц	fp, Гц	Z(fp), Ом	f1, кГц	f2, кГц	П, кГц	Q
1048	13,35	4,87	5,25	0,38	186000	5	5060	186000	4,88	5,25	0,38	13,35

Таблица 1 – расчёты для пассивного параллельного колебательного контура

Рис. 1. Схема пассивного параллельного колебательного контура

Рис. 2. График зависимости модуля входного сопротивления от частоты

Вывод: до резонансной частоты модуль входного сопротивления возрастает, а после уменьшается

Рис. 3. График зависимости фазы входного сопротивления от частоты

Вывод: фаза входного сопротивления постоянно уменьшается, но в области резонансной частоты идёт резкий спад

Рис. 4. График зависимостей модуля входного тока от частоты

Вывод: L постоянно уменьшается, C постоянно увеличивается, R неизменно, V до резонансной частоты уменьшается, а после увеличивается

По предварительному расчету C2=30*10^-9 Ф, L=0,033Гн				Получено экспериментально
Q	R, Ом	fp1, кГц	Z(fp), кОм	fp1, кГц	Z(fp), кОм
2	524,4	5	2,09	5	2,10
100	10,4	5	104	5	104

Таблица 2 – расчёты для контура первого типа

Рис. 5. Схема контура первого типа

Рис. 6. График зависимости модуля входного сопротивления от частоты при R = 524,4 Ом

Вывод: до резонансной частоты модуль входного сопротивления возрастает, а после уменьшается

Рис. 7. График зависимости фазы входного сопротивления от частоты при R = 524,4 Ом

Вывод: фаза входного сопротивления постоянно уменьшается, но в области резонансной частоты падение быстрее

Рис. 8. График зависимостей модуля входного тока от частоты при R = 524,4 Ом

Вывод: L постоянно уменьшается, C постоянно увеличивается, V до резонансной частоты уменьшается, а после увеличивается

Рис. 9. График зависимости модуля входного сопротивления от частоты при R = 10,4 Ом

Вывод: до резонансной частоты модуль входного сопротивления возрастает, а после уменьшается, причём в области резонансной частоты идёт резкий скачок

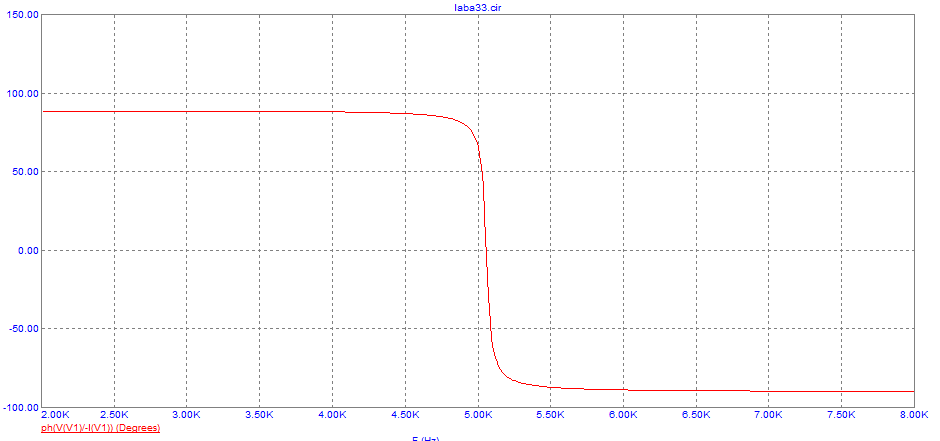
Рис. 10. График зависимости фазы входного сопротивления от частоты при R = 10,4 Ом

Вывод: фаза входного сопротивления постоянно уменьшается, но в области резонансной частоты падение быстрее

Рис. 11. График зависимостей модуля входного тока от частоты при R = 10,4 Ом

Вывод: L постоянно уменьшается, C постоянно увеличивается, V до резонансной частоты уменьшается, а после увеличивается, при этом совершая резкий переход

Вывод: С помощью программы Micro-Cap были получены входные и передаточные характеристики одиночного параллельного колебательного контура при различных добротностях.

Ответы на контрольные вопросы

1. Почему резонанс в параллельном пассивном колебательном контуре называется резонансом токов?

Ответ: Резонанс в параллельном колебательном контуре называется резонансом токов, потому что токи в цепях с индуктивностью и емкостью равны и находятся в противофазе. Поэтому ток в цепи имеет только активную составляющую.

2. Как рассчитывается резонансная частота параллельного колебательного контура?

Ответ:

3. Что такое добротность параллельного пассивного колебательного контура?

Ответ: Добротность – характеристика показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

4. Что такое полоса пропускания параллельного пассивного колебательного контура? Какие существуют способы расчета полосы пропускания?

Ответ: Полоса пропускания параллельного пассивного колебательного контура — это диапазон частот, который определяют по резонансной кривой на уровне 0,7 от максимального значения напряжения, соответствующей резонансной частоте.

Способы расчета: 1) Графический способ - способ, при котором полосу пропускания определяют непосредственно по графику.

2) Аналитический способ - способ, при котором рассчитывают нижнюю и верхнюю граничные частоты, а потом из верхней вычитают нижнюю.

5. Выведите уравнения, с помощью которых рассчитывают входные АЧХ и ФЧХ параллельного пассивного колебательного контура.

Ответ: Z_KK(jω)= = =

Так как вблизи от резонанса L , , получим окончательное выражение сопротивления паралленьго колебательного контура

= =

АЧХ: Z_ВХ(ω)=

ФЧХ: ϕ_Z(ω)=arg(z)