
электротех лаба 16
.docxМинистерство цифрового развития, связи и массовых коммуникаций Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
Московский технический университет связи и информатики
(МТУСИ)
Факультет "Радио и телевидение"
Кафедра " Теории электрических цепей "
ОТЧЕТ
Лабораторная работа № 16 Исследование на ЭВМ резонансных явлений в пассивном и
активном последовательном колебательном контуре
Выполнил:
Студент группы такой-то Иванов И.И.
Проверил:
Ст. преподаватель Овсянникова Е.А.
Дата защиты ____________2024г.
Москва 2024 г.
Цель работы: с помощью программы Micro-Cap исследовать характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.
Выполнение



И
так как
 ,
, получим
формулу:
,
, получим
формулу:
 – резонансная
частота контура
– резонансная
частота контура
 – характеристическое
сопротивление
– характеристическое
сопротивление
 – добротность
– добротность
 – нижняя
граничная частота
– нижняя
граничная частота
 – верхняя
граничная частота
– верхняя
граничная частота
П = f2 – f1 – абсолютная полоса пропускания
 – модуль
входного тока при резонансе
– модуль
входного тока при резонансе
 – резонансная
кривая тока при условии, что меняется
только частота источника напряжения
– резонансная
кривая тока при условии, что меняется
только частота источника напряжения
Предварительный расчёт
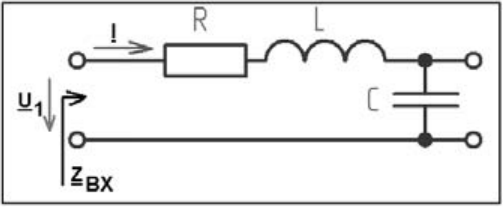
Рис. 1. Пассивный последовательный колебательный контур
C = [10; 40] нФ
f0 = 4,8 кГц
=>
L
=

При C = 21 нФ, L = 52 мГн
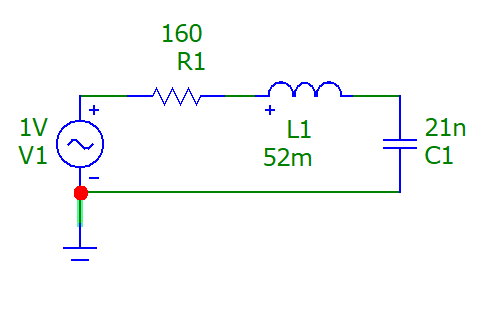
Рис. 2. Схема пассивного последовательного колебательного контура
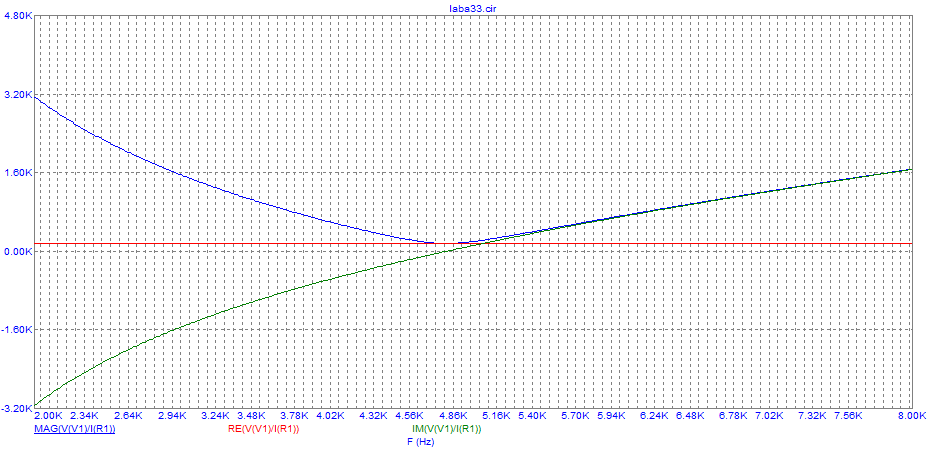
Рис. 3. График зависимости модуля(синий), действительной части(красный) и мнимой части(зелёный) входного сопротивления от частоты при R = 160 Ом
Вывод: модуль входного сопротивления до резонансной частоты уменьшается, а после увеличивается, действительная часть остаётся неизменной, а мнимая часть постоянно возрастает

Рис. 4. График зависимости модуля(синий), действительной части(красный) и мнимой части(зелёный) входного сопротивления от частоты при R = 640 Ом
Вывод: модуль входного сопротивления до резонансной частоты уменьшается, а после увеличивается, действительная часть остаётся неизменной, а мнимая часть постоянно возрастает

Рис. 5. График зависимости фазы входного сопротивления от частоты при R = 160 Ом и R = 640 Ом
Вывод: фаза входного сопротивления при R = 160 на низких частотах меньше, вблизи резонансной частоты имеет большую производную, а на больших частотах больше чем при R = 640

Рис. 6. График зависимости модуля входного тока от частоты при R = 160 Ом и R = 640 Ом
Вывод: модуль входного тока при R = 160 возрастает и уменьшается быстрее чем при R = 640

Рис. 6. График зависимости модуля входного тока от частоты при L = 52мГн и L = 104 мГн
Вывод: при L = 104 мГн резонансная частота уменьшилась и стала 3,39 кГц, и модуль входного тока возрастает быстрее чем при L = 52 мГн

Рис. 6. График зависимости модуля входного тока от частоты при C = 21 нФ и C = 42 нФ
Вывод: при C = 42 нФ резонансная частота уменьшилась и стала 3,39 кГц
f0
=
G/2π
G = 0,1 См, C2 = 1 мкФ, R = 0,1 Ом, f = 5кГц
С1 = 10,1 мкФ

Рис. 7. Схема активного колебательного контура с гиратором
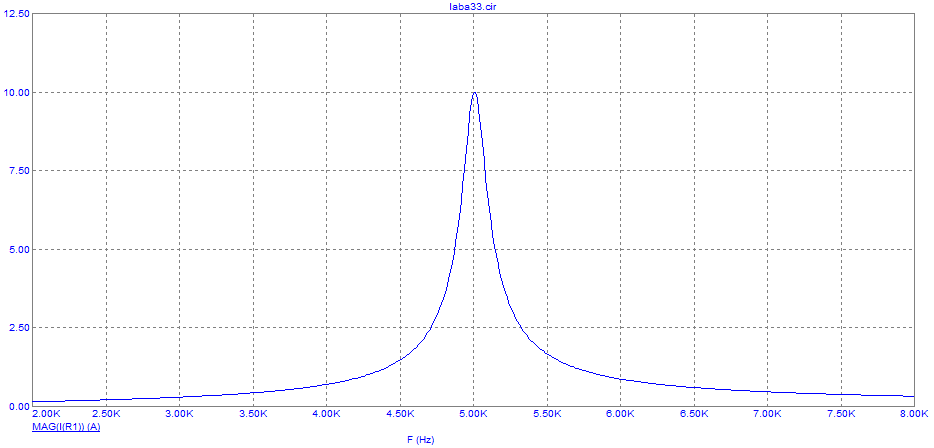
Рис. 8. График зависимости модуля входного тока от частоты при R = 0.1
Вывод: модуль входного тока до резонансной частоты увеличивается, а после уменьшается

Рис. 9. График зависимости модуля входного тока от частоты при R = 0.2
Вывод: модуль входного тока до резонансной частоты увеличивается, а после уменьшается, но делает это медленнее чем при R = 0.1
По предварительному расчёту U1 = 1В, f0 = 4,8 кГц, C = 21 нФ, L = 52 мГн |
Получено экспериментально |
||||||||||||
R, Ом |
p, Ом |
Q |
f1, кГц |
f2, кГц |
П, кГц |
I0, А |
f0, кГц |
f0, кГц |
I0, А |
f1, кГц |
f2, кГц |
П, кГц |
Q |
160 |
3315,7 |
4,55 |
4,68 |
4,91 |
0,23 |
0,006 |
4,8 |
4,8 |
0,006 |
4,68 |
4,91 |
0,23 |
20,7 |
640 |
3315,7 |
2,28 |
4,36 |
5,28 |
0,92 |
0,0015 |
4,8 |
4,8 |
0,0015 |
4,36 |
5,28 |
0,93 |
5,17 |
Гиратор |
|||||||||||||
По предварительному расчёту U1 = 1В, f0 = 5 кГц, C2 = 1мкФ, G = 0,1 См |
Поучено экспериментально |
||||||||||||
R, Ом |
C2, мкФ |
f0, кГЦ |
|||||||||||
0,1 |
10,14 |
5 |
|||||||||||
Вывод: с помощью программы Micro-Cap были исследованы характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.
Ответы на вопросы
1. Почему резонанс в последовательном пассивном колебательном контуре называется резонансом напряжений?
Ответ: Напряжение на индуктивном и ёмкостном элементах полностью компенсируют друг друга, а напряжение на резистивном элементе становится равным напряжению источника
2. Как рассчитывается резонансная частота сложного пассивного колебательного контура и как она рассчитывается для схем содержащих гиратор?
Ответ:
 (с
гиратором)
(с
гиратором)
3. Что такое добротность последовательного пассивного колебательного контура?
Ответ: Добротность последовательного колебательного контура – величина, показывающая во сколько раз сохраненной энергии в колебательном контуре больше, чем потери энергии за единичный период колебаний.
4. Что такое полоса пропускания последовательного пассивного колебательного контура? Какие существуют способы расчета полосы пропускания?
Ответ: Полоса пропускания — диапазон частот, в пределах которого амплитудно-частотная характеристика устройства достаточно равномерна для того, чтобы обеспечить передачу сигнала без существенного искажения его формы
– нижняя граничная частота;
– верхняя граничная частота;
П = f2 – f1 – абсолютная полоса пропускания.
5. Выведите уравнения, с помощью которых рассчитывают входные АЧХ и ФЧХ последовательного пассивного колебательного контура. Зависимость тока в контуре или напряжения на реактивных элементах от частоты питающего генератора при постоянном по величине напряжении генератора называется резонансной кривой или амплитудно-частотной характеристикой контура:

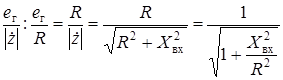 =
=
Реактивная составляющая входного сопротивления контура равна:

![]() -
относительная расстройка контура.
-
относительная расстройка контура.
При
небольших абсолютных расстройках
контура ![]() (в пределах полосы пропускания)
(в пределах полосы пропускания)
![]()
С учетом этого амплитудно-частотная характеристика контура
 ,
,
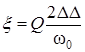 -
обобщенная расстройка контура
-
обобщенная расстройка контура
Окончательно уравнение амплитудно-частотной характеристики контура запишется в виде:

Фазовая характеристика контура
![]()
Из формулы для АЧХ контура найдем полосу пропускания:
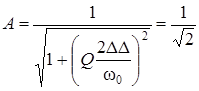
Отсюда
полоса пропускания контура на уровне
 Будет равна:
Будет равна:
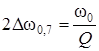 .
.
Зная резонансную частоту и полосу пропускания, можно рассчитать добротность контура:

Фазовая характеристика последовательного контура

