
ЛР3
.pdfФедеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»
им. В.И. Ульянова (Ленина)»
Кафедра биотехнических систем
ОТЧЕТ
по лабораторной работе №3
по дисциплине «Моделирование биологических процессов и систем»
ТЕМА: МОДЕЛИРОВАНИЕ СИГНАЛА ЭКГ
Вариант 1
Студентки гр. 0501 |
________________ |
Слободина Ю.А |
Преподаватель |
|
Тероева Ю. А. |
|
|
|
Санкт-Петербург
2023

ЛАБОРАТОРНАЯ РАБОТА № 3
МОДЕЛИРОВАНИЕ СИГНАЛА ЭКГ
Цель работы: изучить модели ЭКГ сигнала на основе генерации эта-
лона в виде суммы несимметричных гауссовых функций.
Задачи: написать код, построить графики.
Основные теоретические положения
В данной лабораторной работе предлагается реализовать базовую мо-
дель ЭКГ, приведенную в статье Т.Ю. Беклера «Моделирование искусствен-
ных электрокардиограмм нормальной и патологической формы».
В основу построения базовой математической модели генерации искус-
ственной ЭКГ положено аналитическое решение одного из дифференциаль-
ных уравнений. Базовая модель формируется по эталону ( ), который описы-
вается суммой несимметричных гауссовых функций:
При ограничениях:
где t0 – общая продолжительность (мс) z(t), а моменты начала t(1)i и окончания t(2)i каждого i-го фрагмента связаны с параметрами b(1)i и b(2)i , μi следующим образом:
Параметры Ai и μi определяют значения амплитуд и моментов времени,
когда i-ый информативный фрагмент эталона принимает максимальное значе-
ние при Ai > 0 или минимальное значение при Ai < 0, а параметры
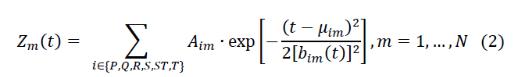
при 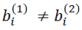 позволяют генерировать несимметричные фрагменты.
позволяют генерировать несимметричные фрагменты.
Известно, что в состоянии покоя сердечный ритм подвержен колеба-
ниям. Для моделирования этого явления на основе эталона последовательных временных интервалов формируется последовательность циклов по формуле
Изменение продолжительностей RR-интервалов моделируется искаже-
нием частоты сердечных сокращений на основе использования реализаций не-
зависимой случайной величины ym, которая с нулевым математическим ожи-
данием распределена на интервале [-y0,ym], y0 – фиксированное число, опре-
деляющее требуемые границы искажения частоты.

ПОЛНЫЙ КОД ПРОГРАММЫ
using Plots
struct WaveParams # структура для описания параметров волн name::String
A::Float64 b1::Float64 b2::Float64 mu::Float64
end
all_waves = Vector{WaveParams}() all_waves_depressST = Vector{WaveParams}()
push!(all_waves, WaveParams("P", 0.11, 0.014, 0.014, 0.399)) push!(all_waves, WaveParams("Q", -0.004, 0.008, 0.008, 0.45)) push!(all_waves, WaveParams("R", 1.453, 0.008, 0.008, 0.474)) push!(all_waves, WaveParams("S", -1.053, 0.007, 0.007, 0.495)) push!(all_waves, WaveParams("ST", 0.063, 0.04, 0.04, 0.574)) push!(all_waves, WaveParams("T", 0.52, 0.056, 0.024, 0.7))
push!(all_waves_depressST, WaveParams("P", 0.04, 0.003, 0.003, 0.203)) push!(all_waves_depressST, WaveParams("Q", 0, 0.066, 0.066, 0.266)) push!(all_waves_depressST, WaveParams("R", 0.64, 0.016, 0.026, 0.296)) push!(all_waves_depressST, WaveParams("S", -0.1, 0.03, 0.03, 0.4)) push!(all_waves_depressST, WaveParams("ST", -0.23, 0.15, 0.2, 0.45)) push!(all_waves_depressST, WaveParams("T", 0.06, 0.1, 0.08, 0.7))
#функция осуществляет моделирование комплекса по параметрам
#отдельных волн и с варьирующим значением ЧСС
function model_cmpx(all_waves::Vector{WaveParams},tOm::Float64, Fs::Number)
time_grid = collect(0:1/Fs:tOm) # временная сетка out = fill(0.0, length(time_grid))
for point in all_waves
# числитель формулы для Z(t) num = (time_grid.-point.mu).^2
# знаменатель считается в зависимости от mu
#так задается ассиметричность волны den = Float64[]
for t in time_grid if t < point.mu
push!(den, point.b1^2) else
push!(den, point.b2^2)
end
end
#в соотвествии с формулой результаты суммируем out.+= point.A*exp.(-num./den)
end

return out end
# в функцию добавлена вариативность амплитуды
function model_cmpx_var_ampl(all_waves::Vector{WaveParams},tOm::Float64, Fs::Number)
time_grid = collect(0:1/Fs:tOm) out = fill(0.0, length(time_grid))
V = -0.04:0.005:0.04 # вариативность амплитуды for point in all_waves
num = (time_grid.-point.mu).^2 den = Float64[]
for t in time_grid if t < point.mu
push!(den, point.b1^2) else
push!(den, point.b2^2)
end
end
# добавлена вариативность амплитуды out.+= (point.A+rand(V))*exp.(-num./den)
end return out end
ecg = Float64[] # пустой вектор, куда будет собран синт. сигнал ЭКГ ecg_depressST = Float64[]
ecg_ampl = Float64[]
Fs = 500
T = 1/Fs
t0_sec = 1 # базовая длина комплекса, в сек
#Rate = 100 #t0_sec = 60/Rate
V = -0.2:0.01:0.2 # допуски на вариабельность ритма
N = 20 # число комплексов
for m = 1:N # формируем синтетические сигналы t0m = t0_sec*(1+rand(V))
out = model_cmpx(all_waves, t0m, Fs) append!(ecg, out) # синтетическая ЭКГ
out = model_cmpx(all_waves_depressST, t0m, Fs) append!(ecg_depressST, out) # синт. ЭКГ с депрессией ST out = model_cmpx_var_ampl(all_waves, t0m, Fs)
append!(ecg_ampl, out) # синтетическая ЭКГ с вариативными амплитудами зубцов
end
plotly() # включаем возможность масштабирования
t = 0:T:T*length(ecg)-T # время для построения графика синтетической экг

dreyf = sin.(2*3.14*0.05*t) # дрейф изолинии (низкочастотная помеха) fifty_Hz = 0.3*sin.(2*3.14*50*t) # сетевая наводка
t_depressST = 0:T:T*length(ecg_depressST)-T # время для построения графика ЭКГ с депрессией сегмента ST
t_ampl = 0:T:T*length(ecg_ampl)-T # время для построения графика ЭКГ с варьирующей амплитудой
# графики
p1 = plot(t, ecg)
p2 = plot(t_depressST, ecg_depressST)
p3 = plot(t_ampl, ecg_ampl)
p4 = plot(t, ecg.+dreyf.+fifty_Hz) # к синтетической ЭКГ прибавляем дрейф и 50Гц
# настройки графиков, чтобы было красиво
#plot(p1, title = "Синтетическая ЭКГ, частота = $Rate в мин", xlabel = "Время, сек", ylabel = "Амплитуда, мв", legend = false, xticks = 0:0.2:20, yticks = - 1.2:0.1:1.4)
#plot(p1, title = "Синтетическая ЭКГ, частота = $Rate в мин", xlabel = "Время, сек", ylabel = "Амплитуда, мв", legend = false)
#plot(p1, title = "Синтетическая ЭКГ", xlabel = "Время, сек", ylabel = "Амплитуда, мв", legend = false, xticks = 0:0.2:20, yticks = -1.2:0.1:1.4) #plot(p1, title = "Синтетическая ЭКГ", xlabel = "Время, сек", ylabel = "Амплитуда, мв", legend = false)
#plot(p2, title = "ЭКГ c депрессией ST", xlabel = "Время, сек", ylabel = "Амплитуда, мв", legend = false, xticks = 0:0.2:20,yticks = -1.2:0.1:1.4) #plot(p2, title = "ЭКГ c депрессией ST", xlabel = "Время, сек", ylabel = "Амплитуда, мв", legend = false)
#plot(p3, title = "ЭКГ c варьирующей амплитудой зубцов", xlabel = "Время, сек", ylabel = "Амплитуда, мв", legend = false, xticks = 0:0.2:20, yticks = - 1.2:0.1:1.6)
#plot(p3, title = "ЭКГ c варьирующей амплитудой зубцов", xlabel = "Время, сек", ylabel = "Амплитуда, мв", legend = false)
#plot(p4, title = "ЭКГ c дрейфом изолинии и наводкой 50 Гц", xlabel = "Время,
сек", ylabel = "Амплитуда, мв", legend = false, xticks = 0:0.2:20, yticks = - 2:0.1:2)
#plot(p4, title = "ЭКГ c дрейфом изолинии и наводкой 50 Гц", xlabel = "Время,
сек", ylabel = "Амплитуда, мв", legend = false)
#plot(p1, p2, p3, p4, legend = false)
РЕЗУЛЬТАТ ВЫПОЛНЕНИЯ КОДА
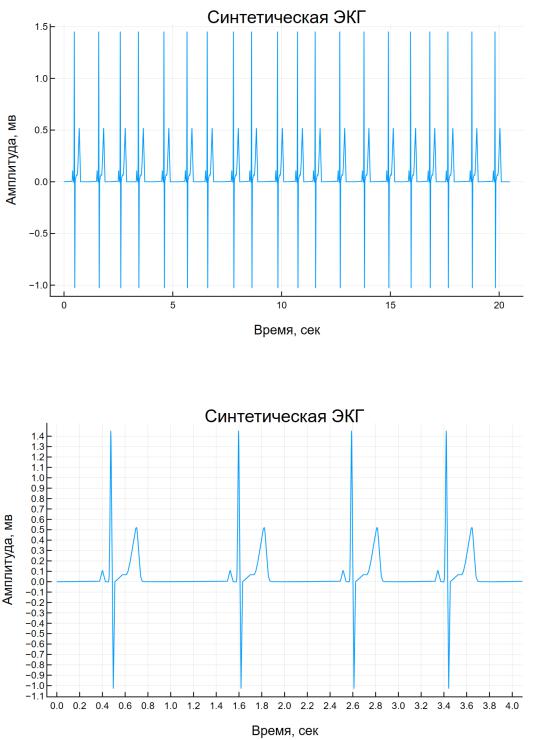
На рисунке 1 представлена синтетическая ЭКГ (все комплексы), на ри-
сунке 2 – 4 комплекса в увеличенном масштабе.
Рисунок 1 – Синтетическая ЭКГ (все 20 комплексов)
Рисунок 2 – Синтетическая ЭКГ в увеличенном масштабе
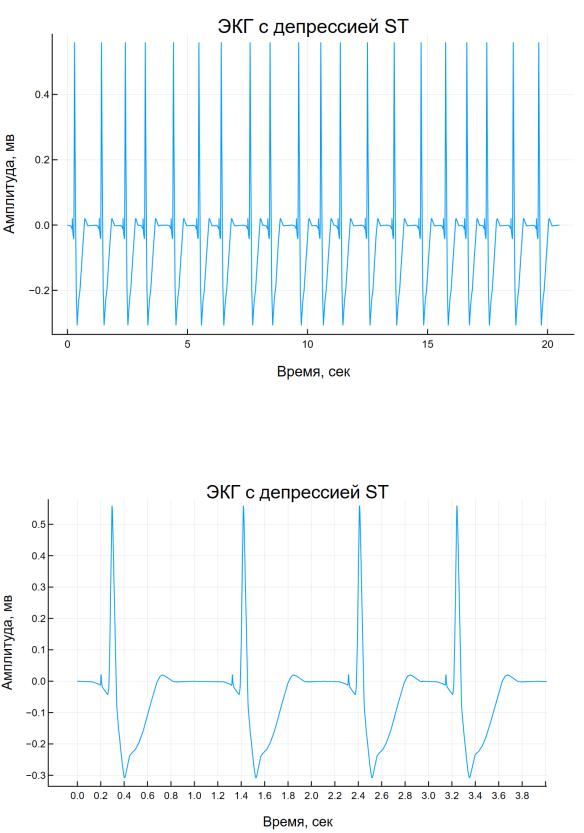
На рисунке 3 представлен синтетический сигнал ЭКГ с депрессией ST
(все комплексы), на рисунке 4 – в увеличенном масштабе.
Рисунок 3 – Синтетический сигнал ЭКГ с депрессией ST
(все 20 комплексов)
Рисунок 4 – Синтетический сигнал ЭКГ с депрессией ST
в увеличенном масштабе
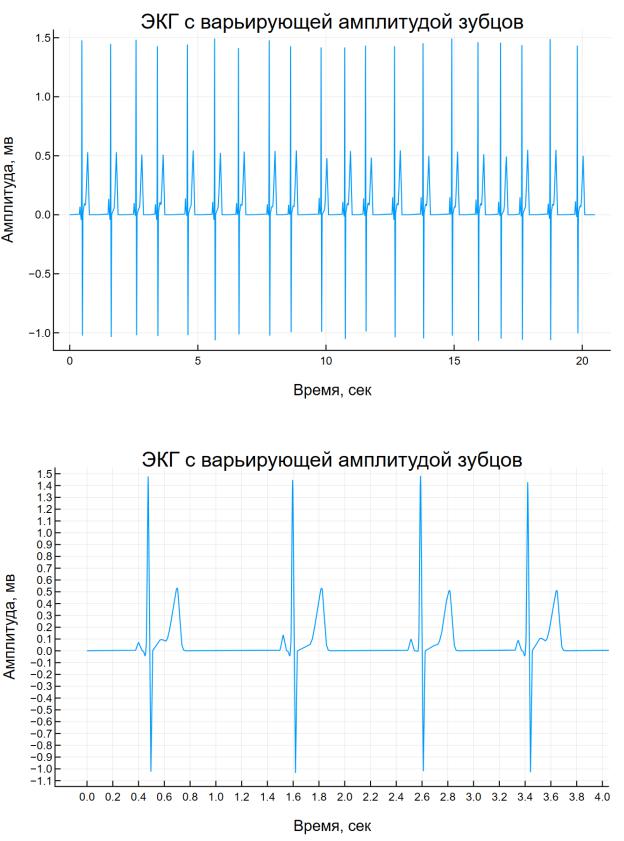
На рисунке 5 представлен сигнал ЭКГ с варьирующей амплитудой зуб-
цов, на рисунке 6 – в увеличенном масштабе.
Рисунок 5 – Сигнал ЭКГ с варьирующей амплитудой зубцов
Рисунок 6 – Сигнал ЭКГ с варьирующей амплитудой зубцов в увеличенном масштабе
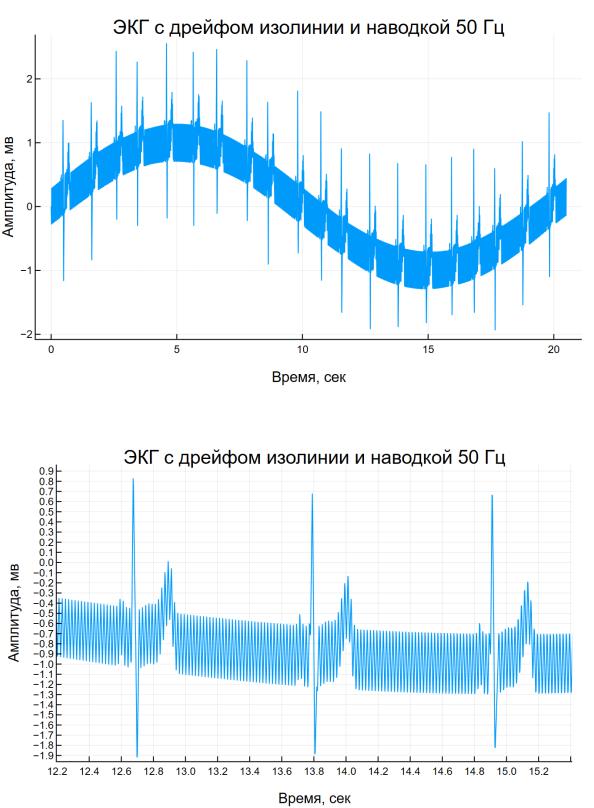
К синтетической ЭКГ добавлен дрейф изолинии и наводка в 50 Гц (рис. 7 и 8).
Рисунок 7 – Сигнал ЭКГ с дрейфом изолинии и наводкой 50 Гц
Рисунок 8 – Сигнал ЭКГ с дрейфом изолинии и наводкой 50 Гц в увеличенном масштабе
