
лр1
.pdfМИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра биотехнических систем
ОТЧЕТ по лабораторной работе №1
по дисциплине «Планирование медико-биологического эксперимента» Тема: Работа в R: данные и графики
Вариант 20
Студентка гр. 0501 |
|
Слободина Ю.А. |
|
Преподаватель |
|
|
Шевченко Д.С. |
Санкт-Петербург
2023
Теоретические данные:
Исходные данные представляют собой результат описания множества реализаций ЭКГ набором признаков ApEn (1), ApEn (2), ApEn (3), ApEn (4),
ApEn (5), ME.
Эти признаки получены в процессе вычисления и анализа параметров энтропии Колмогорова, которая отражает степень сложности (хаотичности)
ритмограммы.
Выборка данных включает несколько классов ЭКГ:
МА – мерцательная аритмия,
ЧЭ – частая экстрасистолия.
Каждый из классов представлен 25 объектами.
Задание:
Требуется сравнить значения признака ApEn (1) для двух групп сигналов ЭКГ (на выбор, например, НР и ЧЭ), используя для расчётов и визуализации результатов пакет R.
Исходные данные для варианта 20 представлены в таблице 1.
2
Экспериментальные результаты
Таблица 1 – Исходные данные
№ |
ApEn(1) |
ApEn(2) |
1 |
0.913 |
0.650 |
2 |
0.162 |
0.127 |
3 |
0.209 |
0.150 |
4 |
0.427 |
0.317 |
5 |
0.522 |
0.354 |
6 |
0.222 |
0.163 |
7 |
0.208 |
0.140 |
8 |
0.225 |
0.150 |
9 |
0.618 |
0.249 |
10 |
0.649 |
0.466 |
11 |
0.500 |
0.342 |
12 |
0.917 |
0.585 |
13 |
0.812 |
0.612 |
14 |
0.715 |
0.511 |
15 |
0.661 |
0.476 |
16 |
0.516 |
0.346 |
17 |
0.917 |
0.585 |
18 |
0.812 |
0.612 |
19 |
0.715 |
0.511 |
20 |
0.657 |
0.348 |
21 |
0.709 |
0.477 |
22 |
0.741 |
0.428 |
23 |
0.665 |
0.434 |
24 |
0.926 |
0.565 |
25 |
0.784 |
0.527 |
3

Код программы:
Создание двух переменных, соответствующих каждой выборке (столбцам)
x=read.table("name.txt")
x1=x[,1]
x2=x[,2]
Расчет среднего значения, выборочной дисперсии, СКО для двух выборок
>m1=mean(x1) # среднее значение первой выборки
>m1
[1] 0.60808
>m2=mean(x2) # среднее значение второй выборки
>m2
[1] 0.405
>d1=var(x1) # дисперсия первой выборки
>d1
[1] 0.05976808
>d2=var(x2) # дисперсия второй выборки
>d2
[1] 0.02792908
>sko1=sd(x1) # СКО первой выборки
>sko1
[1] 0.2444751
>sko2=sd(x2) # СКО второй выборки
>sko2
[1] 0.16712
Расчет значений верхнего и нижнего пределов доверительного интервала среднего значения для каждой переменной как , с доверительной вероятностью P=95%
4

- доверительный интервал среднего значения, где
уровень значимости равен
>n=length(x1) # объем выборки
>n
[1] 25
>df=n-1 # число степеней свободы
>df
[1] 24
>P=0.95 # доверительная вероятность
>alfa=1-P
>alfa [1] 0.05
>t=qt((1-alfa/2),df) # нахождение коэффициента Стьюдента
>t
[1] 2.063899
>deltax1=t*sko1/(sqrt(n)) # расчет доверительного интервала для выборки 1
>deltax1
[1] 0.1009144
>lp1=m1-deltax1 # нижний предел доверительного интервала для выборки 1
>lp1
[1] 0.5071656
>hp1=m1+deltax1 # верхний предел доверительного интервала для выборки 1
>hp1
[1] 0.7089944
>deltax2=t*sko2/(sqrt(n)) # расчет доверительного интервала для выборки 2
>deltax2
[1] 0.06898373
>lp2=m2-deltax2 # нижний предел доверительного интервала для выборки 2
>lp2
[1] 0.3360163
5
>hp2=m2+deltax2 # верхний предел доверительного интервала для выборки 2
>hp2
[1] 0.4739837
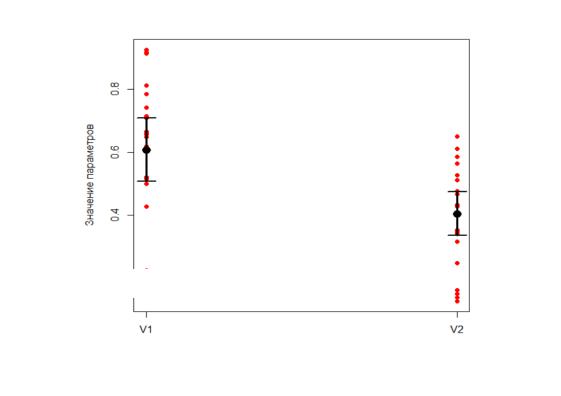
>stripchart(x,vertical=TRUE, xlab="Группа", ylab="Значение параметров", col="red", pch=16)
>points(c(1,2),c(m1,m2),,lwd=7)
>lines(c(1,1),c(lp1,hp1),lwd=3)
>lines(c(2,2),c(lp2,hp2),lwd=3)
>lines(c(0.97,1.03),c(lp1,lp1),lwd=2)
>lines(c(0.97,1.03),c(hp1,hp1),lwd=2)
>lines(c(1.97,2.03),c(lp2,lp2),lwd=2)
>lines(c(1.97,2.03),c(hp2,hp2),lwd=2)
Рисунок 1 - График значений параметров двух выборок, средних
значений и доверительных интервалов для двух переменных
6
Вывод:
В результате проделанной работы были проанализированы две выборки данных, для каждой из которых вычислены среднее значение,
выборочная дисперсия, выборочное СКО и доверительные интервалы среднего значения. Для наглядности полученных результатов был построен график значений параметров двух выборок, график средних значений и доверительных интервалов.
7
