
дзерж Теория графов методичка
.pdf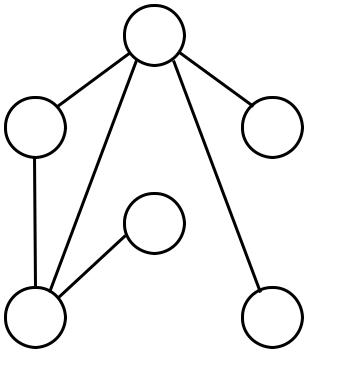
|
|
|
с |
(1,2,3,4) |
|
||
|
|
|
|
|
|
||
|
|
и |
|
|
а |
||
|
|
(2) |
|
|
|
||
|
|
|
|
|
(4) |
||
|
|
|
|
|
|
|
|
|
|
|
ы |
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
о |
|||
|
|
|
|
||||
|
|
(1,2,3) |
|
(1,4) |
|||
|
|
|
|
|
|||
|
|
|
Рисунок 5 |
||||
Геометрическая интерпретация гиперграфа, определяющая множество |
|||||||
сечений 2 |
3 = {{с, о, р}, {р; и; с}, {с; ы; р}, {о; с; а}} изображена на рисунке. В за- |
||||||
писи 2 |
3 индекс «3» показывает «местность» соотношения – сколь местно со- |
||||||
отношение. Однозначно задать s-отношение с помощью графа можно если в качестве носителя графа взять не только множество букв, но и множество идентификаторов слов. Такое задание s-отношения осуществляется посредством двухдольного графа.
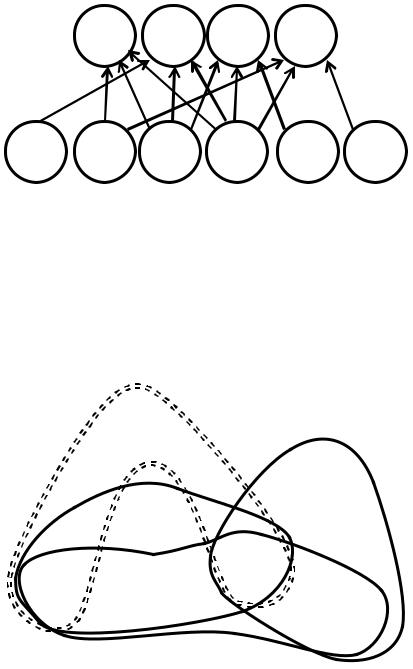
Граф = , называется двудольным графом или графом Кёнига, если его носитель разбит на 2 подмножества + и −, таких что: + ∩ − = { } – то есть не имеющих общих вершин. Начало каждой дуги принадлежит + и только ему, а конец - − и только ему. При заданном s-отношении элементам+ в графе Кёнига взаимно-однозначно сопоставляются буквы, а элементам − - идентификаторы слов.
Двудольный граф, заданный трёхместным соотношением 2
и идентификаторы ̅̅̅̅ изображен на рисунке.
2 (1,4)
11
1 |
2 |
3 |
4 |
и о р с ы а
Рисунок 6
Неплохо отметить для задания s-отношений применяется объект, прозванный в западной литературе «гиперграф». При геометрической интерпретации графа его буквы соответствуют вершинам, а слова – кругам Эйлера, которые охватывают буквы, входящие в состав слов
Рисунок 7
Одним из основных понятий в теории графов является понятие модели. Моделью Ψ называется совокупность множества с заданным на соотноше-
нии набором сечений: = { 11, 12, … , 1 , 21, 22, … 2 , 1, 2, … , },
где соответственно:-носитель модели,
соотношения ′ образуют сигнатуру модели.
Ψ = , . |
(2.13) |
12 |
|

§3. СВОЙСТВА БИНАРНЫХ ОТНОШЕНИЙ
Рассмотрим, какими вообще бывают бинарные (n=2) отношения:
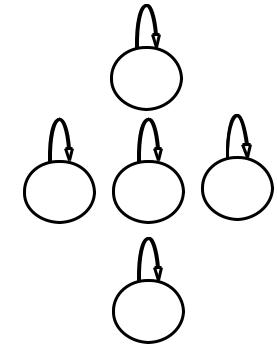
1.Если: ( ) (( ; ) 2) , то 2 называется рефлексивным. Рассматривая граф такого отношения можно сказать, что у каждой вершины такого графа есть петля. Матрица смежности – единичная.
2.Если: ( ; ( ≠ ) ) (( ; ) 2 ( ; ) 2), то 2
называется симметричным. Матрица смежности такого отношения будет симметрична относительно главной диагонали. При задании графом для каждых двух вершин есть две дуги, инцидентных и коинцидентных между собой.
3.Если: ( ; ; , ( ; ; )) (( ; ) 2&( ; )
2 ( ; ) 2), то 2 называется транзитивным. (здесь
( ; ; ) означает «попарно различны»). Для транзитивных отношений графы будут иметь такие характерные дуги:
Рисунок 8
Любой паре дуг, где конец одной совпадает с началом другой, соответствует третья дуга, транзитивно замыкающая этот порядок.
Таким образом, мы подходим к метрическим пространствам. Введём: Δ(2; ) – параметр близости бинарного отношения 2 к свойству – будет он оцениваться минимальным числом дуг, которые надо удалить или добавить
графу, задающему это отношение, чтобы полученный граф с отношением ̃
2
имел все 3 вышеприведенных свойства: = & &. (рефлексивность, симметричность, транзитивность).
13
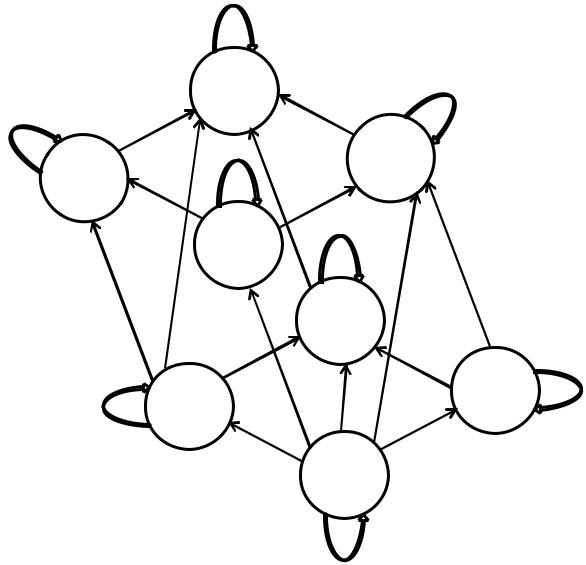
Определим близость для информационного графа машины Фон-Неймана, рассматриваемого ранее:
( 2, ) = 5 – рефлексивность ( ), ( 2, ) = 4 – симметричность ( ), ( 2, ) = 6 – транзитивность ( ).
Перечислим дуги, транзитивно ( ) замыкающие граф Фон-Неймана:
( , ) &( , ) , но ( , ) ( , ) &( , ) , но ( , ) ( , ) &( , ) , но ( , ) ( , ) &( , ) , но ( , ) ( , ) &( , ) , но ( , ) ( , ) &( , ) , но ( , )
Рефлективность ( ) для данного графа добавляется соответсвенно:
a
b c d
e
Рисунок 9
И, наконец, симметричность ( ) – дополняется следующим образом:
14

 a
a  b c d e
b c d e 
Рисунок 10
Продолжим список отношений:
4. Отношение 2, обладающее свойствами рефлексивности и антисиммет-
ричности и транзитивности: ( , )(( , ) 2&( , ) 2)
≡ называется отношением упорядоченности. Обозначается « ».
5.Отношение 2, обладающее свойствами антирефлексивности, антисимметричности и транзитивности называется отношением строгой упорядоченности. Записывается условие так: ( )(( , ) 2), ( , )(( , ) 2&( , ) 2) ≡ . Обозначается такое отношение
« ».
6.Отношение 2, обладающее свойствами рефлексивности и транзитивности называется отношением предпорядка.
7.Если отношение 2 рефлексивно и симметрично, то оно называется отношением толерантности.
Рассмотрим операцию включения: . Она рефлексивна – так как множество включает само себя. Она антисимметрична - & ≡. Значит, отношение включения является отношением упорядоченности.
Примером отношения строгой упорядоченности является отношение «<» на множестве рациональных чисел, а отношения предпорядка – отношение «Является делителем» для множества натуральных чисел.
15
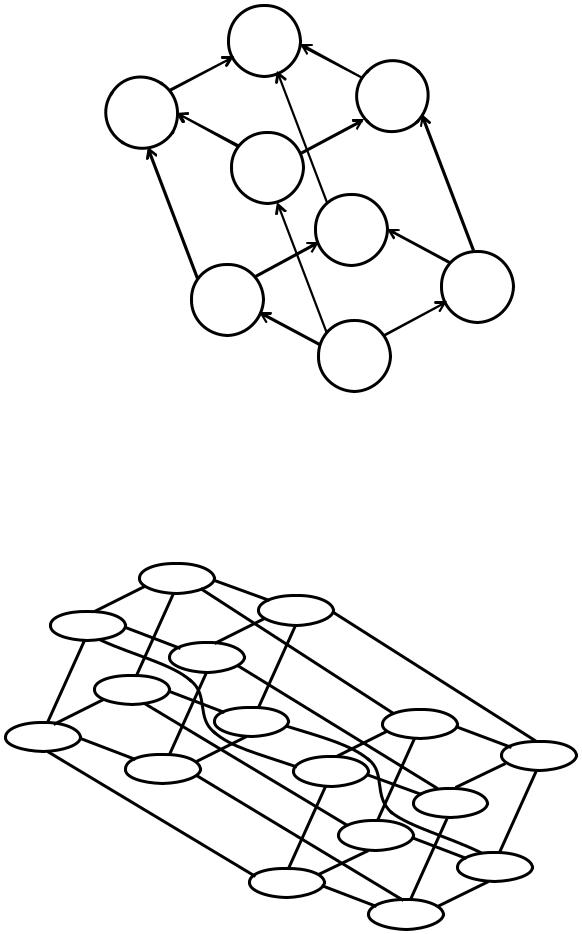
§4. ГРАФ ХАССЕ
Частично упорядоченные множества, обладающие графом = ; образуются из первоначального графа удалением всех петель и транзитивно замыкающих дуг. Такого вида граф называется графом Хассе (Hase). Граф Хассе (диаграмма Хассе) определяет базовое задание отношений упорядоченности на множестве.
Рассмотрим пример. Задан граф следующего вида:
{ , , }
{ , }
{ , }
{ }
{ , }
{ }
{ }
Рисунок 11
Граф Хассе для данного графа выглядит следующим образом:
16
{ , , }
{ , }
{ , }
{ }
{ , }
{ }
{ }
Рисунок 12
Внимательный человек без труда здесь заметит булеан третьей степени. В свою очередь булеан четвертой степени можно представить в виде декартова произведения булеана третьей степени на булеан первой:
111
111
110
110
101
100 |
|
101 |
|
011 |
|
|
|
||
|
|
|
|
|
|
100 |
|
010 |
011 |
|
|
|
||
|
|
|
|
|
|
|
|
|
010 |
|
|
|
|
001 |
|
|
|
000 |
001 |
|
|
|
|
|
|
|
|
|
000 |
|
|
|
Рисунок 13 |
|
|
|
|
17 |
|
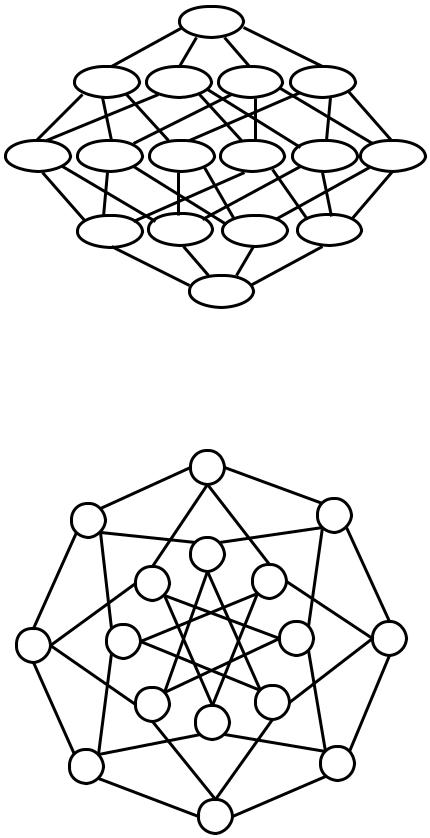
Либо в виде иерархичной структуры:
1111
1110 |
1101 |
1011 |
0111 |
1100 |
1010 |
0110 |
1001 |
0101 |
0011 |
1000 |
0100 |
0010 |
0001 |
0000
Рисунок 14
Есть ещё вариант представления булеана, в котором можно наблюдать возможность построения в формате, в котором длины рёбер булеана равны.
0000
|
1000 |
|
|
0001 |
|
|
|
|
|
|
|
|
1001 |
|
|
|
0100 |
0010 |
|
|
|
|
|
|
1100 |
1010 |
|
0101 |
0011 |
|
|
|
||
|
|
1101 |
1011 |
|
|
|
|
|
|
|
|
|
0110 |
|
|
1110 |
|
|
0111 |
1111
Рисунок 15
18
|
Говорят, |
что |
|
покрывает |
если: ( |
, ) || , |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть ( , ) и ′ , ′| ′: > , тогда называет-
ся мажорантой ′. Так же можно определить и миноранту.
Рассмотрим ′ = {( , ); ( , ); ( , , )}. Можно сказать, что
{ , } { } { } { } ( – является мажорантой).
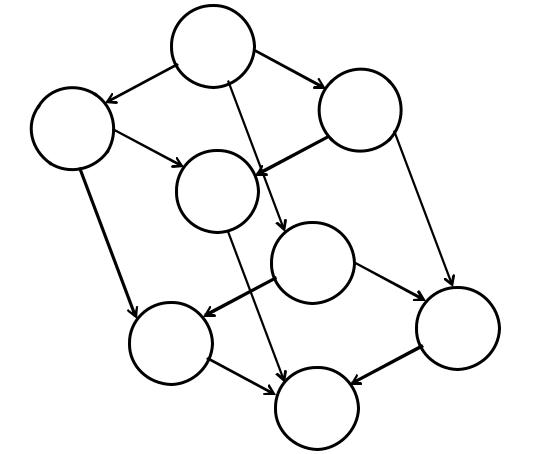
Двойственным частному упорядоченному множеству называется частично упорядоченное множество ̃, определённое на том же носителе с помощью обратного отношения. Обратным для графа Хассе будет отображение следующего вида:
{ , , }
{ , }
{ , }
{ }
{ , }
{ }
{ }
Рисунок 16
Принцип двойственности: Если теорема справедлива для частично упорядоченного множества с заданным отношением, она справедлива и для двойственного отношения к данному множеству.
19
§5. ВЗВЕШЕННЫЙ ГРАФ
Сопоставим каждой вершине |
|
|
̅̅̅̅̅ |
набор весов |
|
, = 1, |
|||
|
|
|
|
|
|
|
|
|
̅̅̅̅̅ |
Получим множество взвешенных вершин {( , ), = 1, }. |
||||
|
|
|
|
|
Определение |
|
|
|
|
Взвешенный граф – это набор: |
|
|
|
|
|
̃ |
|
|
|
( , ), ( , Φ) |
|
|||
{ ̃ |
|
|
|
. |
= = 1 |
|
|
||
̅̅̅̅̅.
, = 1,
(5.1)
Можно сказать, что это функция, определенная на вершинах и дугах графа. Имеем граф = , 1, 2′ , имеющий вершин и дуг. Будем считать:
1, если из дуги идет в |
|
|
|
|
|
|
|
|
|
= {−1, если это конец |
. |
|
|
(5.2) |
|
|
|
|
|
0, если не коинцидентна |
|
|
|
|
Соответственно, матрица инцидентности ( ) = [ |
] |
|
. Возникает в та- |
|
|
|
|
× |
|
|
|
|
|
|
кой матрице проблема при определении элементов – петель: в них элемент должен принимать значение «1» и «-1» одновременно, так как дуга выходит и возвращается в одну и ту же вершину.
Решением этой проблемы – разбить на + - начальную матрицу инцидентности и − - конечную матрицу инцидентности. Соответственно:
+ = [ + ] |
: + |
1, если |
− начало дуги |
|
|||
= { |
|
, |
|
||||
|
× |
|
0 − в противном случае |
|
|||
|
|
(5.3) |
|||||
|
|
|
|
|
1, если − конец дуги |
||
− = [ − |
] |
|
: − |
= { |
|
||
|
|
. |
|
||||
|
|
× |
|
|
0 − в противном случае |
|
|
|
|
|
|
|
|||
Для графа без петель: = + − − без учета весов вершин и дуг. Если же мы будем работать со взвешенным графом, то появятся ещё весовые матрица и вектор:
|
1 |
1 |
|
|
|
( ) = ‖ |
2 |
‖ ; Ρ( ) = ‖ |
2 |
‖. |
(5.4) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
