
шамин с сдо
.pdf
M = sup f(x)
[a,b]
[a, b]
xε [a, b]
f(x) |
[a, b] |
1
ϕ(x) = M − f(x) .
ε > 0
0 ≤ M − f(xε) < ε.
ϕ(xε) = |
1 |
> |
1 |
. |
|
|
|||
M − f(xε) |
ε |
|||
|
ϕ |
|
|
[a, b] |
xM [a, b]
f(xM ) = M.
m = inf f(x) −m = sup(−f(x))
[a,b] |
[a,b] |
|

xm [a, b] |
−f(xm) = |
−m
f(xm) = m.
|
f(x) |
[a, b] |
f(a) f(b) |
|
|
(a, b) |
|
c (a, b) |
f(c) = 0 |
|
|
|
[a, b] |
|
[a, b] |
f |
|
|
|
f(x) |
[a1, b1] |
|
|
x0 = (b1 − a1)/2 |
|
|
[a2, b2]
f(x)
[ak+1, bk+1] [ak, bk], k = 1, 2, . . . .

k |
|
|
|
|
|
|
|
|
|
|
|
|
b |
k − |
a |
k |
= |
b − a |
→ |
0, k |
→ ∞ |
. |
|
||
|
|
|
2k |
|
|
|
|
|||||
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
c |
|
||
f(x) |
|
|
|
|
|
|
|
|
|
|
|
ε |
|
U(c, ε) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
f(c) = 0 |
|
|
|
|
|||
|
|
|
|
|
|
f(x) |
|
|
|
|
[a, b] |
|
f(a) = A f(b) = B |
|
|
A 6= B |
|
C |
|
||||||
A B |
|
|
|
|
|
|
|
c (a, b) |
f(c) = C |
|||
|
|
|
|
|
|
|
|
|
|
F (x) = f(x) − C |
||
f(x) |
|
|
|
|
|
|
|
|
F (x) |
|
|
|
[a, b] |
|
|
|
F (x) |
|
|
|
|
|
|
[a, b] |
|
(a, b) |
|
|
|
c |
|
F (c) = 0 |
|
f(c) = C |
|
|||
f(x)
I
Yf = {f(x) : x I}
f(x)
x I
Yf
f−1
Yf
[a, b]
f−1
f(x)
y Yf |
|
y = f(x) |
f(x) |
I
f−1(x)
x = f−1(f(x)), x = f(f−1(x)).
(x)
I
f(x)
[A, B] |
A = f(a) B = f(b) |
|
y [A, B] |
|
|
x |
[a, b] |
x |
|
x′ |
|
[a, b] |
f(x′) = y |
x′ = x |
x′ |
|
|
|
6 |
|
|
|
x |
|
x′ < x |
x′ > x |
|
f(x′) < f(x) |
f(x′) > f(x) |
|
|
||
f(x′) = y = f(x)
f(x)

y0
(A, B) |
x0 = f−1(y0) (a, b) |
ε > 0 |
[x0 − ε, x0 + ε] [a, b].
ya = f(x0 − ε) yb = f(x0 + ε)
y0 (ya, yb) |
δ > 0 |
(y0 − δ, y0 + δ) (ya, yb). |
|
f−1((y0 − δ, y0 + δ)) f−1((ya, yb)) = (x0 − ε, x0 + ε). y0 = A y0 = B
|
f(x) |
|
I R |
g(x) |
J R |
|
g(x) |
|
|
Yg I, |
|
|
|
h(x) = f(g(x)) |
|
J |
|
|
f(x) |
[a, b] |
|
g(x) |
[c, d] |
|
g(x) |
[a, b] |
h(x) = f(g(x))

[c, d]
x0 [c, d]
xx0+Δx [c, d]
g(x) |
g |
g → 0, |
x → 0. |
g |
f(x) |
|
f(x) |
f → 0, |
g → 0. |
h → 0, x → 0.
h(x)
f(x)
x0
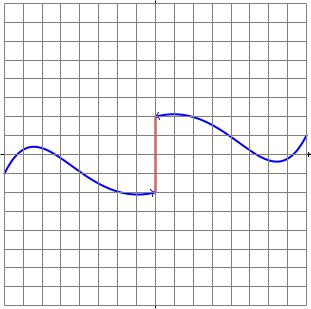
f(x)
x0 |
x0 |
x0
x0
f(x)
x0
c = lim f(x) − lim f(x)
x→x0+0 x→x0−0
x0
x2 
c
x1
|
|
|
f(x) |
|
x0 |
|
|
|
x0 |
x0 |
|
|
|
lim f(x) |
|
|
|
|
x→x0+0 |
lim |
0 f(x) |
|
±∞ |
|
x x0 |
− |
|
||
→ |
|
|
|
|
|
|
|
|
f(x) = c |
|
|
|
|
x |
|
|
y = c − c = 0. |
||
|
|
f(x) = x |
R |
|
|
|
y = |
x → 0, |
x → 0. |
|
|
|
Pn(x) |
|
|
|
sin x |
cos x |
tg x ctg x |
|
|
|
|
sin x |
| sin x| < |x|.

| sin x| |
1 |
|x| < |
π/2 |
|x| |
|x| | sin x|
x −x
lim sin x = 0.
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
x |
|
|
|
|
|
sin x |
|
|
|
sin |
|
|
|
· cos x0 |
|
|
|
|
|
x→0 |
− |
|
x→0 |
|
|
2 |
+ 2 |
|
= 0. |
||||
lim [sin(x + x) |
|
sin x] = 2 |
lim |
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
cos x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
sin x |
|
|
|
|
|
R |
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x = sin x + |
π |
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|||||
tg x |
ctg x |
|
|
|
|
|
|
|
|
|
|
|
|
sin x < x < tg x, x 0, |
π |
, |
|
||
2 |
cos x < sin x < 1. x
cos x |
sin x |
|
|
x |
|
||
|
|
||
|
0 < |x| < π2 |
||
x → 0 |
|
lim cos x = 1 |
|
|
x 0 |
||
cos x |
|
→ |
|
|
|
||
|
lim |
sin x |
= 1. |
|
x |
||
|
x→0 |
|
|
arcsin x, arccos x, arctg x
