людкоский тарф методичка с сдо

Предполагаем, что t-номер машины Тьюринга M, которая чисто вычисляет n-местную функцию f. Для доказательства теоремы введем (n+2)-местную функцию

Sn,t (X1, …, Xn, y,z) =

0, если М проводит конфигурацию 1 ≠ 1 □ 2□ … □

{в конфигурацию. . . 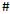0 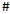. . . за ≤ шагов,

1, в противном случае

Сначала установим, что эта функция Sn,t примитивно-рекурсивна.

Лемма 1. Функция Sn,t является примитивно-рекурсивной.

Доказательство. Сначала заметим, что Sn,t (x1, …, xn, y, z) = 0 при j ≤ z, где j

– наименьшее натуральное число, такое, что w(t, γn(x1, …, xn,j)) является номером конфигурации вида #...#q0#y#...#, так как согласно предложению 11 число w(t, γn(x1, …, xm,j)) будет номер конфигурации, в которую машина Тьюринга М перерабатывает исходную конфигурацию q1#x1□x2□…□xn за j шагов.

Для конфигурации вида #...#q0#y#...# с номером w(t, γn(x1, …, xn,j)) вы-

полняется равенство ex(1, w(t ( 1, … , , )) = 0, а также

2( (3, ( , ( 1, … , )) = –число единиц в рассматриваемой конфигурации. Отсюда вытекает, что ,( 1, … , , , ) = 0 равносильно тому, что

≤ [ (1, (t ( 1, … , , )) + | 2( (3, ( , ( 1, … , )) − | = 0] ≤ ,

что в свою очередь равносильно условию ≤ [ (1, (t ( 1, … , , )) + | 2( (3, ( , ( 1, … , ),3) − | = 0] = 0, отсюда получаем представление ,( 1, … , , , ) = ≤[ (1, (t ( 1, … , , )) +

| 2( (3, ( , ( 1, … , ),3) − | = 0] , следовательно, , является при-

митивно-рекурсивной функцией.

Окончательное доказательство теоремы 2.

Зададим теперь (n+3) – местную функцию Sn,t (t1, x1, …, xn, y, z) = Sn,t (x1, …, xn, y , z). В силу леммы 1 функция Sn примитивно-рекурсивна. Также опреде-

лим еще (n+2) – местную функцию Tn(t,x1,…, xn, z) = Sn(t,x1,…,xn,l(z),r(z)), где z-

номер пары (a,b) с l(z)=a, r(z)=b согласно нумерующей функции Кантора для пар неотрицательных целых чисел. Очевидно, что функция Tn тоже примитивно-ре- курсивна. Тогда Tn(t1,x1,…xn,z)=0 равносильна тому, что вычисление функции f машиной Тьюринга M с номером t заканчивается за число шагов не превосходящего r(x) с результатом l(x). В противном случае получим Tn(t1,x1,…xn,z)=1. Если

61

t-фиксированный номер, то положим для простоты рассмотрения F(x1,…xn,z)= Tn(t1,x1,…xn,z)

Предположим, что значение f(x1,…xn) определено и f(x1,…xn)=y. Тогда вычисление на машине Тьюринга M заканчивается за некоторое конечное число K шагов, причем c(y,k) – наименьшее значение z, для которого Tn (t,x1,…xn,z)=0,

следовательно, F(x1,…xn,z)=0 и y=l( z[F(x1,…xn,z)=0]).

Пусть теперь значение l( z[F(x1,…xn,z)=0]) определено и равняется y, следовательно, F(x1,…xn,z)=0, где z=c(y,k) для некоторого число k. Итак, в этом случае Tn (t,x1,…xn,z)=0 и вычисление f(x1,…xn) на машине Тьюринга М оканчивается на k-м шаге с результатом y, то есть f(x1,…xn)=y. Таким образом, для функции F выполняется утверждение данной теоремы.

Определение 8. Для семейства F n-местных частичных числовых функций, если имеется (n+1) – местная функция u, которая удовлетворяет условиям (1) и

(2):

(1)f(x1,…xn) u(j,x1…,xn) принадлежит F для всякого j;

(2)f(f F)j x1…xn f((x1,…xn) ) u(j,x1…,xn),

то u называется универсальной функцией для семейства F.

Теорема 3. Если Fn – семейство всех n-местных частично-рекурсивных функций, где n-натуральное число, n=1,2…, то существует (n+1) – местная ча- стично-рекурсивная функция un, которая универсальна для Fn.

Доказательство. Зададим частично-рекурсивную функцию un(t,x1…xn) l( z[Tn(t,x1,…xn,z)=0]). Если t фиксировано, то un как функция переменных x1,…,xn задает n – местную частично-рекурсивную функцию, следовательно условие (1) из определения 8 выполнено. В силу теоремы 1 для произвольной частично-рекурсивной функции существует некоторая машина Тьюринга M с номером t, которая вычисляет f. Из доказательства предыдущей теоремы вытекает, что выполняется условное равенство (x1,…xn) un(t,x1…,xn), следовательно условие (2) из определения 8 тоже выполнено.

нумерующей функции Кантора для пар неотрицательных чисел. Очевидно, что

62

функция тоже примитивно-рекурсивна. Тогда ( , 1, … , , ) = 0 равносильна тому, что вычисление функции f машиной Тьюринга М с номером t заканчивается за число шагов не превосходящего r(x) с результатом l(x). В противном случае получим ( , 1, … , , ) = 1. Если t-фиксированный номер, то положим для простоты рассмотрения F( 1, … , , )= ( , 1, … , , )

Предположим, что значение f( 1, … , ) определено и f( 1, … , ) = . Тогда вычисление на машине Тьюринга М заканчивается за некоторое конечное

Получается условное равенство ( 1, … , ) = ( , 1, … , ), следовательно условие (2) из определения 8 тоже выполнено.

63

Литература.

1)Мальцев А.И. Алгоритмы и рекурсивные функции. - М.: Наука, 1986, -

368 с.

2)Крупский В.Н., Плиско В.Е. Математическая логика и теория алгоритмов.

- М.: Академия, 2013. – 416 с.

3)Мендельсон Э. Введение в математическую логику. - М.: Наука, 1984. – 320 с.

4)Яблонский С.В. Введение в дискретную математику. - М.: Высшая Школа, 2002. – 384 с.

5)Гаврилов Г.П, Сапоженко А.А. Задачи и упражнения по дискретной мате-

матике. - М.: Наука, 2006. – 416 с.

6)Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: Наука, 1975. – 240 с.

7)Справочная книга по математической логике. Часть III. Теория рекурсии / под ред. Дж. Барвайса. – М.: Наука, 1982. – 360 с.

8)Шенфилд Дж. Математическая логика. – М.: Наука, 1975. – 528 с.

9)Кормен Т.Х., Лейзерсон Ч.И., Ривест Р.Л., Штайн К. Алгоритмы: построение и анализ. - М.: «Вильямс», 2019. - 1328 с.

64