Решение

Поскольку отказ устройства происходит при отказе любого его элемента, имеет место последовательное соединение элементов. Поэтому интенсивность отказов устройства λ равна сумме интенсивностей отказов всех его элементов, иными словами:

λ = ∑ λ_i n_i = λ₁n₁ + λ₂n₂ + λ₃n₃ + λ₄n₄=255·10^–10 + 32·10^-9 + 42·10^-8 + 11·10^–7ч^–1= = 1,5775·10^–6 ч^–1.

Поскольку интенсивности отказов всех элементов постоянны (не зависят от времени), постоянна и интенсивность отказов устройства. Поэтому распределение наработки до отказа является экспоненциальным, т.е. вероятность безотказной работы выражается формулой P(t) = e^{– λt}.

Для средней наработки устройства до отказа имеем:

T = 1/λ = 1/(1,5775·10^–6) = 633914,422 ч.

Если t = 2 года = 2·365·24 ч = 17520 ч, то λt=1,5775·10^–6·17520 = 0,027638, откуда получим вероятность безотказной работы в течение двух лет:

P(2 года) = e^{– λt} = e^–0,027638 = 0,972741.

Ответ: T = 633914,422 ч; P(2 года) = 0,972741.

Задача 3

Сеть связи имеет структуру, изображенную на рисунке 1 («мостик с двумя перемычками»). Рассматривается связь между двумя полюсами сети (выделены на рисунке заливкой). Предполагается, что связь возможна, если между полюсами сети существует работоспособный путь. Состояния всех линий независимы, узлы считаются абсолютно надежными. Вероятности работоспособности линий p_i (i = 1,…,6) для каждого варианта даны в таблице 3.

Рассчитать вероятность работоспособности (возможности связи между полюсами) сети, используя разложения по элементам.

Перечислить все простые пути и простые сечения системы.

Рассчитать нижнюю и верхнюю оценки вероятности работоспособности системы на основе попарно непересекающихся простых путей и сечений (оценки Литвака-Ушакова).

Рисунок 1 - Схема сети связи («мостик с двумя перемычками»)

Таблица 3 – Вариант исходных данных к заданию 3

Номер варианта	Вероятность pi
	для i ≠ 3, 6	для i = 3, 6
20	0,95	0,99

Решение

В качестве элемента разложение берутся перемычки – элементы 3 и 6. Обозначим через A событие работоспособности системы. При разложении по двум элементам возможны четыре следующих ситуации: x₃ = 0 и x₆ = 0; x₃ = 0 и x₆ = 1; x₃ = 1 и x₆ = 0; x₃ = 1 и x₆ = 1. Для его вероятности имеет место равенство:

P = P(A) = (1 – p₃) (1 – p₆)P{A  x₃ = 0 x₆ = 0} + (1 – p₃)p₆P{A  x₃ = 0 x₆ =

= 1} + p₃ (1 – p₆)P{A  x₃ = 1 x₆ = 0} + p₃ p₆P{A  x₃ = 1 x₆ = 1}.

Условие неработоспособности элемента разложение приводит к удалению соответствующего ребра из графа, а условие работоспособности элемента разложение – к стягиванию его граничных вершин. При разложении по двум элементам, как уже было сказано, всего возможны четыре следующих ситуации: x₃ = 0 и x₆ = 0; x₃ = 0 и x₆ = 1; x₃ = 1 и x₆ = 0; x₃ = 1 и x₆ = 1. При этом получаются системы, изображенные на рисунках 2а, 2б, 2в и 2г соответственно. Они являются приводимыми, расчёт вероятностей их работоспособности P₀₀, P₀₁, P₁₀ и P₁₁ осуществляется на основе формул для последовательного и параллельного соединений.

Первая система представляет собой параллельное соединение двух модулей (рисунок 2а), первый из которых – последовательное соединение элементов 1, 4 и 7, второй – последовательное соединение элементов 2, 5 и 8. Для первого модуля p₁₄₇ = p₁p₄p₇, для второго p₂₅₈ = p₂p₅p₈, откуда:

P₀₀ = 1 – (1 – p₁₄₇) (1 – p₂₅₈) = p₁p₄p₇ + p₂p₅p₈ – p₁p₄p₇p₂p₅p₈ = 0,979658.

Вторая система представляет собой последовательное соединение двух модулей (рисунок 2б), первый из которых – параллельное соединение последовательной цепи из элементов 1 и 4 и последовательного соединения из элементов 2 и 5, а второй модуль – параллельное соединение элементов 7 и 8.

Тогда для первого модуля:

p₁₄₂₅ = 1 – (1 - p₁₄)(1 – p₂₅) = p₁₄ + p₂₅ – p₁₄p₂₅ = p₁p₄ + p₂p₅ – p₁p₄p₂p₅,

для второго модуля:

p₇₈ = 1 – (1 – p₇)(1 – p₈) = p₇ + p₈ – p₇p₈,

откуда:

P₀₁ = p₁₄₂₅ p₇₈ = (p₁p₄ + p₂p₅ – p₁p₄p₂p₅)(p₇ + p₈ – p₇p₈) = 0,988018.

Третья система представляет собой последовательное соединение двух модулей (рисунок 2в), первый из которых – параллельное соединение элементов 1 и 2, а второй модуль – параллельное соединение последовательной цепи из элементов 4 и 7 и последовательного соединения из элементов 5 и 8.

Для первого модуля:

p₁₂ = 1 – (1 – p₁)(1 – p₂) = p₁ + p₂ – p₁p₂,

для второго модуля:

p₄₇₅₈ = 1 – (1 – p₄₇)(1 – p₅₈) = p₄₇ + p₅₈ – p₄₇p₅₈ = p₄p₇ + p₅p₈ – p₄p₇p₅p₈,

откуда:

P₁₀ = p₁₂ p₄₇₅₈ = (p₁ + p₂ – p₁p₂)(p₄p₇ + p₅p₈ – p₄p₇p₅p₈) = 0,988018.

Четвертая система представляет собой последовательное соединение трех модулей, первый из которых – параллельное соединение элементов 1 и 2, второй – параллельное соединение элементов 4 и 5, а третий – параллельное соединение элементов 7 и 8. Для первого модуля:

p₁₂ = 1 – (1 – p₁)(1 – p₂) = p₁ + p₂ – p₁p₂,

для второго:

p₄₅ = 1 – (1 – p₄)(1 – p₅) = p₄ + p₅ – p₄p₅,

для третьего:

p₇₈ = 1 – (1 – p₇)(1 – p₈) = p₇ + p₈ – p₇p₈,

откуда:

P₁₁ = p₁₂ p₄₅ p₇₈ = (p₁ + p₂ – p₁p₂)(p₄ + p₅ – p₄p₅)( p₇ + p₈ – p₇p₈) = 0,992519.

Окончательный результат:

P = (1 – p₃)(1 – p₆)P₀₀ + (1 – p₃)p₆P₀₁ + p₃ (1 – p₆) P₁₀ + p₃ p₆ P₁₁ =(1 – p₃)(1- – p₆)(p₁p₄p₇ + p₂p₅p₈ – p₁p₄p₇p₂p₅p₈) +(1 - p₃)p₆(p₁p₄ + p₂p₅ – p₁p₄p₂p₅) *

* (p₇ + p₈ – p₇p₈)P₀₁ + p₃ (1 – p₆)(p₁ + p₂ – p₁p₂)(p₄p₇ + p₅p₈ – p₄p₇p₅p₈) +

+ p₃p₆(p₁ + p₂ – p₁p₂)(p₄ + p₅ – p₄p₅)( p₇ + p₈ – p₇p₈) = 0,01·0,01·0,979658 + 

+ 0,01·0,99·0,988018+ 0,99·0,01·0,988018+ 0,99·0,99·0,992519 = 0,992428.

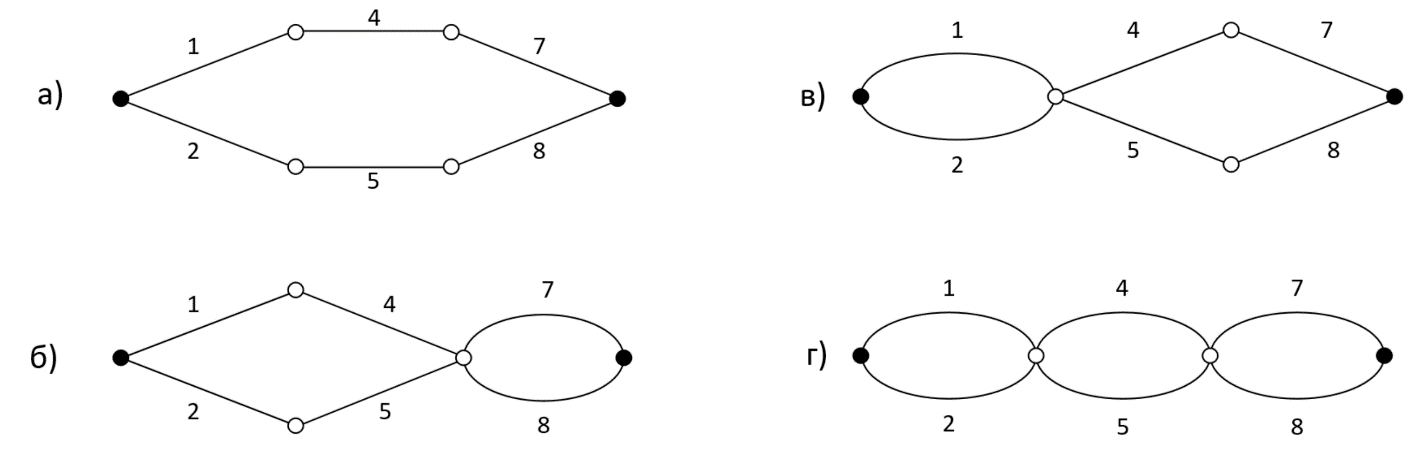
Рисунок 2 - Системы, полученные при разложении мостика и используемые для получения нижней и верхней оценок

Все простые пути мостика: {1, 4, 7}, {2, 5, 8}, {1, 3, 5, 8}, {2, 3, 4, 7}, {1, 4, 6, 8}, {2, 5, 6, 7}, {1, 3, 5, 6, 7}, {2, 3, 4, 6, 8}.

Все простые сечения мостика: {1, 2}, {4, 5}, {7, 8}, {1, 3, 5}, {2, 3, 4}, {4, 6, 8}, {5, 6, 7}, {1, 3, 6, 8}, {2, 3, 6, 7}.

Для расчёта нижней оценки вероятности работоспособности берём попарно непересекающиеся простые пути {1, 4, 7}, {2, 5, 8}, соединяя их параллельно (рисунок 2а). Вероятность работоспособности получившейся системы есть рассчитанная выше вероятность P₀₀, откуда P_н = P₀₀ = 0,979658.

Для расчёта верхней оценки вероятности работоспособности берём попарно непересекающиеся простые сечения {1, 2}, {4, 5}, {7, 8}, соединяя их последовательно (рисунок 2г). Вероятность работоспособности получившейся системы есть рассчитанная выше вероятность P₁₁, откуда P_в = P₁₁ = 0,992519.

Убеждаемся, что P_н < P < P_в: 0,979658 < 0,992428 < 0,992519.

Ответ: P = 0,992428; P_н = 0,979658; P_в = 0,992519.