
- •3Лек. Понятия свертки и скалярного произведения двух непрерывных сигналов, норма сигнала и взаимная ортогональность сигналов. Спектр свертки, классическое и обобщенное равенства Парсеваля.
- •5Лек. Спектральная классификация непрерывных вещественных сигналов: нч сигнал, пч, шпч, упч –сигналы, вч-сигнал, чо-сигнал. Ответ пояснить соответствующими графиками спектров сигналов.
- •9Лек. Центрированный прямоугольный импульс единичной амплитуды, длительности т, его комплексный спектр, спектральная плотность энергии и корреляционная функция. Изобразить их графики.
- •18Лек. Спектральная классификация линейных фильтров – понятия фнч, фпч, фвч, упч, шпч, чо-фильтр, рч-фильтр. Ответ пояснить соответствующими графиками ачх фильтров.
9Лек. Центрированный прямоугольный импульс единичной амплитуды, длительности т, его комплексный спектр, спектральная плотность энергии и корреляционная функция. Изобразить их графики.
Центрированный прямоугольный импульс единичной амплитуды и длительности Т.

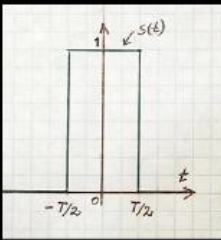
Комплексный спектр вычисляем с непрерывным преобразованием Фурье (НПФ), из-за четности сигнала, спектр вещественен.

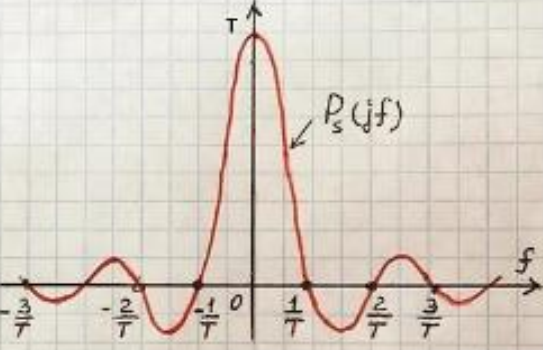
Спектральная плотность энергии (СПЭ)
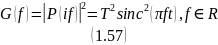
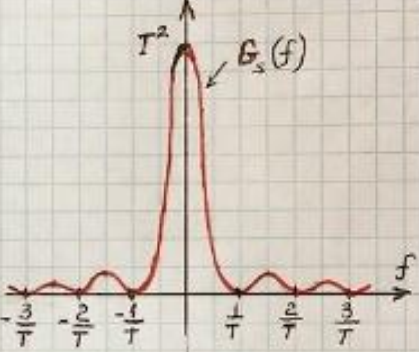
Корреляционная функция (КФ) вычисляется по (1.30)
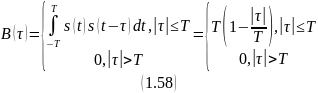
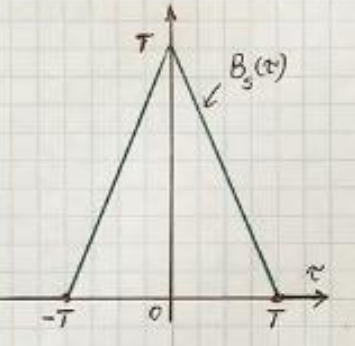
Особенности прямоугольного импульса:
 главный лепесток
локализован на
главный лепесток
локализован на
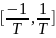 .
.
Максимум
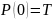 ,
при f=0.
,
при f=0.
Нули в точках
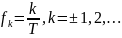
“Хвосты” кривой
медленно спадают по амплитуде, поэтому

График
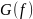 спадает гораздо быстрее, чем график
спектра
спадает гораздо быстрее, чем график
спектра
 ,
но точки прохождения через 0 у них
совпадают.
,
но точки прохождения через 0 у них
совпадают.
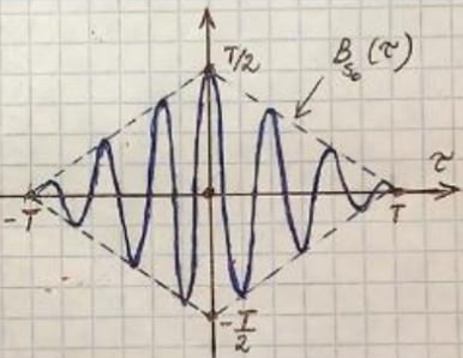
График КВ
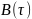 по форме является треугольным импульсом,
у которого:
по форме является треугольным импульсом,
у которого:длительность в два раза больше, чем у исходного
амплитуда в T раз больше, чем у исходного
Там есть еще какой-то треугольный импульс, но его нет в вопросах, он видимо ущербный какой-то.
10Лек. Полосовой сигнал с центрированной прямоугольной огибающей единичной амплитуды, длительности Т, его комплексный спектр, спектральная плотность энергии и корреляционная функция. Изобразить их графики.
Полосовой
сигнал s0(t)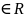 с прямоугольной огибающей:
с прямоугольной огибающей:
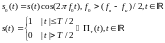
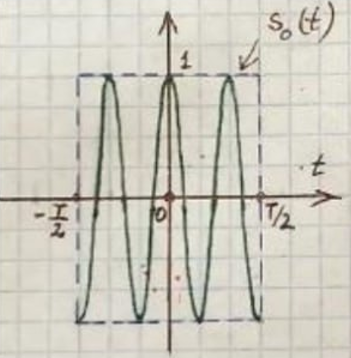
Комплексный спектр:

Где нижняя и верхняя частоты fн, fв НЧ сигнала s(t) определяются по энергетическому критерию.
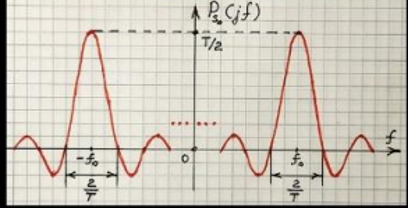
СПЭ:
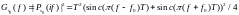
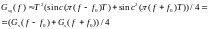
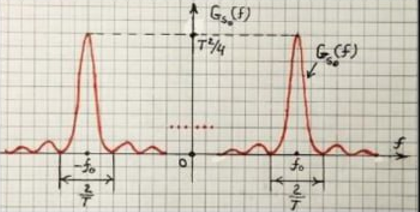
Корреляционная функция:
С помощью теормы Винера Хинчина

11Лек. Определение функции Дирака, ее интерпретация как предел последовательности нормированных финитных функций с конечной энергией (на примере двух однопараметрических семейств), вычисление комплексного спектра функции Дирака на основе данной интерпретации. Ответ пояснить графиками.
Определение функции Дирака
Дельта-функция
Дирака D(x)
для любого вещественного аргумента

Определяется
двумя соотношениями

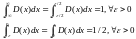 (условие
нормировки)
(условие
нормировки)
где
условие нормировки означает, что интеграл
от дельта-функции равен 1 на любом сколь
угодно малом симметричном интервале
(- ).
).
Комплексный спектр дельта-функции
Комплексный
спектр PD(jf)
дельта-функции Дирака D(x)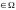 ’
равен 1, т.е. PD(jf)=F(D(x))=1,
f
’
равен 1, т.е. PD(jf)=F(D(x))=1,
f
Доказательство:
с учетом асимптотической аппроксимации
D(x)=
Имеем
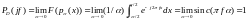
Физическая интерпретация:
дельта-функция
D(x)
можно представить как предел
 ,
,

Бесконечной
последовательности непрерывных функций
 с конечной энергией
с конечной энергией
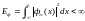 ,
зависящих от параметра a>0
и удовлетворяющих условию нормировки
.
,
зависящих от параметра a>0
и удовлетворяющих условию нормировки
.
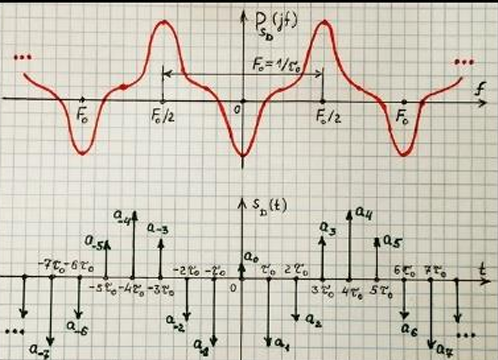
Спектр линейной комбинации дельта-импульсов
12Лек. Определение функции Дирака, функции Хевисайда и интегральная связь между ними. Свойства сдвинутой дельта-функции Дирака – ее спектр и представление через прямое/обратное преобразование Фурье. Фильтрующее свойство дельта функции Дирака. Спектры сигнала-константы, комплексного гармонического сигнала и соответствующие графики.
(1.20) Дельта-функция Дирака
Дельта-функция Дирака D(x) для любого вещественного аргумента x∈ℝ определяется двумя соотношениями:
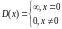 (1.73a)
(1.73a)
Условие нормировки:
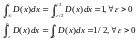 (1.73б)
(1.73б)
где условие нормировки означает, что интеграл от дельта функции равен 1 на любом сколь угодно малом симметричном интервале (-е/2, е/2).
Функция Хэвисайда
представляет собой сигнал в виде единичного скачка:
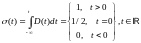
Который
можно подставить в суммы .
Поэтому с учетом (1.87)
.
Поэтому с учетом (1.87)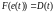 и формулы (1.94) спектр функции Хэвисайда
и формулы (1.94) спектр функции Хэвисайда

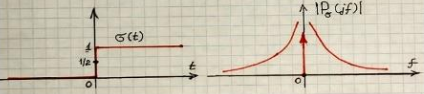
Свойства сдвинутой дельта-функции Дирака:
Применим обратное преобразование Фурье к обеим частям равенства (1.82) и учтем свойство четности функции Дирака D(x-x0)=D(-(x-x0))
 (1.83)
(1.83)
Спектр сдвинутой дельта-функции Дирака:

Фильтрующее свойство дельта функции Дирака:
Для любой
непрерывной комплексной функции
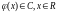 с
конечной энергией и дельта-функциец
Дирака D(x)
справедливо
с
конечной энергией и дельта-функциец
Дирака D(x)
справедливо
 (1.81)
(1.81)
Док-во: Это свойство непосредственно следует из формулы для свертки (1.80) где х=х0.
(!!) равенство (1.81) физически трактуется: любое значение фи(х0) функции(сигнала) фи(х) можно получить, пропустив ее через фильтр с импульсной характеристикой D(x-x0) - используется для описания дискретизации сигнала.
Спектры сигнала-константы:
В частности при k=0 получаем сигнал в виде единичной констаны e(t), t принадлежит к действ.числам спектр которого согласно (1.86) имеет вид дельта-функции, локализованной на нулевой частоте, т.е справедливо
 (1.87)
(1.87)
Спектр комплексного гармонического сигнала:
Пусть в равенстве
 (1.84а)
(1.84а)
Переменные
х,х0 являются частота f,
kf0
принадлежащим к действ. числам R,
где k
принадлежит целым числам Z,
а переменная f
описывает время t.
Тогда делая замену переменных с х на f
и записывая (1.84а) справа налево, спектр
комплексного гармонического сигнала ,
где t
принадлежит действ.числам равен
,
где t
принадлежит действ.числам равен
 (1.86)
(1.86)

Т.е совпадает с дельта-функцией Дирака, локализованной в точке f=kf0.
13Лек. Вычисление спектра вещественного гармонического сигнала, спектра периодического сигнала, спектра последовательности дельта-импульсов, спектр функции Хевисайда. Изобразить соответствующие графики сигналов и спектров.
Спектр вещественного гармонического сигнала (1.88):
Рассмотрим вещественный гармонический сигнал в виде косинусоиды
 .
Тогда его комплексный спектр
.
Тогда его комплексный спектр
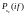 можно
найти как предельный вариант спектра
можно
найти как предельный вариант спектра
 полосового
сигнала
полосового
сигнала с
прямоугольной огибающей s(t),
когда его длительность T
стремится к бесконечности. В результате
получаем:
с
прямоугольной огибающей s(t),
когда его длительность T
стремится к бесконечности. В результате
получаем:

Предельные
функции стремятся к смещенным на
 дельта-функциям.
дельта-функциям.
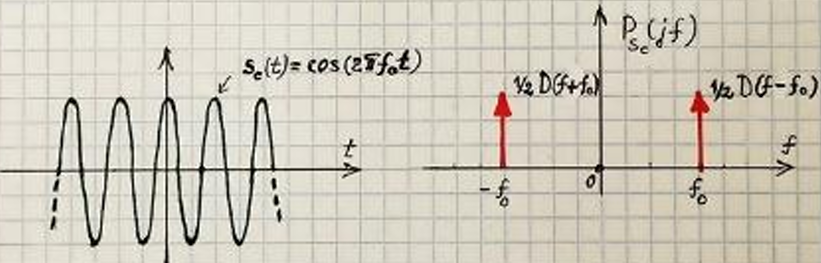
Рис. 7 График вещественного гармонического сигнала и его спектра.
Спектр периодического сигнала (1.90):
*есть еще напоминание что такое периодический сигнал, если надо - впишу*
Любой
периодический сигнал можно разложить
в комплексный ряд Фурье по комплексным
гармоникам
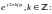
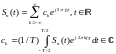
 - частота первой
гармоники ряда
- частота первой
гармоники ряда
Применим
к обеим частям преобразование Фурье,
тогда с учетом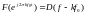 получим:
получим:
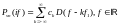
Спектр периодического сигнала в общем случае – бесконечная линейная комбинация сдвинутых по частоте дельта функций.
*причем
для вещественного периодического
сигнала
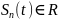 выполняется
выполняется
 .
.
*а
если сигнал вещественный и четный, то
 ,
а спектр также
становится вещественным и четным.
,
а спектр также
становится вещественным и четным.
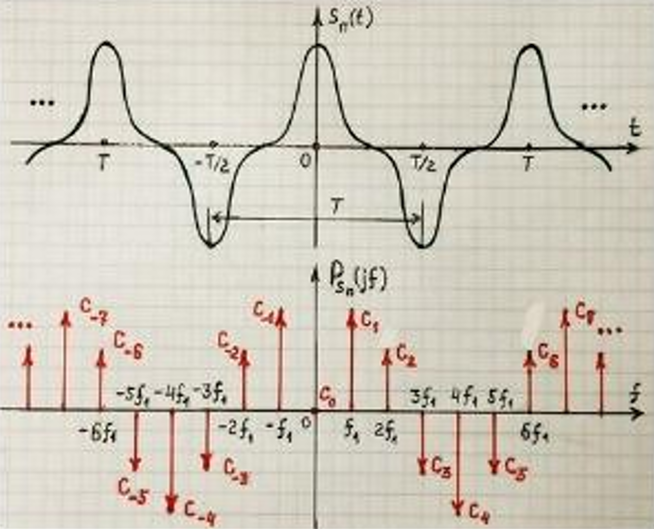
Рис. 8 График периодического сигнала и его спектра.
Спектр последовательности дельта-импульсов (надеюсь это оно) -спектр линейной комбинации дельта-импульсов (1.92):
Сигнал в виде линейной комбинации сдвинутых дельта-импульсов имеет вид
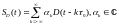
Применив
к обеим частям преобразование Фурье и
воспользовавшись свойством
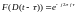 находим спектр
сигнала SD
(t):
находим спектр
сигнала SD
(t):
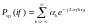
*он
представляет линейную комбинацию
комплексных гармоник
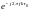 ,
а значит является периодической
комплексной функцией частоты с периодом
,
а значит является периодической
комплексной функцией частоты с периодом
 .
При
.
При
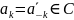 периодический спектр становится
вещественным, а при
периодический спектр становится
вещественным, а при
 вещественными оказываются и сигнал
вещественными оказываются и сигнал
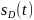 и его спектр.
и его спектр.
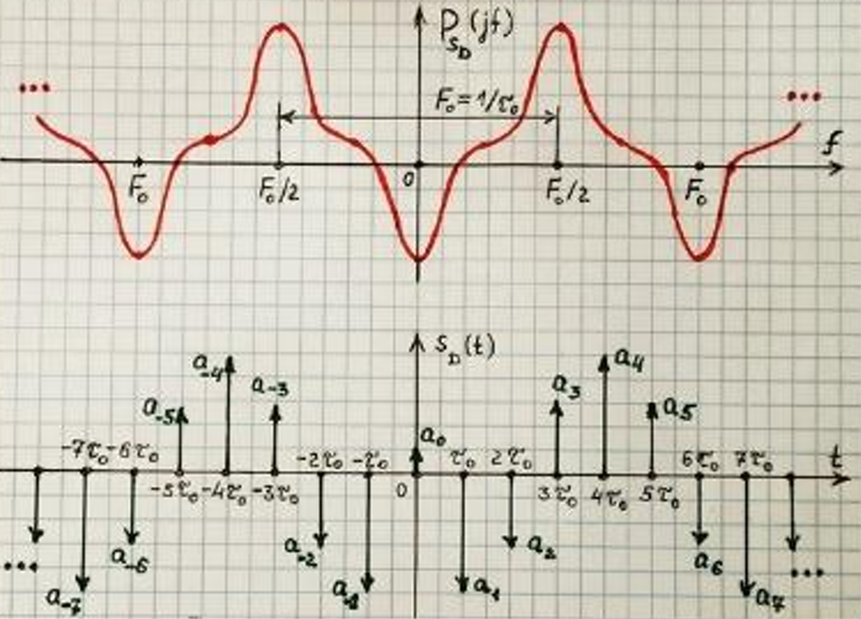
Рис. 9 График линейной комбинации дельта-импульсов и ее спектра.
Спектр функции Хевисайда (1.96):
Функция Хэвисайда представляет собой сигнал в виде единичного скачка:
Который
можно подставить в суммы
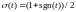 .Поэтому
с учетом
.Поэтому
с учетом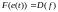 и
формулы (1.94 комплексный спектр функции
знака):→
и
формулы (1.94 комплексный спектр функции
знака):→

→Спектр функции Хэвисайда равен:


Рис. 10 График функции Хэвисайда и ее спектра
14Лек. Определения: линейной непрерывной системы (л.н.с), импульсной характеристики (ИХ), переходной характеристики (ПХ) и устойчивости л.н.с. Как найти сигнал на выходе л.н.с. по известному входному. Как оценить устойчивость по виду ИХ и ПХ.
Определение линейной непрерывной системы (л.н.с):
Линейной непрерывной системы называют устройство, действие которого на вх. Непрерывные сигналы описывается линейным оператором L(∙), т.е. удовлетворяет условию линейности
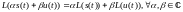
где s(t) и u(t) ∈ С = непрерывные комплексные сигналы
Определение импульсной характеристики (ИХ) л.н.с
ИХ или реакцией g(t) л.н.с L(∙) называется ее отклик на дельта-импульс Дирака D(t), т.е

Определение переходной характеристики (ПХ) л.н.с
ПХ л.н.с называется ее отклик на входное воздействие в виде единичного скачка Ϭ(t) функции Хэвисайда
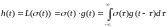
Определение устойчивости и неустойчивости л.н.с
Линейная непрерывная система L(∙) называется устойчивой, если при любом ограниченном вх.воздействии s(t) ∈ С: |s(t)| < ps < ∞, t ∈ R ее отклик x(t)= L(s(t)) также ограничен, т.е. x(t) ∈ С: |x(t)| < px < ∞, t ∈ R
Если же отклик x(t) не ограничен, то система называется неустойчивой
ИХ устойчивой л.н.с. удовлетворяет условию
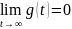
ПХ НЕустойчивой л.н.с. удовлетворяет условию
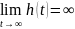
Нахождение сигнала на выходе:
Теорема (аналитическое описание л.н.с.)
Любой ограниченный линейный оператор L(∙) можно задать в явном виде через его импульсную характеристику g(t) по формуле
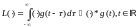 Выражение
означает, что для
нахождения сигнала x(t)
на выходе любой устойчивой линейной
системы с известной ИХ g(t)
= L(D(t))
достаточно вместо (∙) подставить
вх.сигнал
s(τ)
∈
С и
вычислить
полученный интеграл свертки,
т.е
Выражение
означает, что для
нахождения сигнала x(t)
на выходе любой устойчивой линейной
системы с известной ИХ g(t)
= L(D(t))
достаточно вместо (∙) подставить
вх.сигнал
s(τ)
∈
С и
вычислить
полученный интеграл свертки,
т.е
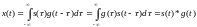
15Лек. Определение линейного непрерывного фильтра и генератора как частных случаев л.н.с. Принцип причинности и понятие физически реализуемого фильтра. Задача синтеза оптимального фильтра и понятие формирующего фильтра.
Линейный фильтр – устойчивая л.н.с. (линейная непрерывная система).
Генератор – неустойчивая л.н.с., у которой ИХ g(t) является периодической функцией.
Принцип причинности:
Любая физически реализуемая система не может порождать отклик, начинающийся раньше момента приложения воздействия.
Физическая реализуемость фильтров:
Линейный фильтр называется физически реализуемым, если его импульсная реакция g(t) удовлетворяет условиям:

То есть ИХ равна 0 при отрицательны значениях t<0, а ее энергия Eg конечна.
Задача синтеза оптимального фильтра:
«найти
оптимальную импульсную характеристику
фильтра g0(t) K
при которой в случае подачи на его вход
казуального сигнала s(t)
)
K
сигнал x(t)=s(t)*g(t)
на его выходе наилучшим образом приближает
некоторый желаемый сигнал xж(t)
)
K,
то есть минимизирует квадрат ошибки »
K
при которой в случае подачи на его вход
казуального сигнала s(t)
)
K
сигнал x(t)=s(t)*g(t)
на его выходе наилучшим образом приближает
некоторый желаемый сигнал xж(t)
)
K,
то есть минимизирует квадрат ошибки »

Формирующий фильтр:
Фильтр с импульсной реакцией g0(t)=xж(t) называется формирующим фильтром для сигнала xж(t).
16Лек. Спектральное описание линейных непрерывных фильтров – определение комплексного коэффициента передачи фильтра (КЧХ) и его основное свойство. Определение амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик фильтров. Спектральные характеристики сигнала на выходе фильтра (комплексный и амплитудный спектры, спектральная плотность энергии).
Определение – Комплексный коэффициент передачи фильтра (КЧХ):
Комплексным коэффициентом передачи линейного непрерывного фильтра называется прямое преобразование Фурье F(∙) от ее импульсной характеристики
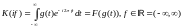
КЧХ полностью описывает поведение фильтра в частотной области.
Основное свойство КЧХ:
Пусть на входе линейного фильтра действует сигнал s(t) с комплексныи спектром Ps(if), а на выходе наблюдается сигнал x(t) со спектром Px(if), тогда КЧХ фильтра может быть вычислена по формуле

Амплитудно-частотной
характеристикой линейного фильтра
(АЧХ) называется вещественная функция
частоты, определяемая выражением
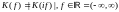
Фазо-частотной характеристикой (ФЧХ) линейного фильтра называется вещественная функция частоты, определяемая выражением

Спектральные характеристики:
Пусть на вход линейного фильтра с КЧХ K(if) действует сигнал s(t) с комплексным спектром Ps(if). Тогда… сигнала x(t) на выходе фильтра описываются выражениями:
Комплексный
спектр
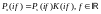
Амплитудный
спектр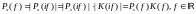
СПЭ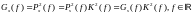
17Лек. Определение линейного неискажающего непрерывного фильтра, его КЧХ и ИХ. Основные параметры линейных фильтров – полоса частот фильтра, центральная частота, эффективная полоса пропускания, ширина полосы пропускания «на уровне 0,7».
Линейный
фильтр является неискажающим,
если при прохождении через него любого
сигнала s(t)
он сохраняет свою форму,
то есть выходной сигнал фильтра
 может отличаться от входного только
постоянным масштабным множителем
может отличаться от входного только
постоянным масштабным множителем
 и задержкой
и задержкой
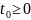 .
.
Комплексный
коэффициент
передачи (КЧХ) неискажающего фильтра:
 Из
уравнения следует, что
Из
уравнения следует, что
АЧХ
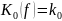 постоянна
на всех частотах
постоянна
на всех частотахФЧХ
 линейна
(вносимый фазовый сдвиг пропорционален
частоте).
линейна
(вносимый фазовый сдвиг пропорционален
частоте).
Если
мы примем выход фильтра
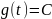 как некоторый сигнал с конечной энергией
как некоторый сигнал с конечной энергией
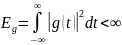 ,
то его физические характеристики
(амплитудный спектр, фазовый спектр,
СПЭ) мы можем
рассчитать подобно характеристикам
сигнала, как мы делали ранее (по смыслу
они совпадут с КЧХ, АЧХ, ФЧХ, квадратом
АЧХ).
,
то его физические характеристики
(амплитудный спектр, фазовый спектр,
СПЭ) мы можем
рассчитать подобно характеристикам
сигнала, как мы делали ранее (по смыслу
они совпадут с КЧХ, АЧХ, ФЧХ, квадратом
АЧХ).
Полоса частот:
КЧХ
фильтра сосредоточена в полосе частот
 ,
если уровень подавления
,
если уровень подавления
 излучения по мощности за пределами этой
полосы не превышает заданного:
излучения по мощности за пределами этой
полосы не превышает заданного:

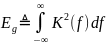
Верхняя
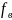 и нижняя
и нижняя
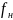 границы частотного диапазона определяются
из критерия
границы частотного диапазона определяются
из критерия

Центральная
частота
 на интервале
на интервале
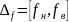 является центром
тяжести кривой
является центром
тяжести кривой
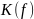 АЧХ на этом
интервале.
АЧХ на этом
интервале.
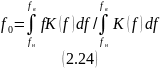
Эффективная ширина пропускания:
Пусть АЧХ фильтра сосредоточена в диапазоне частот , тогда эффективной шириной пропускания фильтра называется величина
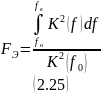
Пусть
фильтр описывается АЧХ с центральной
частотой f0
, тогда
шириной полосы пропускания фильтра «на
уровне 0,7» называется величина
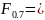 такие,
что выполняется равенство
такие,
что выполняется равенство

