
- •3Лек. Понятия свертки и скалярного произведения двух непрерывных сигналов, норма сигнала и взаимная ортогональность сигналов. Спектр свертки, классическое и обобщенное равенства Парсеваля.
- •5Лек. Спектральная классификация непрерывных вещественных сигналов: нч сигнал, пч, шпч, упч –сигналы, вч-сигнал, чо-сигнал. Ответ пояснить соответствующими графиками спектров сигналов.
- •9Лек. Центрированный прямоугольный импульс единичной амплитуды, длительности т, его комплексный спектр, спектральная плотность энергии и корреляционная функция. Изобразить их графики.
- •18Лек. Спектральная классификация линейных фильтров – понятия фнч, фпч, фвч, упч, шпч, чо-фильтр, рч-фильтр. Ответ пояснить соответствующими графиками ачх фильтров.
Оглавление
1 Лек. Спектральное описание непрерывных сигналов в частотной области определение энергии сигнала, комплексного, амплитудного и фазового спектров, двухсторонней и односторонней спектральной плотности энергии (СПЭ и ОСПЭ). Ответ пояснить соответствующими графиками спектров сигналов.
Аналоговый
(непрерывный)
сигнал
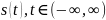 – вещественная или комплексная
детерминированная функция, заданная
на вещественной оси времени, а его
энергия конечна.
– вещественная или комплексная
детерминированная функция, заданная
на вещественной оси времени, а его
энергия конечна.
Энергия аналогового сигнала (Всегда конечна)
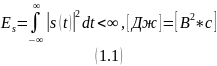
Если нужно подчеркнуть, что сигнал:
Вещественный:
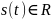
Комплексный:
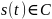
Комплексный
спектр
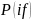 (КЧХ) – есть комплексное непрерывное
прямое преобразование Фурье (НПФ)
(КЧХ) – есть комплексное непрерывное
прямое преобразование Фурье (НПФ)
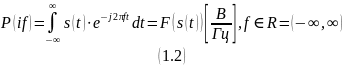
Зная
спектр сигнала, можно его однозначно
восстановить
с помощью обратного
преобразования Фурье (ОНПФ)
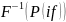
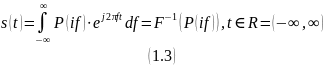
Амплитудный спектр (АЧХ) – неотрицательная вещественная функция частоты
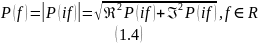
Фазовый спектр (ФЧХ) – вещественная функция частоты
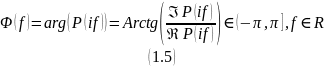
Спектральная плотность энергии – неотрицательная вещественная функция частоты
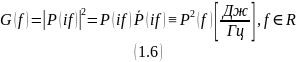
Если
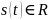 ,
то АЧХ и СПЭ всегда четны и неотрицательны:
,
то АЧХ и СПЭ всегда четны и неотрицательны:
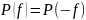 – АЧХ
– АЧХ
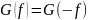 – СПЭ
– СПЭ
Односторонняя СПЭ
Исключая
все отрицательные частоты, мы можем
удвоить СПЭ при
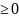 (исходя из четности СПЭ выше).
(исходя из четности СПЭ выше).
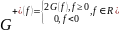
Одностороння СПЭ несет в себе ту же информацию, так как от двусторонней отличается только удвоенным масштабом вдоль вертикальной оси координат.
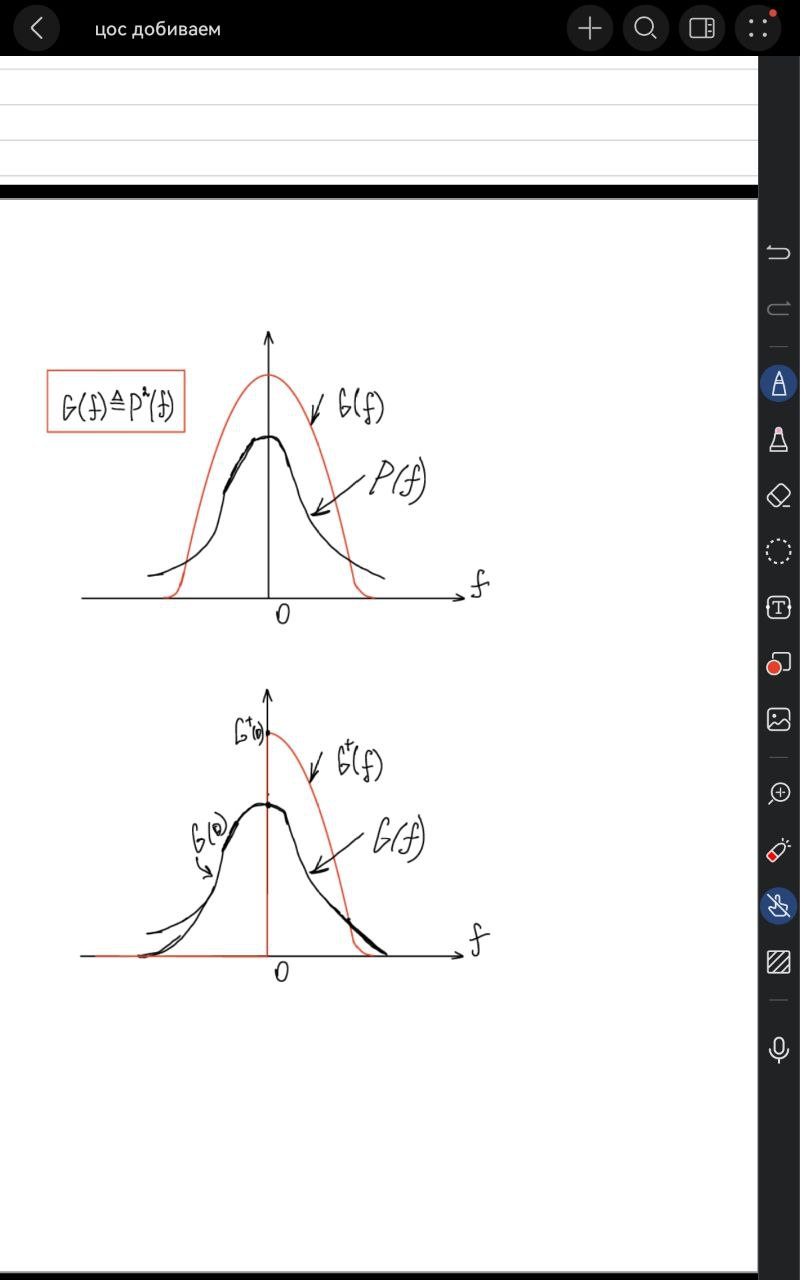
Спектральные характеристики вещественного НЧ сигнала.
2Лек. Свойства комплексного спектра непрерывного сигнала: линейность, сдвиг по времени, сдвиг по частоте (для комплексного и вещественного сигналов), сопряженная симметрия (или четность). Ответ пояснить соответствующими графиками спектров сигналов.
Свойство – линейность:
Если
сигнал s(t)=as1(t)
+ bs2(t),
a,
b,
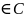 является линейной комбинацией двух
других сигналов s1(t)
и s2(t),
то его комплексный спектр Ps(if)
равен аналогичной линейной
комбинации комплексных спектров
этих сигналов, то есть
является линейной комбинацией двух
других сигналов s1(t)
и s2(t),
то его комплексный спектр Ps(if)
равен аналогичной линейной
комбинации комплексных спектров
этих сигналов, то есть
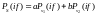
Свойство – сдвиг по времени:
Пусть
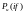 – комплексный спектр сигнала
– комплексный спектр сигнала
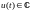 ,
тогда спектр смещенного во времени
сигнала
,
тогда спектр смещенного во времени
сигнала
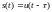 равен
равен
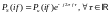
Свойство – сдвиг по частоте комплексного сигнала:
Пусть
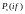 – комплексный спектр сигнала
– комплексный спектр сигнала
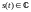 ,
тогда смещенный по частоте сигнал
описывается выражением
,
тогда смещенный по частоте сигнал
описывается выражением
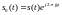 и справедливо
и справедливо
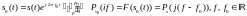
Свойство – сдвиг по частоте, сохраняющий вещественность сигнала:
Пусть
– спектр вещественного сигнала
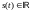 ,
тогда сдвинутый по частоте сигнал
описывается выражением
,
тогда сдвинутый по частоте сигнал
описывается выражением
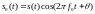 и
справедливо
и
справедливо
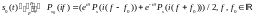
Где
левая и правая часть выражения связаны
прямым
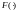 и
обратным
и
обратным
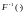 непрерывным
преобразованием Фурье, соответственно.
непрерывным
преобразованием Фурье, соответственно.
Свойство – спектр вещественного сигнала:
Если
– произвольный вещественный сигнал,
то его комплексный спектр обладает
свойством сопряженной
симметрии,
то есть
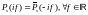
А
при четности сигнала его спектр становится
вещественным
и четным,
то есть
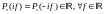
3Лек. Понятия свертки и скалярного произведения двух непрерывных сигналов, норма сигнала и взаимная ортогональность сигналов. Спектр свертки, классическое и обобщенное равенства Парсеваля.
Скалярное произведение сигналов
Пусть
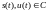 -
непрерывные детерминированные сигналы
с конечной энергией Еs,
Еu
< ∞, тогда их скалярным
произведением
называется
величина
-
непрерывные детерминированные сигналы
с конечной энергией Еs,
Еu
< ∞, тогда их скалярным
произведением
называется
величина
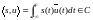 (1.48a)
(1.48a)
Которая
в случае вещественных сигналов
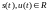 будет вещественной, т.е.
будет вещественной, т.е.
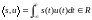 (1.48б)
(1.48б)
Нормы сигналов
Нормой
непрерывного сигнала
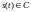 называется
величина
называется
величина
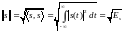 (1.50)
(1.50)
Очевидно,
норма
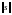 всегда неотрицательна и по смыслу
совпадает со среднеквадратическим
значением сигнала.
всегда неотрицательна и по смыслу
совпадает со среднеквадратическим
значением сигнала.
Ортогональность сигналов
Два непрерывных сигнала называются ортогональными, если их скалярное произведение равно нулю, т.е.

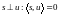 (1.52)
(1.52)
Если указанное свойство ортогональности выполняется попарно для нескольких сигналов, то они называются взаимно ортогональными.
Свертка двух сигналов
Свёрткой (s*u)(t)=s(t)*u(t) двух непрерывных сигналов называется сигнал х(t), определяемый формулой
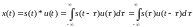 (1.17)
(1.17)
Спектр свёртки
Комплексный спектр свёртки x(t)=s(t)*u(t) двух непрерывных сигналов равен произведению их спектров, т.е.
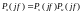 (1.18)
(1.18)
Классическое равенство Парсеваля
Энергией непрерывного сигнала , может быть вычислена по его спектральной характеристике Ps(f) или Gs(f) на основе классического равенства Парсеваля
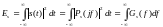 (1.19)
(1.19)
В
частности, для вещественного сигнала
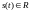 с односторонней СПЭ равенство Парсеваля
может быть записано в виде
с односторонней СПЭ равенство Парсеваля
может быть записано в виде
 (1.20)
(1.20)
Обобщенное равенство Парсеваля
Скалярное
произведение сигналов
может быть вычислено через их комплексные
спектры
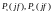 в частной области с использованием
обобщенного равенства Парсеваля
в частной области с использованием
обобщенного равенства Парсеваля
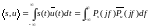
Нетрудно убедиться, что при s(t)=u(t) обобщенное равенство Парсеваля переходит в классическое (1.19)
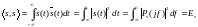
4Лек. Основные числовые характеристики спектра непрерывного сигнала – определение полосы частот сигнала f, ширины полосы частот F , центральной частоты f0,f00, эффективной ширины спектра Fэ, ширины спектра «на уровне 0,7» F0,7, физическая и геометрическая интерпретация для Fэ. Ответ пояснить соответствующими графиками спектров сигналов.
Определение – полоса частот и ее ширина:
Полоса
частот
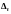 и ширина
полосы частот
F
вещественного сигнала
и ширина
полосы частот
F
вещественного сигнала
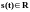 определяются следующими выражениями:
определяются следующими выражениями:
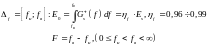 (1.21)
(1.21)
Откуда
следует, что основная доля энергии
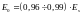 cигнала
s(t)
сосредоточена в частотном диапазоне
cигнала
s(t)
сосредоточена в частотном диапазоне
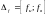 шириной
F.
шириной
F.
Определение – центральная частота амплитудного спектра f0:
f0>0
– центральная
частота амплитудного спектра
вещественного сигнала s(t)
на интервале
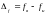 ,
если она является центом
тяжести кривой
Ps(t)
АЧХ сигнала на этом интервале, то есть
,
если она является центом
тяжести кривой
Ps(t)
АЧХ сигнала на этом интервале, то есть
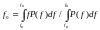
Определение – центральная частоты энергетического спектра f00:
Центральной частотой f00>0 энергетического спектра вещественного сигнала s(t) на интервале называется:
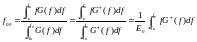 (1.24)
(1.24)
где G+ - односторонняя СПЭ (1.9) и E0 - энергия аналогового сигнала (1.2)
(!!)Центральные частоты зачастую оказываются близкими к друг другу или совпадают т.е f0≈ f00
(1.9) Эффективная ширина спектра
Эффективная ширина спектра вещественного сигнала, сосредоточенного в полосе частот определена формулой (1.25), где f00 - центральная частота
СПЭ (1.24).
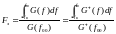 (1.25)
(1.25)
Физическая интерпретация:
Эффективная ширина спектра определяет частотный сдвиг, при котором два сигнала со сдвинутыми энергетическими спектрами G(f) и G(f-Fэ) при наложении друг на друга могут обнаружены и разделены по частоте, например, с помощью двух идеальных полосовых фильтров (ИПФ).

Геометрическая интерпретация:
Площадь
под кривой СПЭ
G+(f)
в полосе частот
равна
площади треугольника,
стороны которого равны G+(f)
и F,
то есть
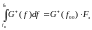
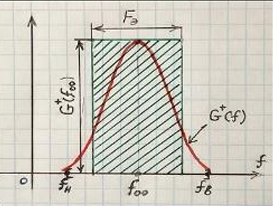
(1.10) Ширина энергетического спектра на уровне 0,5 и 0,7 амплитудного спектра
Пусть G(f), P(f) - СПЭ и АЧХ вещественного сигнала s(t), тогда ширина энергетического спектра:
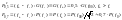 (1.27-1.28)
(1.27-1.28)
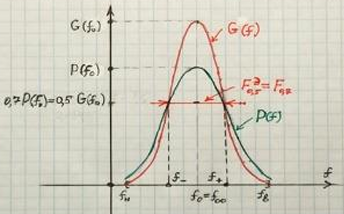
(!!) Обозначения и способы вычисления разные, но F0,5≡F0,
