
4 курс / 5 Дист. м. модели сетевого планирования
.pdfСЕТЕВЫЕ И ГРАФОВЫЕ МОДЕЛИ В ПЛАНИРОВАНИИ И УПРАВЛЕНИИ
1 Модели сетевого планирования
Эффективная реализация проекта, связанного с выполнением комплекса работ и протеканием параллельных процессов, представляет собой сложную и, как правило, противоречивую задачу. Оценка различных параметров функционирования системы (временных, ресурсных,
стоимостных и т.п.), осуществляемая в рамках решения этой задачи может производиться различными методами. Среди существующих методов в задачах рационального планирования комплекса взаимосвязанных работ большое значение имеет метод сетевого планирования.
Сетевое планирование – методы управления расписанием проекта,
которые основываются на использовании математического аппарата теории графов и системного подхода для отображения и алгоритмизации комплексов взаимосвязанных работ, действий и процессов для достижения поставленной цели.
Сетевое планирование позволяет определить, во-первых, какие работы или операции из числа многих, составляющих проект, являются
"критическими" по своему влиянию на общую календарную продолжительность проекта и, во-вторых, каким образом построить наилучший план проведения всех работ по данному проекту с тем, чтобы выдержать заданные сроки при минимальных затратах. В-третьих, сетевое планирование позволяет увязать выполнение различных работ и процессов во времени, получив модель прогноза общей продолжительности реализации всего проекта.
Основная цель сетевого планирования – сокращение до минимума продолжительности проекта.
Задача сетевого планирования состоит в том, чтобы графически,
наглядно и системно отобразить, и оптимизировать последовательность и взаимозависимость работ, действий или мероприятий, обеспечивающих своевременное и планомерное достижение конечной цели. Для отображения и алгоритмизации тех или иных действий или ситуаций используются математические модели, которые принято называть сетевыми моделями,
простейшие из них – сетевые графики. С помощью сетевой модели руководитель работ или операции имеет возможность системно и масштабно представлять весь ход работ или оперативных мероприятий, управлять процессом их осуществления, а также маневрировать ресурсами.
Принято разделять сетевое планирование на следующие методы:
1)Детерминированные сетевые методы
–диаграмма Гантта;
–метод критического пути;
2)Вероятностные сетевые методы
–неальтернативные (метод статистических испытаний (метод Монте-Карло), метод оценки и пересмотра планов (PERT));
–альтернативные (метод графической оценки и анализа (GERT).
2 Сетевой график
В основе сетевого планирования и управления лежит построение сетевых моделей (сетевых графиков, PERT диаграмм и т.п.). При этом под термином «сеть» понимается полный комплекс работ и событий проекта с установленными между ними зависимостями.
Обычно комплекс взаимосвязанных работ проекта состоит из ряда элементарных работ, которые взаимосвязаны таким образом, что выполнение некоторых из них не может быть начато раньше, чем закончатся другие работы или не будут выполнены определѐнные условия. Как правило,
количество таких звеньев работ большое, они сложным образом
взаимосвязаны, требуют большого числа разнообразных ресурсов и различного времени их исполнения.
Современное сетевое планирование начинается с разбиения проекта на отдельные работы (операции) и установления их взаимосвязей. Далее определяются продолжительности этих отдельных работ (операций), и
строится сетевая модель (график).
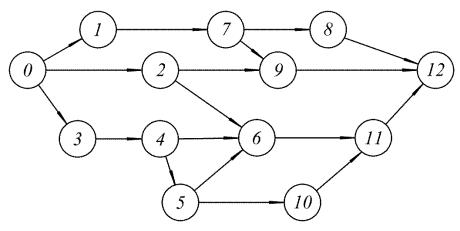
Сетевая модель – это графическое представление плана выполнения проекта. Сетевую модель, как правило, представляют графически в виде сетевого графика – «ориентированного графа» (см. рисунок 1), состоящего из стрелок (работ) и узлов (событий), которые отражают логическую взаимосвязь всех работ.
Рисунок 1 – Сетевой график
Построение сетевой модели позволяет проанализировать все операции и внести улучшения в структуру проекта до начала его реализации. Она позволяет найти минимальные сроки завершения проекта и отдельных работ,
а также определить множество критических работ, увеличение продолжительности выполнения любой из которых приводит к увеличению времени выполнения всего проекта. При построении сетевой модели, как правило, оперируют тремя основными понятиями:
1)работа (отдельная стрелка или ребро графа);
2)событие (отдельный кружок или узел графа);
3) путь (любая непрерывная последовательность работ и событий).
Работа – это процесс, приводящий к достижению намеченного результата. Каждая работа на сетевом графике объединяет два события
(начальное и конечное), поэтому обозначается двумя индексами этих событий. Работы делятся на три функциональных вида (рисунок 2):
1)Действительная работа – технологический процесс, требующий затрат времени, трудовых или материальных ресурсов. Обозначается сплошной стрелкой, длина которой может быть не связана с продолжительностью работы (если график выполнен не в масштабе времени). Как правило, у стрелки указываются продолжительность и наименование работы. Под стрелкой при необходимости могут указываться дополнительные сведения (необходимые ресурсы, стоимость, физический объем работ, исполнитель работ и т. д.);
2)Ожидание – процесс, требующий только затрат времени и не потребляющий никаких материальных ресурсов. В сущности, является технологическим или организационным перерывом между работами,
непосредственно выполняемыми друг за другом (например, затвердевание и набор бетоном прочности). Ожидание изображается так же, как, и
действительная работа, сплошной стрелкой с указанием продолжительности
инаименованием ожидания;
3)Фиктивная работа – процесс, не требующий ни времени, ни ресурсов, вводится для отражения технологической и организационной взаимосвязи работ. Отражает только логическую зависимость между функциональными операциями, представленными действительными работами или ожиданиями, показывает, что начало одной работы обусловлено либо окончанием другой работы, либо внешними обстоятельствами. Продолжительность фиктивной работы принимается равной нулю и изображают ее пунктирной стрелкой.
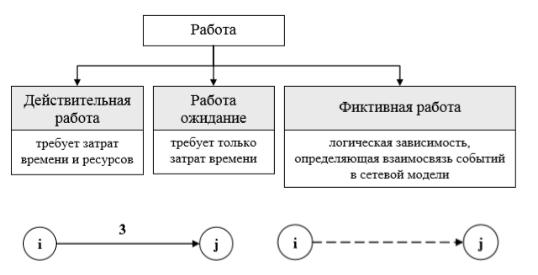
Рисунок 2 – Виды работ
Событие – это результат выполнения всех входящих в него работ.
События устанавливают технологическую и организационную последовательность работ. Считается, что событие происходит мгновенно.
На сетевом графе события изображаются в виде кружков (вершин графа).
Всем событиям присваиваются порядковые номера. Ни одна выходящая из данного события работа не может начаться до окончания всех работ,
входящих в это событие.
События ограничивают рассматриваемую работу и по отношению к ней могут быть начальными и конечными. Начальное событие определяет начало работы и является конечным для предшествующих работ. Конечное событие определяет конец работы и является начальным для последующих работ. На сетевом графике выделяют также особые события (рис. 3):
исходное событие (не имеет предшествующих работ и с которого начинается выполнение проекта); завершающие событие (не имеет последующих работ и которым заканчивается выполнение проекта).
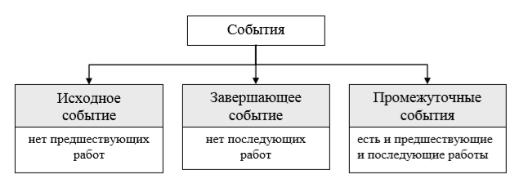
Рисунок 3 – Виды событий
Путь – это любая последовательность работ в сети, в которой конечное событие каждой работы совпадает с начальным событием последующей работы. Путь от исходного до завершающего события называется полным.
Путь от исходного до данного промежуточного события называется укороченным путем, предшествующим этому событию. Путь, соединяющий какие-либо два события, из которых ни одно не является исходным или завершающим, называется путем между этими событиями.
Продолжительность пути равна сумме продолжительностей составляющих работ. Полный путь, имеющий максимальную продолжительность, не имеющий резервов и включающий самые напряженные работы проекта,
называется критическим путем.
Работы, расположенные на критическом пути, называют критическими.
Все остальные работы являются некритическими (ненапряженными) и
обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.
При построении сетевых графиков необходимо соблюдать следующие правила:
1. Сеть изображается слева направо, и каждое событие с большим порядковым номером, как правило, изображается правее предыдущего.
Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим
номером.
2.Нумерация событий осуществляется по возрастанию – 0, 1, 2, 3, 4, …
3.Номер работы должен начинаться с меньшей цифры, чем еѐ конец
(т.е. 2-4, 1-6, но не 3-1).
3.На сетевом графике не должно быть событий и работ, имеющих одинаковые номера.
4.Два соседних события могут объединяться лишь одной работой.
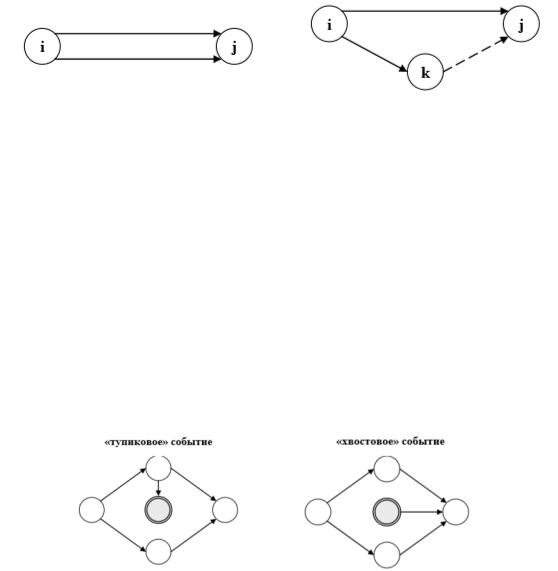
Нельзя две работы изображать параллельно. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис. 4).
Рисунок 4 – Правильное отображение двух параллельных работ на сетевом графике
5. Все события, кроме начального и завершающего, должны иметь предшествующую и последующую работу. На сетевом графике не должно быть «тупиков» и «хвостов», т.е. промежуточных событий, из которых не выходит или не входит ни одна работа (рисунок 5). Все работы должны быть связаны с начальным и конечным событием. «Тупики» на сетевом графике свидетельствуют о неточности построения сетевой модели или о логической ошибке, поскольку условия свершения события не будут обеспечены, либо указывают на то, что работа является лишней.
Рисунок 5 – Наличие «тупиков» и «хвостов» на сетевом графике
6. На сетевом графике сети не должно быть замкнутых «контуров»,
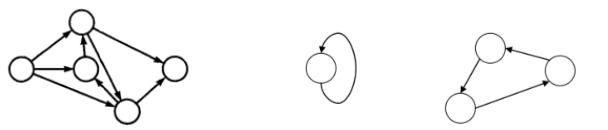
состоящих из взаимосвязанных работ, создающих замкнутую цепь или
«петель» (рисунок 6).
7.Если некоторые работы могут быть начаты после частичного выполнения работ, то предшествующую работу надо разбить на части и ввести дополнительные события.
8.Если для наступления события кроме работ, указанных на сетевом графике, нужны результаты от посторонних условий, то это изображается с помощью дополнительных надписей.
9.На сетевом графике следует избегать излишнего пересечения работ
(пересечений стрелок).
Рисунок 6 – Наличие замкнутых «контуров» и «петель» на сетевом графике
Процесс разработки сетевой модели разбивается на две стадии:
подготовка исходных данных и построение сетевого графика. На первой стадии необходимо выявить все взаимозависимости и установить продолжительности работ.
Начальным шагом первой стадии построения сетевого графика является установление последовательности выполнения работ и их взаимосвязей. Работы ij и jk называются взаимозависимыми, если одна из них может быть начата только после завершения другой. В противном случае они могут выполняться параллельно. Взаимосвязь между работами обычно представляют в виде матрицы связей (матрицы следования), обозначаемой
|| ij||. В этой матрице, состоящей из нулей или единиц, на пересечении строки j и столбца i ставится ij = 1, если работа j может начаться только после завершения работы i. В противном случае эти работы независимы, и ij = 0.
Вторым шагом первой стадии построения сетевого графика является
оценка продолжительности работ. Существуют два подхода к нахождению продолжительности ij-й работы (tij): детерминистический и вероятностный.
При первом подходе продолжительность tij представляют собой некоторую нормативную (постоянную) величину. При втором подходе продолжительность tij есть случайная величина, но при этом устанавливается закон и параметры еѐ распределения F(tij).
После нахождения всех времѐн tij и составления матрицы следования
|| ij|| переходят ко второй стадии – построению сетевого графика.
Используются две формы сетевого графика: полигональная и ортогональная.
В первом случае работы ij изображаются в виде безмасштабных стрелок,
длины которых не зависят от значения продолжительности работ tij, и эти стрелки могут представляться под любым углом к оси абсцисс. Во втором случае в нижней части графика вводится шкала времени t и работы изображаются в виде горизонтальных стрелок, длина которых пропорциональна времени tij. Для связи параллельных веток сетевого графика между собой используют фиктивные работы, изображаемые пунктирными линиями.
Полигональная форма обычно используется при поиске оптимального варианта сетевого графика, нахождении узких мест и резервов для их перераспределения. Ортогональная форма более удобна в качестве средства контроля за реализацией еѐ выполнения.
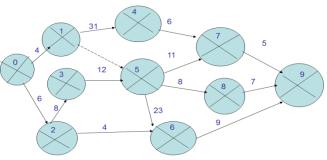
Пример построения простейшего сетевого графика с размеченными номерами событий и продолжительностями работ представлен на рисунке 7.
Рисунок 7 – Сетевой график полигональной формы
Следующей этапом сетевого планирования и управления является расчет и анализ параметров разработанного сетевого графика. К параметрам сетевого графика относятся: раннее и позднее начало работ, раннее и позднее окончание работ, длительность критического пути, резервы времени,
календарные даты и т.д. Основным временным параметром сетевого графика является продолжительность критического пути.
Ниже рассмотрен расчет параметров сетевого графика при фиксированных временах выполнения работ. Данный расчет относится к детерминированным методам сетевого планирования – методу критического пути. Однако, как указывалось выше, основы, заложенные в данном методе,
используются и в вероятностных методах сетевого планирования.
В ходе расчета и анализа параметров сетевого графика вычисляется критический путь и резервы времени выполнения работ, расположенных на других путях. При этом выполняются операции над событиями и работами.
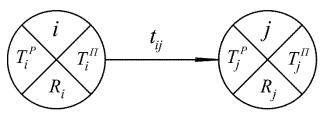
Любая ij-ая работа на сетевом графике ограничивается двумя событиями: событием i и событием j. Каждое i-ое, j-ое событие представляется в виде круга, разбитого на четыре сектора (рисунок 8), в
которые заносятся значения вектора характеристик события:
Si = (i, TiР, TiП, Ri),
где i – номер события на сетевом графике; TiР – наиболее ранний срок наступления i-го события (т.е. тот срок раньше которого по времени событие произойти не может); TiП – наиболее поздний срок наступления i-
го события (т.е. тот срок, позже которого событие не может наступить,
не нарушив продолжительности всего комплекса работ); Ri – резерв времени для наступления i-го события.
Рисунок 8 – Начальное и конечное события работы ij
