4 курс / 3 Дист. м. основы теории случайных процессов, ТМО

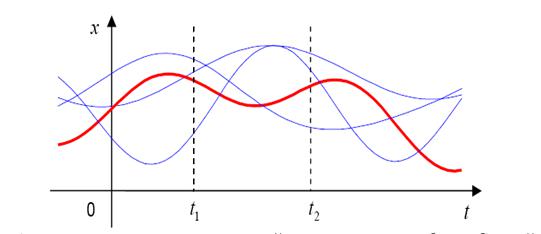
ОСНОВНЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ И ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ

1 Случайные процессы, потоки событий

Случайным процессом называют процесс, поведение которого в течение времени и результат заранее предсказать невозможно. Если речь идёт о системе, которая может находиться а различных состояниях, эти состояния также изменяются случайным образом и заранее их предсказать невозможно.

Теория случайных процессов – наука, изучающая закономерности случайных явлений и динамики их развития.

Случайный процесс - это случайная функция времени. Это означает, что наблюдатель «видит» только одну реализацию случайного процесса (она выделена на рисунке 1 красным цветом) из множества возможных функций (синие линии).

Рисунок 1 - Набор реализаций случайного процесса Полный набор всех возможных реализаций называют ансамблем.

Случайный процесс - это и есть ансамбль реализаций, а не функция в обычном понимании. Далее будем обозначать весь ансамбль (случайный процесс) через X(t). а отдельную реализацию - через х(t). Как правило, случайные процессы протекают в какой-либо системе. Например, заполнения

парка станции – случайный процесс, т.к. мы не можем предсказать заранее, в какое время будет занято то или иное количество путей. При этом в каждые новые сутки (каждую реализацию) ситуация будет разной и неповторимой.

Случайные процессы классифицируются по:

1)Характеру значений, принимаемых сечениями и реализациями:

–Случайный процесс X(t) называется процессом дискретным во времени, если система в которой он протекает, меняет свои состояния только в моменты времени t1, t2,…,tn, число которых конечно или счетно.

–Случайный процесс называется процессом с непрерывным временем, если переход их состояния в состояние может происходить в любой момент времени.

–Случайный процесс называется процессом с непрерывными состояниями, если значением случайного процесса является непрерывная случайная величина.

–Случайный процесс называется случайным процессом с дискретными состояниями, если значением случайного процесса является дискретная величина.

Как правило, рассматриваются случайные процессы с дискретными состояниями и непрерывным временем.

2)По характеру связи между сечениями:

–Процесс с независимыми сечениями. Процессы такого рода характеризуются тем, что любое конечное число сечений процесса представляет собой взаимно независимые случайные величины.Примеры процессов такого типа: величина «шума» (помех) в канале связи, измеряемая

вфиксированные моменты времени, достаточно удаленные друг от друга.

–Нормальные или гауссовские (гауссовы) процессы. Случайный процесс X(t) называют нормальным, или гауссовым, процессом, если любые его законы распределения являются нормальными.

–Процессы с независимыми приращениями. Случайный процесс X(t) называют процессом с независимыми приращениями, если значения разницы

между приращениями (изменениями X(t)) независимы друг от друга. Такие процессы широко применяются для моделирования потока заявок, поступающих на систему массового обслуживания (число отказов прибора, число автомашин перед светофором, подход поездов к станции и т. д.). Частным случаем процесса с независимыми приращениями является процесс Пуассона.

–Стационарные процессы. Случайный процесс X(t) называют стационарным, если его вероятностные закономерности не меняются во времени.

–Марковские процессы. К Марковским относятся процессы, для которых при фиксированном настоящем будущее не зависит от прошлого (процессы без последействия).

Важной составляющей случайных процессов являются потоки событий. Потоком событий называется некоторая последовательность однотипных событий, которые происходят в случайные моменты времени (например, прибытие поездов на станцию, звонки по телефону, посетители магазина, автомобили, проезжающие перекресток и т.д.). Они относятся к случайным процессамс дискретным состоянием и непрерывным временем.

Если события в потоке происходят поодиночке, а не группами из нескольких событий, то такой поток называется ординарным. Поток событий называется потоком без последствий, если для любых непересекающихся интервалов времени число событий в одном интервале никак не влияет на то, сколько и каким образом будут происходить события в другом интервале. Стационарным поток является такой поток, интенсивность которого не меняется с течением времени.

2 Марковские процессы и граф состояний

Ранее случайные величины рассматривались без привязки к какомулибо процессу. Процесс, как правило, может включать в себя далеко не одну случайную величину: например, анализируя работу парка приема сортировочной станции, можно заметить, что случайно будет и поступление составов на станцию, и время их технического осмотра и многие другие параметры, которые мы можем учесть. Конечная цель исследования любого случайного процесса – построение его математической модели. Как правило, подобная задача чрезвычайно сложна, однако в некоторых случаях такую модель всё-таки можно построить. Этот случай – когда исследуемый процесс является марковским.

Представим случайный процесс в виде некоторой модели: пусть

Однако, в каких-то случаях мы можем пренебречь случайностями, а в какихто нет. Вернемся к недавнему примеру, пусть система – парк приема сортировочной станции, тогда каждое её состояние будет характеризоваться количеством занятых и свободных путей. Как говорилось ранее, на систему воздействует ряд случайных факторов (случайных величин), следовательно, и состояния системы будут меняться случайным образом.

Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени 0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент 0 и не зависят от того, когда и как система пришла в это состояние.

состояниями и непрерывным временем. Процесс называется с дискретными состояниями, если все его возможные состояния 1, 2, 3 и т.д. можно заранее перечислить, а переход из одного состояния в другое переходит «скачком», т.е. мгновенно. Процесс называется процессом с непрерывным временем, если моменты переходов из одного состояния в другое распределены случайно и могут осуществиться в любой момент времени. Однако, раз процесс случайный, определить можно только вероятность, с которой процесс может перейти в то или иное состояние, т.е. вероятности состояний.

3 Уравнения Колмогорова для вероятностей состояний

Рассмотрим случайный процесс: техническое устройство состоит из двух узлов, каждый из которых может выйти из строя в случайный момент времени. Сразу же после этого начинается ремонт узла, время ремонта тоже длится какое-то случайное время. Перечислим возможные состояния системы: 0 - оба узла исправны; 1 - первый узел ремонтируется, второй исправен; 2 - второй узел ремонтируется, первый исправен; 3 – оба узла ремонтируются. Случайный процесс удобно представлять в виде графа состояний – геометрической схемой, демонстрирующей каким образом может меняться состояние системы (рис.2).

процессах являются простейшими. Подробнее о типах потоков будет рассказано в разделе теории массового обслуживания.

Таким образом, зная возможные состояния системы, а также интенсивности перехода из одного состояния в другое, остаётся определить вероятность того, что в произвольный момент времени система будет находиться в каком-либо из состояний . Вероятности состояний определяются с помощью уравнений Колмогорова. Для каждого состояния системы записывается своё уравнение: в его левой части стоит финальная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа – сумма произведений интенсивностей всех потоков, входящих в i-e состояние, на

Для получения точного результата необходимо одно из уравнений заменить так называемыми нормировочным условием. Если система может находиться только в 4-х известных состояний, то сумма+ +вероятностей+ = 1 нахождения в каждом из них равняется единице, т.е. 0 1 2 3 . Полученные вероятности можно интерпретировать как долю времени, когда система будет находится в определенном состоянии.

Если записать уравнения Колмогорова для графа, представленного на рисунке 5, можно получить формулы расчета вероятностей состояний

любого числа состояний (если рассматривается схема гибели и размножения)

эти вероятности могут быть определены2следующим образом:

0 = (1 + += 0 + + )−1

Схема гибели и размножения, как можно догадаться из названия, широко распространена в эволюционной биологии. С точки зрения транспорта её удобно использовать при решении задач теории массового обслуживания.

5 Теория массового обслуживания. Общие понятия.

Исследуя транспортные процессы, достаточно часто приходится сталкиваться с так называемыми системами массового обслуживания. Системы подобного рода достаточно широко распространены во всех областях жизнедеятельности: кассы в магазинах, очереди в гардероб или столовую, телефонные станции, железнодорожные станции, пункты погрузки-выгрузки и т.д. Исследованием процессов, протекающих в таких системах, занимается теория массового обслуживания. Целью теории массового обслуживания (далее ТМО) является определение основных характеристик, позволяющих оценить качество работы системы: длину очереди, время ожидания в очереди и др. Любая система массового обслуживания (далее СМО) состоит из какого-то числа обслуживающих единиц (аппаратов), называющихся «каналами» обслуживания. Каналы занимаются обслуживанием поступающих в СМО заявок (требований, событий). СМО бывают одноканальные (обслуживанием занимается один канал) и многоканальные (несколько заявок обслуживаются одновременно на параллельно работающих каналах). Обслуживание поступившей заявки продолжается какое-то время, после чего канал освобождается. Если до окончания обслуживания одной заявки в систему поступила другая, то образуется очередь. Очередь может быть ограниченной и неограниченной. В некоторых СМО очередь не предусмотрена, их называют «СМО с отказами». Как правило, на транспорте рассматриваются СМО с ожиданием, т.е. с наличием очередей. В общем виде структура любой СМО представлена на рисунке 5.