ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Кафедра безопасности информационных систем

ОТЧЁТ

по итоговой работе №4 на тему: «Рекурсия»

по дисциплине «Алгоритмы и структуры данных»

Выполнил: студент группы ИСТ-931, Гетманченко П.А.

«02» ноября 2020 г. ___________/П.А. Гетманченко /

Принял: к.ф.-м.н., доцент, Моисеев И. А.

«02» ноября 2020 г. __________/ И. А. Моисеев /

Основная часть

Цель работы: изучить понятия рекурсии, рекурсивные функции в программировании, приемы построения рекурсивной триады при решении задач, научиться применять рекурсивные методы в решении задач на языке С++.

Результаты выполнения работы

Задание 1:

Определить закономерность формирования членов последовательности. Найти n-ый член последовательности: 1, 1, 2, 3, 5, 8, 13, ... .

#include <iostream>

#include <clocale>

#include <Windows.h>

using namespace std;

int func(int n)

{

if (n <= 2)

return 1;

else

return func(n - 2) + func(n - 1);

}

int main()

{

setlocale(LC_ALL, "Russian");

int n;

cout << "Введите n: ";

cin >> n;

cout << n << "-й член последовательности: " << func(n) << endl;

system("Pause");

return 0;

}

Результаты:

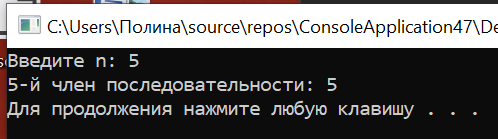
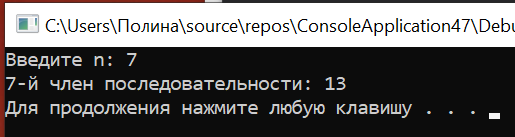
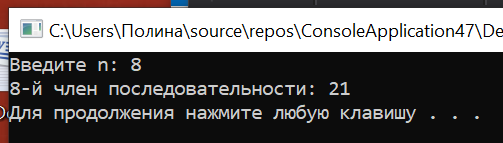
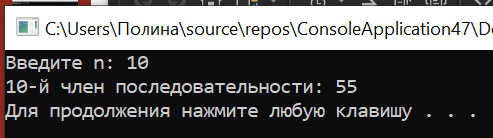
Закономерность:

1+1(1+1=2)+2(1+2=3)+3(2+3=5)+5(3+5=8)+8(5+8=13)+13(8+13=21)+21(13+21=34)+34(21+34=55)+55…

Задание 2:

Разработать алгоритм и программу вычисления числа сочетаний из n элементов по m:

Числа n и m вводятся с клавиатуры (n m). Решить задачу рекурсивно, выразив вычисление через

#include <iostream>

#include <clocale>

#include <Windows.h>

using namespace std;

int C(int n, int m)

{

if (m == n || m == 0)

return 1;

else

return C(n - 1, m - 1) + C(n - 1, m);

}

int main()

{

setlocale(LC_ALL, "Russian");

int m, n;

cout << "Вычисление числа сочетаний из n элементов по m" << endl;

cout << "n = "; cin >> n;

cout << "m = "; cin >> m;

cout << "Число сочетаний из " << n << " элементов по " << m << ": " << C(n, m) << endl;

system("Pause");

return 0;

}

Положительный результат:

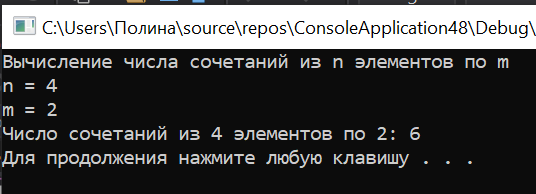
Отрицательный результат:

Так как нарушается условие (n меньше m, а ведь n должно быть больше или равно m), то программа ничего не выводит.

Задание 3:

Найти наибольший общий делитель двух натуральных чисел с помощью алгоритма Евклида, используя рекурсивный и не рекурсивный (итерационный) алгоритмы. Определить оценку сложности и провести сравнительный анализ двух алгоритмов.

#include <iostream>

#include <clocale>

#include <Windows.h>

using namespace std;

// рекурсивный алгорим Евклида

int EuclidRec(int a, int b)

{

if (a != 0 && b != 0)

{

if (a > b)

return EuclidRec(a % b, b);

else

return EuclidRec(a, b % a);

}

return a + b;

}

// итерационный алгорим Евклида

int EuclidIter(int a, int b)

{

while (a != 0 && b != 0)

{

if (a > b)

a %= b;

else

b %= a;

}

return a + b;

}

int main()

{

setlocale(LC_ALL, "Russian");

int a, b;

cout << "a = "; cin >> a;

cout << "b = "; cin >> b;

cout << "рекурсивный алгорим: " << EuclidRec(a, b) << endl;

cout << "итерационный алгорим: " << EuclidIter(a, b) << endl;

system("Pause");

return 0;

}

Результат:

Методы анализа сложности рекурсивных алгоритмов.

Сложность рекурсивного алгоритма сложно сопоставить с итерационным.

1. Итерационные алгоритмы

Анализ сложности – определение трудоёмкости конструкций “следование”, “ветвление”, “цикл” с использованием правил суммы и произведения.

2. Рекурсивные алгоритмы

Основные элементы:

1. Метод рекуррентных соотношений (только временная сложность).

2. Теоретико – графовый метод исследования дерева рекурсии.

Анализ сложности рекурсивных алгоритмов — одна из наиболее сложных и до конца нерешенных проблем метрической теории алгоритмов. Оценка сложности итерационных алгоритмов:

Отличие этих двух алгоритмов:

• рекурсивные алгоритмы, как правило, более затратные с точки зрения времени и памяти, нежели итерационные алгоритмы, решающие ту же задачу. При этом на сложность рекурсивного алгоритма большое влияние оказывает сама организация рекурсии.

Их можно использовать взаимозаменяемыми для решения различных проблем. В сущности, можно писать рекурсивные функции итеративно и наоборот.

Итерация может увеличить производительность программы. В то время как рекурсия может дать более интуитивный и элегантный результат.

Свойства:

Рекурсивная функция - это функция, которая частично определяется самим собой.

•Рекурсия использует структуру выбора;

•Бесконечная рекурсия возникает, если шаг рекурсии не уменьшает проблему таким образом, что сходится при некотором условии (базовый случай);

•Рекурсия завершается, когда базовый регистр распознается;

•Рекурсия обычно медленнее, чем итерация из-за накладных расходов на сохранение стека;

•Рекурсия использует больше памяти, чем итерация;

•Бесконечная рекурсия может привести к сбою системы;

•Рекурсия делает код меньше.

Итерационные функции – циклические повторения процесса.

•Итерация использует структуру повторения;

•Бесконечный цикл возникает с итерацией, если тест условия цикла никогда не становится ложным;

•Итерация завершается, когда условие цикла терпит неудачу;

•Итерация не использует стек, поэтому быстрее, чем рекурсия;

•Итерация потребляет меньше памяти;

•Бесконечный цикл использует многократные циклы CPU;

•Итерация делает код длиннее.

Задание 4:

Дано натуральное число, кратное 3. Получить сумму кубов цифр этого числа, затем сумму кубов получившегося числа и т.д. Проверьте на нескольких примерах, что любая такая последовательность чисел сходится к числу 153. Определить зависимость между вводимыми числами и количеством итераций.

21=>8+1=9=>729=>343+8+729=1080=1+512=513=>153

#include <iostream>

#include <clocale>

#include <Windows.h>

using namespace std;

void f(int x)

{

cout << x;

if (x != 153)

{

cout << "=";

int sum = 0, tmp;

while (x > 0)

{

tmp = pow(x % 10, 3);

cout << tmp;

sum += tmp;

x /= 10;

if (x > 0)

cout << "+";

else

cout << "=";

}

f(sum);

}

else

cout << endl;

}

int main()

{

setlocale(LC_ALL, "Russian");

int c;

cout << "Введите натуральное число, кратное 3: ";

cin >> c;

f(c);

system("Pause");

return 0;

}

Результат:

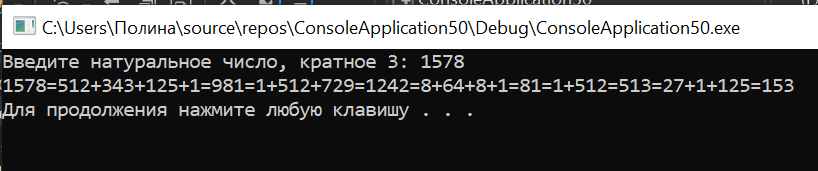
В первом случае 729 - это куб числа 9, которое было на прошлом шаге. И так уж получается, что число было одноразрядным, соответственно, в сумме всего одно слагаемое и как сумму кубов мы снова получаем 729.

Кубы идут в обратном порядке, т.к. числа берутся от младшего разряда к старшему, т.е. в методичке: 729=>7^3+2^3+9^3=343+8+729=1080 а в данном примере чуть наоборот: 729=729+8+343=1080 но суть та же.

Зависимость простая - чем больше интервал, и чем меньше значение требуемой точности, тем больше нужно итераций. Причём от точности сильнее зависит. 

Задание 5:

Исполнитель умеет выполнять два действия: "+1", "*2". Составить рекурсивную функцию для программы получения из числа 1 числа 100 за наименьшее количество операций. Определить количество операций.

#include <iostream>

#include <clocale>

#include <Windows.h>

using namespace std;

int f(int x)

{

cout << x;

if (x % 2 == 0)

{

x /= 2;

if (x != 0)

cout << " = 2*(";

}

else

{

x -= 1;

if (x != 0)

cout << " = 1+(";

}

if (x == 0)

return 0;

else

return 1 + f(x);

}

int main()

{

setlocale(LC_ALL, "Russian");

int x;

cout << "Введите число: ";

cin >> x;

int c = f(x);

for (int i = 0; i < c; i ++)

cout << ")";

cout << endl << "количество операций: " << c << endl;

system("Pause");

return 0;

}

Результат:

Выводы:

Рекурсия – это такой способ организации обработки данных, при котором программа вызывает сама себя непосредственно, либо с помощью других программ.

Рекурсивная функция – это функция, для которой существует алгоритм вычисления её значений по произвольному значению аргумента.

Были изучены приёмы построения рекурсивной триады при решении задач, научиться применять рекурсивные методы в решении задач на языке С++.

Содержание

Основная часть 2

Результаты выполнения работы 2

Выводы 12

Содержание 12

САНКТ-ПЕТЕРБУРГ 2020