МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Информационных систем и технологий

Кафедра Информационных управляющих систем

Направление: 09.03.02 Информационные системы и технологии

Профиль: Дизайн графических и пользовательских интерфейсов информационных систем

ОТЧЕТ

к лабораторной работе № 1:

«Аппроксимация функций»

по дисциплине «Нейросетевые технологиий»

Выполнил:

Студент группы ИСТ-931

Гетманченко П.А. «_25_»__марта__ 2022 г.

Принял:

преп. каф. ИУС

Капитоненко В.В. «_26_»__марта__ 2022 г.

Санкт-Петербург

2022 г

СОДЕРЖАНИЕ

ЦЕЛИ РАБОТЫ 3

ХОД РАБОТЫ 4

Задание №1 (вариант №2) 4

Листенинг 4

Задание №2 (вариант №2) 7

Листенинг 7

ВЫВОД 10

ЦЕЛИ РАБОТЫ

Цели работы (2 вариант):

- смоделировать заданную функцию на отрезке [0, 8] с использованием библиотеки neuralnet;

- подобрать структуру hidden и порог функции ошибки threshold для точной аппроксимации заданных последовательностей импульсов.

ХОД РАБОТЫ

Задание №1 (вариант №2)

Смоделировать функцию 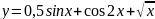на отрезке [0, 8] с использованием библиотеки neuralnet.

Листенинг

# Формирование данных learn для обучения (где set.seed – генератор псевдослучайных чисел, runif – показывает: сколько точек (чисел) на отрезке от 0 до 8, plot – график (pch – вид точки (квадратики, ромбики, но в данной ситуации – кружки), cex – размер кружка, col – цвет кружка), learn=data.frame(x,y) – обучение сети)

set.seed(9)

x <- runif(50,0,8)

y <- 0.5*sin(x)+cos(2*x)+sqrt(x)

plot (x, y, pch = 16, cex = 1.5, col = 'blue')

learn=data.frame(x,y)

# Загрузка библиотеки и обучение сети netcos (где загрузка библиотеки neuralnet, задаём формулу, hidden – количество нейронок и обучение)

library(neuralnet)

netcos <- neuralnet(y~x, hidden = 4, learn)

# Формирование тестовых данных и проверка сети netcos (где predict – вычисляет реакцию обученной сети netcos в переменной yp)

set.seed(6)

x <- runif(5000,0,8)

y <- 0

test=data.frame(x,y)

yp <- predict(netcos,test)

points(x, yp, col = 'green', pch = '.', cex = 1.5)

# Архитектура сети netcos

plot(netcos)

# Функции на выходах нейронов скрытого слоя

y1=1/(1 + exp(3.02803*x - 21.27729))

y2=1/(1 + exp(2.84433*x - 15.6538))

y3=1/(1 + exp(1.05947*x - 3.58056))

y4=1/(1 + exp(-3.06391*x + 7.48355))

# Графики функций на выходах нейронов скрытого слоя

set.seed(6)

x <- runif(5000,0,8)

plot(x,y4,col="red")

points(x,y1,col='grey')

points(x,y2,col='yellow')

points(x,y3,col='green')

#Функция и график на выходе сети netcos

y=y1*1.76509+y2*(-5.26569)+y3*8.47824+y4*5.46832-3.40245

plot(x,y)

Промежуточные графики показаны на рисунках 1-4:

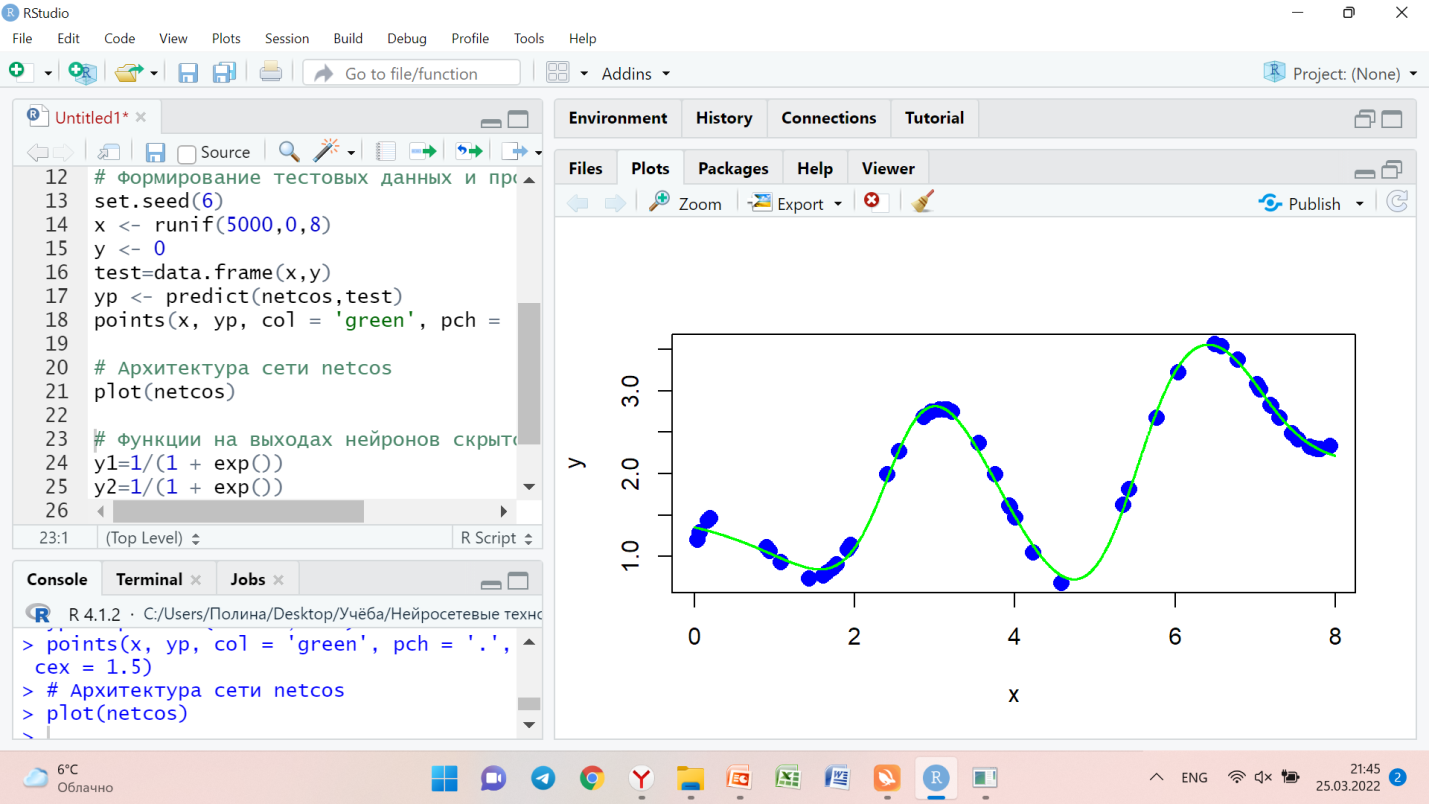
Рисунок 1 – график №1

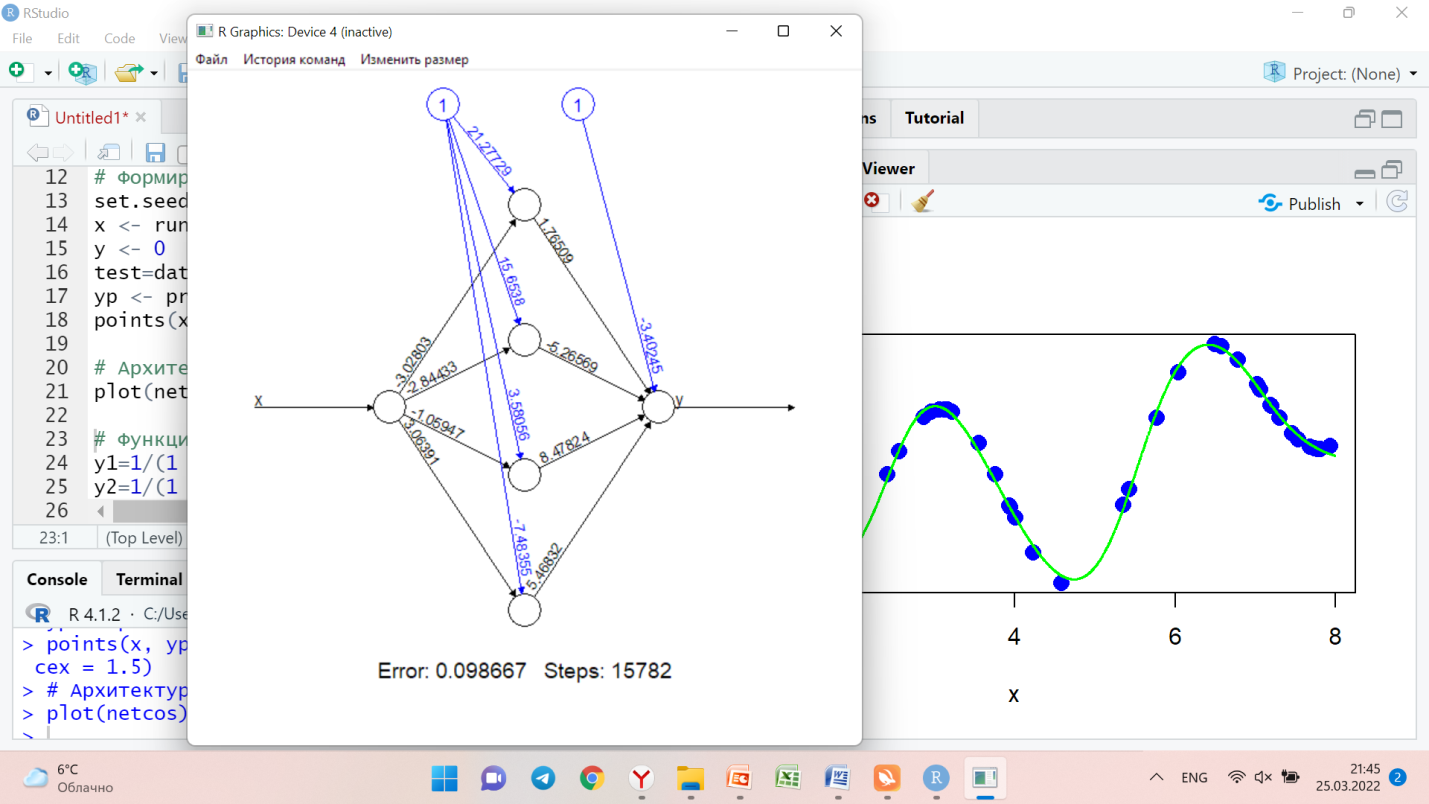
Рисунок 2 – график №2

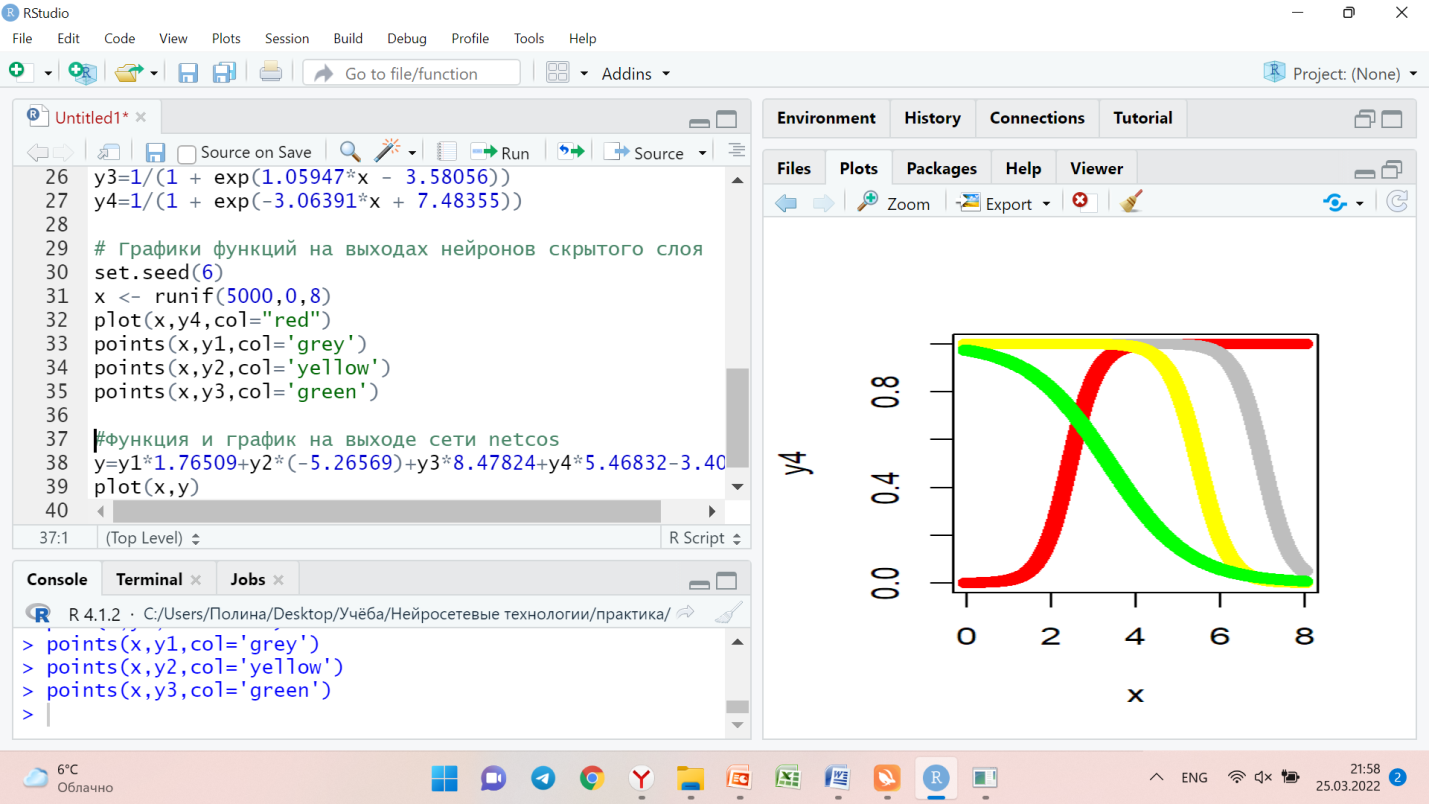
Рисунок 3 – график №3

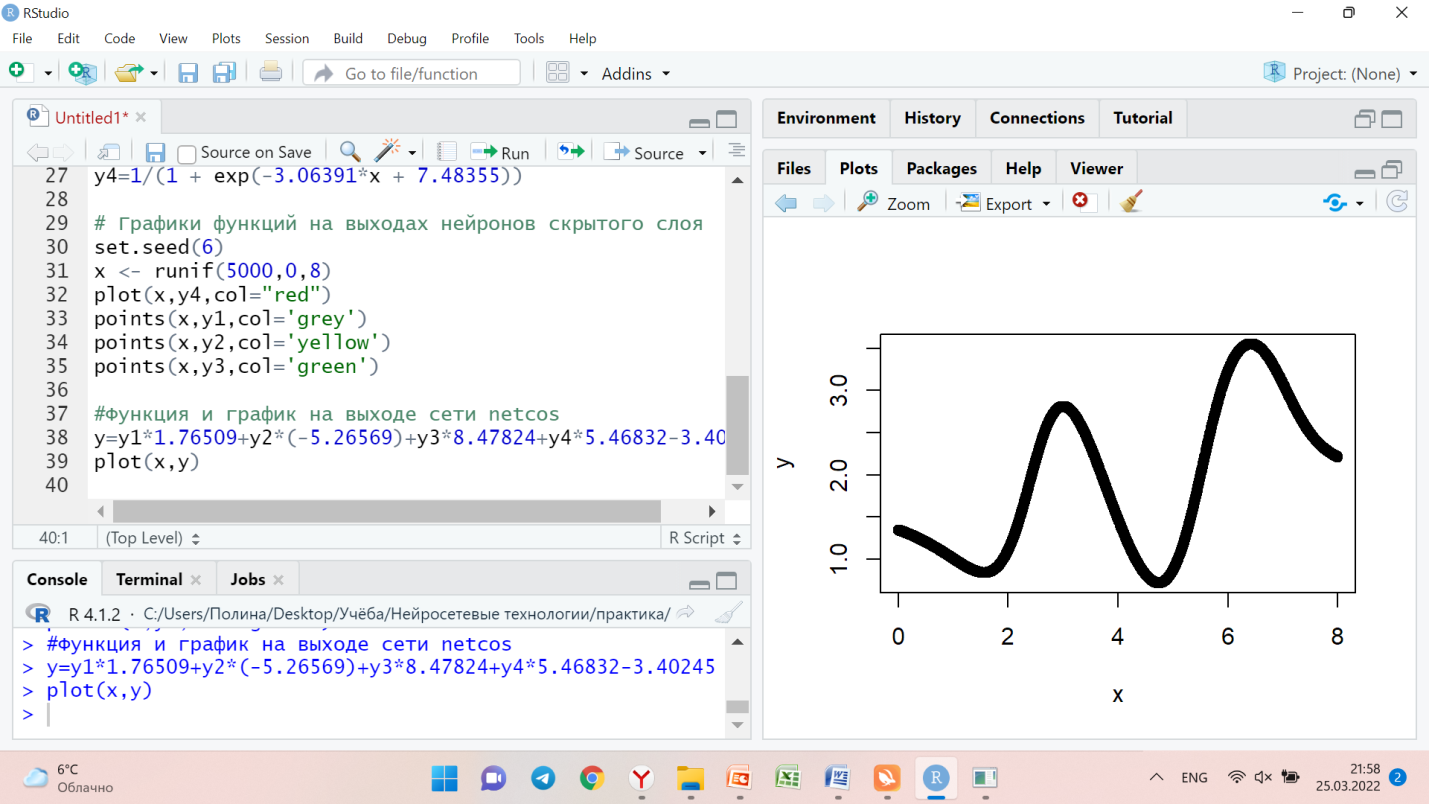
Рисунок 4 –график №4

Задание №2 (вариант №2)

Подобрать структуру hidden и порог функции ошибки threshold для точной аппроксимации заданных последовательностей импульсов.

Листенинг

# seq – генератор последовательности чисел, rep – итерационная функция

set.seed(9)

x <- runif(5000,-9.5,10)

x <- seq(from = -9.5, to = 10, by = 0.5)

y <- rep(c(1,1,1,1,1,0,0,0,0,0),4)

# для того, чтобы разместить 2 графика горизонтально – нужна библиотека - ggpubr

learn=data.frame(x,y)

library(neuralnet)

library(ggpubr)

# plot – график, а lines – функция, принимающая координаты, заданные различными способами, и соединяющая соответствующие точки с отрезками линий, threshold – порог функции ошибки

netcos <- neuralnet(y~x, hidden = c(10,10), threshold = 0.001, learn)

plot(netcos)

yp <- predict(netcos,learn)

plot(x, yp, type = 'l', col = 'yellow', lwd = 9)

lines(x,yp,col='black')

netcos <- neuralnet(y~x, hidden = c(25,20,10), threshold = 0.005, learn)

plot(netcos)

yp2 <- predict(netcos,learn)

plot(x, yp2, type = 'l', col = 'yellow', lwd = 9)

lines(x,yp2,col='black')

# paw – позволяет уместить два графика горизонтально

par(mfrow=c(1,2))

plot(x, yp, col='yellow', type = 'l', lwd = 9)

lines(x,yp2,col='black')

plot(x, yp2, horizontal=TRUE, col='yellow', type = 'l', lwd = 9)

lines(x,yp2,col='black')

Результат показан на рисунке 5:

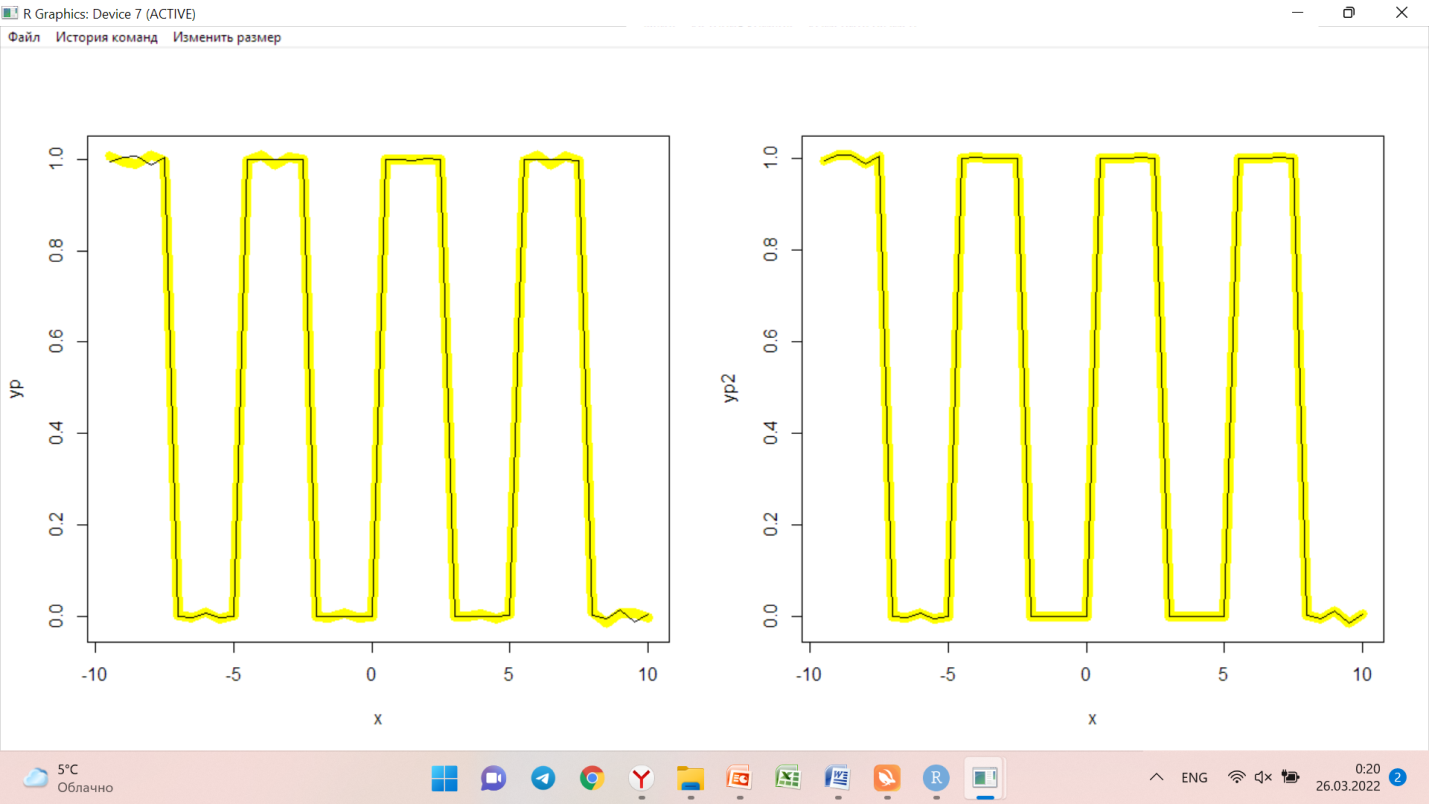
Рисунок 5 – результат задания №2

ВЫВОД

При выполнении лабораторной работы №1:

- смоделирована заданная функция на отрезке [0, 8] с использованием библиотеки neuralnet;

- подобрана структура hidden и порог функции ошибки threshold для точной аппроксимации заданных последовательностей импульсов.