ТММ. Курсач+

НИУ МИЭТ

Курсовая работа по технической механике микросистем

Вариант №26

Группа: ЭН-22

Студент: Ивакин Максим Александрович

Преподаватель: Угольников Сергей Викторович

Зеленоград 2024

А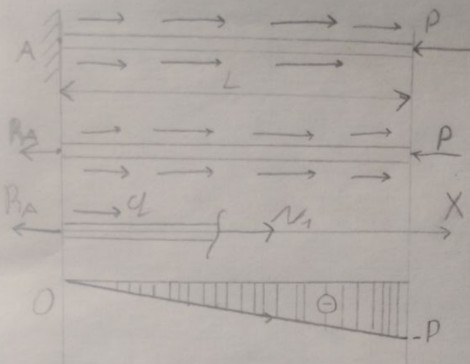 нализ внутренних силовых факторов

26.1

P=qL

У ч 1.

26.2

Уч. 1.

Уч. 2.

Уч. 3.

2 6.3

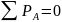
Уч. 1. ;

Уч. 2. ;

2 6.4

Уч.1

Уч. 2. ;

Уч. 3.

2 6.5

Уч.1 ;

Уч. 2. ;

Уч. 3.

2 5.6

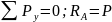
Уч.1

Уч. 2. ;

26.7

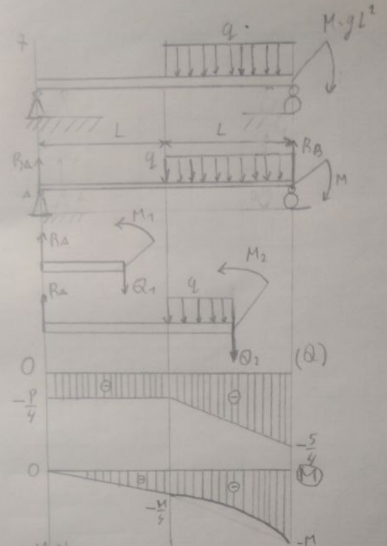
Уч.1

Уч. 2.

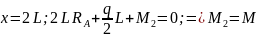
2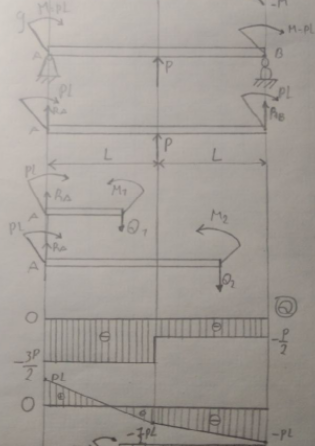 6.9

Уч.1

Уч. 2.

2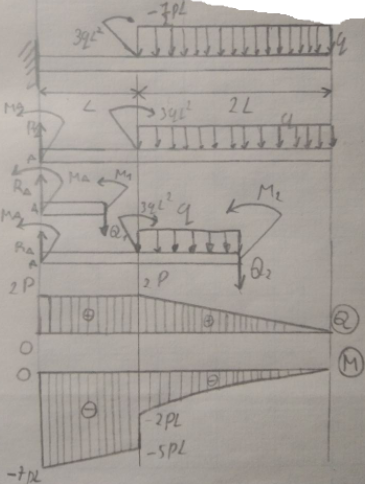 6.10

Уч.1

Уч. 2.

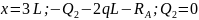
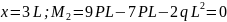
2 6.11

Уч.1

Уч. 2.

Уч. 3.

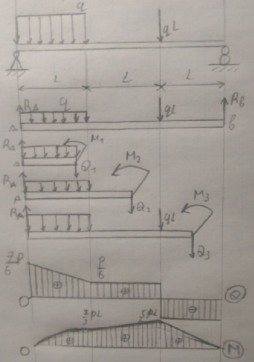2 6.12

Уч.1

Уч. 2.

Уч. 3.

Курсовая работа часть 2.

Расчет на прочность двуслойного соединения кристалл – кристаллодержатель.

Дано: h₁=0,46мм, a=10мм, b= 12мм. Число интерф. Колец n_x=50, h_z=72. Материал кристалла – кремний. E₁=1,7*10^5 Мпа, δ_в1=700Мпа, η₁=0,27.

Материал кристаллодержателя 42Н. E₂=1,5*10^5 Мпа, δ_в2=1200Мпа, η₂=0,29, h₂=0,23мм. Длина волны λ=0,65 мкм.

1. Радиус кривизны сборки в плоскости y_0x, y_0z

2. Положение нейтрального слоя относительно границы раздела

Минус означает, что граница раздела дальше от нейтрального слоя, чем от окружности радиуса , т.е нейтральный слой расположен в слое кристалла.

3. Координаты точек на свободных поверхностях и границе раздела

4. Момент инерции кристалла единичной ширины относительно нейтрального слоя.

5. Момент инерции кристаллодержателя единичной ширины относительно нейтрального слоя.

6. Изгибающий момент Изгибающий момент, действующий на пластину единичной ширины.

При

7. Нормальные силы, действующие в слоях.

Т.к

8. Распределение напряжений по толщине элементов сборки.

а) Напряжение кристалле на верхней свободной поверхности.

Б)Напряжение в кристалле на границе раздела с кристаллодержателем

В) Напряжение в кристаллодержателе на границе раздела с кристаллом:

г) Напряжение в кристаллодержателе на нижней свободной поверхности.

Рис. 8

Важно так же отметить, что:

9. Аналитика Эпюр напряжений по толщине сборки показывает, что вдоль осей x и z кристалл верхней(свободной) поверхности испытывает растяжение, а на границе раздела с КД сжатие. Кристаллодержатель на границе раздела с кристаллом испытывает растяжение, и на нижней(свободной) поверхности растяжение.

Максимальное напряжение в слое кристалла возникает на нижней поверхности раздела с кристаллодержателем вдоль осей x и z.

Максимальное напряжение в слое кристалла возникает на нижней поверхности раздела с кристаллодержателем вдоль осей x и z.

|

Допускаемое напряжение для материала кристалла ( Si )

[

Максимальное напряжение возникает на верхней поверхности(границе раздела с кристаллом)

Допускаемое напряжение для материала кристаллодержателя 42H:

[

Условие прочности выполняется, т.к:

Т.к обеспечивается прочность слоев кристалла с кристаллодержателем, то обеспечивается прочность всей сборки в целом.

Курсовая работа часть 3

Микроэлектронные пьезорезистивные датчики ускорения.

Расчет механических и метрологических характеристик.

Рис.1. Расчетная схема датчика: 1 – инерционная масса; 2 - демпфер; 3 - основание; 4 - тензометрический мост; 5 - ТКБ; 6 - поперечное сечение инерционной массы, C – центр тяжести инерционной массы; b, H, L - ширина, толщина и длина ТКБ соответственно; LR – расстояние от центра тяжести инерционной массы до тензомоста.

Дано:

L-2,1mm, b=2mm,H=0,1mm,L_R=1,65 mm, E=1,7*10^5МПа,K_П=(

U_m=0,54U_пит=0,54*9=4,86В. U_пит=9В. а=500(g) m=30мг ∆ν=0…1200Гц, ξ=0,05

1. Определить рабочую деформацию

2. Находим чувствительность датчика.

3. Коэффициент прочности ТКБ.

4. Частота собственных колебаний ТКБ.

5. Перемещение инерционной массы:

6. Определяем добротность датчика

7. Выходной сигнал описываем выражением:

,

Быстродействие

Рис.2. Переходная характеристика датчика

8. Динамическая чувствительность

Рис.3. Амплитудно-частотная характеристика датчика

При ν=1

9. 

10. Сдвиг фаз

=

Рис.4. Фазочастотная характеристика датчика

Курсовая работа часть 4

Расчет двухкоординатного микрозеркала на торсионных подвесах.

Вариант 13.

Дано: а₄=400мкм, а₅=360мкм, с₁=3мкм, с₂=3,5 , h₀=3мкм, d = 25 мкм,

ϴ­­⁰=5. Материал отражающего слоя Au, h_m=0,5мкм, ∆T=50⁰c, ρ_au=19 ,

E=0,8*10^5МПа, G=0,32*10^5, α=14*10^-6

Рис. 1

Si: ρ_si=2,33 , E_si=1,7*10^5МПа

G=0,68*10^5МПа

α_si=4,7*10^-6

а₃= а₄+20=420мкм

а₂= а₃+2d=420+50=470мкм

Масса зеркального элемента

Рис. 2

Момент инерции сечения торсиона:

Длина Торсиона при ϴ­­⁰=5:

Рис 3

Максимальное растягивающее напряжение в заделке торсионов для угла ϴ­­⁰=5

Коэффициент допустимой динамической перегрузки для угла отклонения ϴ­­⁰=5

Расчет рамы на торсионах

d=24мкм, a₁=670 мкм, a₂=470 мкм, a₃=420 мкм

Рис. 4

Допуск по напряжению в торсионе:

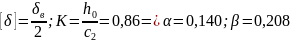
Крутящий момент на торсионе рамы

Длина Торсиона рамы при закручивании на ϴ­­⁰=5

Максимальное растягивающее напряжение при изгибе торсиона рамы от действия веса зеркала и рамы:

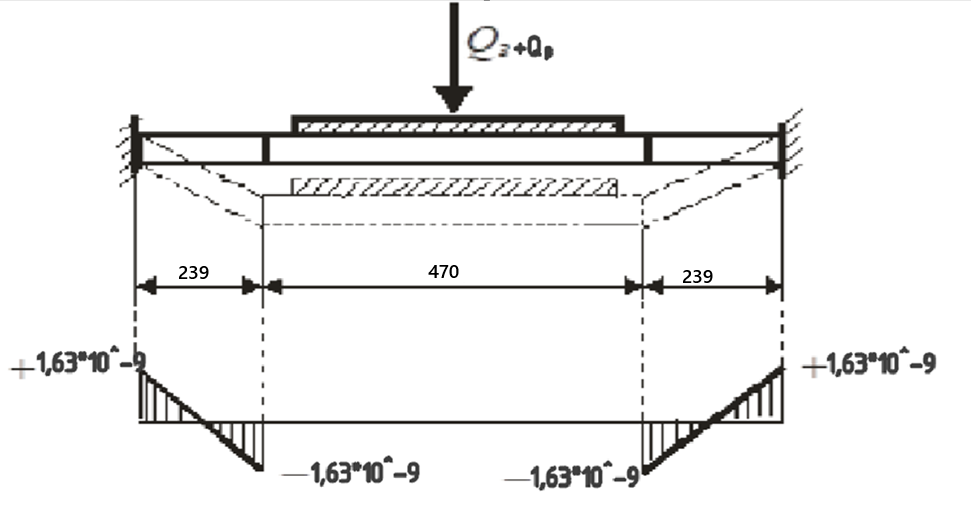
Рис. 5

Коэффициент допустимой динамической нагрузки

Расчет прогиба зеркального элемента в рабочем диапазоне температур

∆T=50⁰c, E_si=1,7*10^5Мпа, E=0,8*10^5Мпа, h₀=h₂=3мкм, h₁=h_au=0,5мкм.

Момент инерции

Рис.6

Момент инерции определяется:

Для расчета

Расчет резонансной частоты микрозеркала.

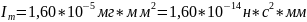
Резонансная циклическая частота зеркального элемента определяется по формуле:

= =1401Гц

=

Момент инерции рамы определяется разбиением рамы на определенные области, по которым проще считать общий момент инерции.

Рис. 7

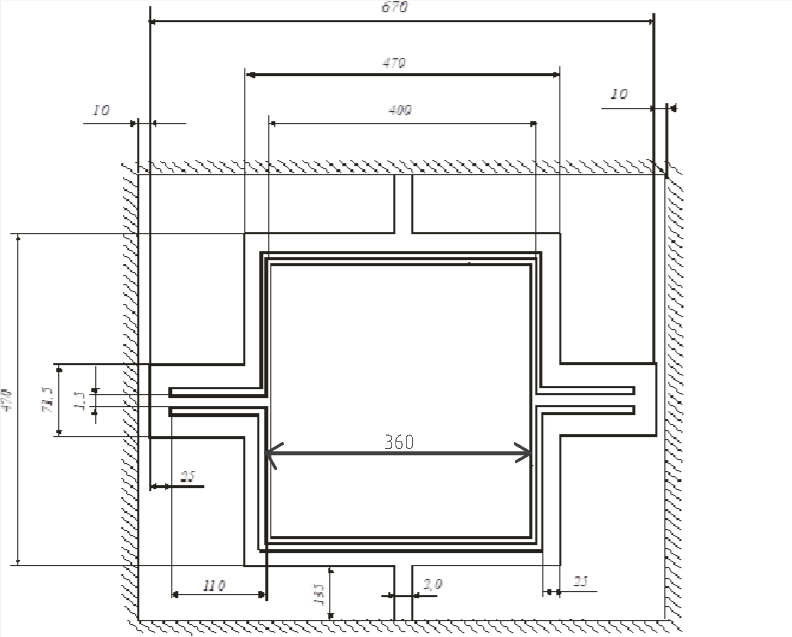
Рис. 8