
Вопросы к экзамену
.docВопросы по курсу “Дискретная математика”
Понятие и виды записи множества. Операции над множествами. Диаграммы Эйлера-Венна.
Определение множества – Множество – это количество предметов или чисел, обладающих общими свойствами.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2.
Выделяют три вида множеств: конечные - совокупности, имеющие максимальный и минимальный предел (например, отрезок); бесконечные - не являющиеся конечными (например, числовые); пустые (обозначаются Ø) – не имеющие элементов.
Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества.
Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В:
![]()
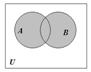
Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В:
![]()
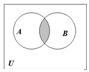
Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В:
![]()
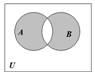
Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В:
![]()
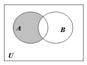
Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А:
![]()
Основные тождества алгебры множеств. Показать на диаграммах Эйлера-Венна выполнение дистрибутивности, закона де Моргана, закона поглощения.
Основные тождества алгебры множеств. Для любых множеств. A, B, C справедливы следующие тождества:
1. Коммутативность.
а) A u B = B u A (для объединения);
б) A л B= B л A (для пересечения).
2. Ассоциативность.
а) A u (B u C)= (A u C) u C (для объединения);
б) A л (B Ç C)= (A л B) л C (для пересечения).
3. Дистрибутивность.
а) A u (B л C)= (A u B) л (A u C) (для объединения относительно пересечения);
б) A л (B u C)= (A л B) u (A л B) u (A л C).






Понятие подмножества, мощности множества. Равносильные утверждения для подмножеств.
Прямое произведение множеств. Графическая иллюстрация. Примеры.
Отношение. Обратное отношение. Композиция отношений. Примеры.
Свойства отношений. Графическое представление отношений в декартовых координатах и графом.
Специальные бинарные отношения. Частично-упорядоченные множества. Диаграммы Хассе.
Основные понятия графа (ребра, вершины, степени вершин, инцидентность, смежность, типы графов). Примеры.
Матричное представление графа.
Путь, цепь, цикл в графе. Числовые характеристики графа. Примеры.
Связность, компоненты связности, матрица связности.
Алгоритм Терри поиска пути в связном графе.
Алгоритм фронта волны для нахождения минимального пути в графе..
Нагруженный граф. Алгоритм построения минимального остовного дерева графа. Пример.
Алгоритм построения остовного дерева графа. Пример.
Понятие высказывания. Определение логических связок. Таблицы истинности.
Равносильность формул логики высказываний. Основные и дополнительные равносильности.
Алгоритм приведения формулы логики высказываний к ДНФ и КНФ. Пример.
Условия и алгоритм приведения формулы логики высказываний к СДНФ и СКНФ.
Алгоритм представления булевой функции формулами в СДНФ и СКНФ. Пример.
Представление переключательных схем формулой логики высказываний. Пример.
Понятие предиката, кванторов, интерпретации. Примеры.
Правила для кванторов в логике предикатов.
