3.​ Минимальная связность. Для того, чтобы сохранить связность дерева, достаточно иметь n-1 ребро, где n - число вершин.

4.​ Единственность пути. Между любыми двумя вершинами в дереве существует ровно один путь.

5.​ Висячие вершины. В дереве всегда есть как минимум две висячие вершины (вершины с только одним ребром, соединяющим их с деревом).

6.​ Центр дерева. Если число вершин дерева нечетно, то в нём существует единственная центральная вершина. Если число вершин четно, то в дереве либо один центр (единственная центральная вершина), либо два центра (пара смежных центральных вершин).

7.​ Листья. Вершины дерева, имеющие степень 1, называются листьями.

44. Остовное дерево, остовной лес – определения. Код Прюфера. Восстановите дерево по данном коду Прюфера

Определение (остовное дерево)

Остовное дерево графа 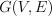– ациклический связный подграф (дерево) данного связного

неориентированного графа, в который входят все его вершины

Определение (остовной лес)

То же, что и остовное дерево, но не обязательно связное

Алгоритм (код Прюфера)

Код Прюфера – это способ взаимно однозначного кодирования помеченных деревьев с n

вершинами с помощью последовательности 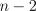целых чисел

На вход подается список ребер.

Выбирается лист дерева с наименьшим номером, затем он удаляется из дерева, и к коду Прюфера добавляется номер вершины, которая была связана с этим листом.

Эта процедура повторяется раза. В конце концов, в дереве останется только 2 вершины,

иалгоритм на этом завершается. Номера оставшихся двух вершин в код не записываются.

Пример

Дано дерево: