Закон Кулона
Закон Кулона — величина электрической силы между двумя точечными зарядами в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
= |
| 1|| 2| |
, где |
= 9 · 10 |
9 |
Н·м2 |
2 |
|
|
Кл2 |
Системы единиц
СИ и СГС (сантиметр грамм секунда) — в СГС отсутствуют некоторое постоянные, либо равны единице, такие как электрическая постоянная в законе Кулона. В целом СГС более предпочтительна если хочется вести теоретические исследования.
Электростатическое поле
Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами.
Принцип суперпозиции
Принцип суперпозиции — силы, создаваемые набором зарядов равны линейной сумме сил
→ →
= ∑ (не справедливо для сильного взаимодействия)
Допущение, согласно которому результирующий эффект нескольких независимых воздействий есть сумма эффектов, вызываемых каждым воздействием в отдельности.
Принцип суперпозиции описан в базовых знаниях, единственное что можно добавить так это
посмотреть как он работает на этом сайте: Закон Кулона • Физика, Электростатика • Фоксфорд Учебник
2. Потенциальные поля. Потенциал. Работа в электростатических полях. Связь между напряженностью и потенциалом. Теорема о циркуляции. Примеры вычисления распределения потенциала для сферической и цилиндрической форм симметрии.
Потенциальные поля
Поле называется потенциальным, если работа, совершаемая при перемещении тела по любому замкнутому контуру равна нулю. Силы электростатического взаимодействия в потенциальном поле – консервативные.
Электростатическое поле соответствует этим двум условиям, поэтому его можно считать потенциальным.
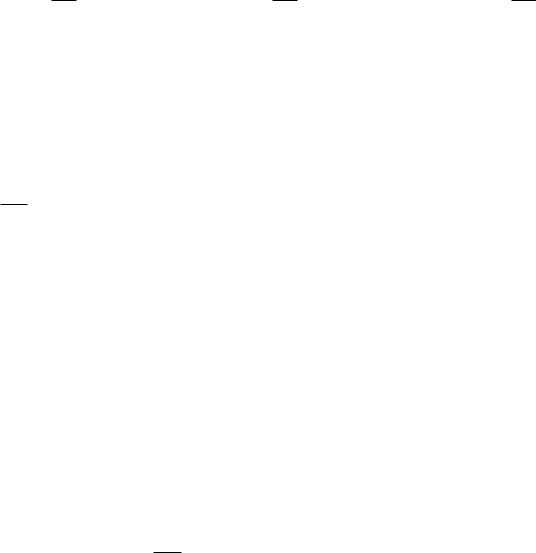
В общем виде: потенциальное векторное поле A — поле, которое можно представить в виде
градиента какого то скалярного поля O.
При этом поле O называется потенциалом векторного поля А.
Другими словами, векторное поле А является потенциальным если координаты какого нибудь вектора в этом поле, допустим вектора T, можно представить в виде частных производных скалярного поля O
= |
∂∂ |
|
|
|
= |
∂∂ |
|
|
|
= |
∂∂ |
|
Потенциал
Потенциал — это энергия ,которая затрачивается для перемещения заряда из одной точки в другую.
φ = |
п |
|
φ = |
|
|
п |
, |
|
– потенциальная энергия заряда. |
|
– потенциал однородного поля. |
Разность потенциалов — работа, которая затрачивается для перемещения заряда.
Работа в электростатических полях
Работа, совершаемая перемещением заряда вдоль замкнутого контура внутри потенциального
поля равна нулю.
Связь между напряженность и потенциалом
= − |
|
φ |
, где ( |
|
) – набла |
Связь напряженности с потенциалом: → |
|
|
Доказывается это с учетом связи между силой и потенциальной энергией:
=− п; |
|
=− ( |
) |
|
|
|
|
|
|
|
|
|
|
=− φ |
п |
|
, подставив это в |
|
формулы |
напряженности и потенциала, |
|||||
|
|
|
=− ( φ |
+ |
φ |
+ |
φ |
) |
||||
получим: |
|
|
, векторная форма(?): → |
|
|
→ |
|
→ |
|
→ |
||
Таким образом находится связь потенциала и напряженности. Знак минус говорит о том, что вектор напряженности направлен в сторону уменьшения потенциала электрического поля. Градиент помогает определить как изменяется скорость относительно каждой из оси. Градиент можно назвать еще как “оператор Гамильтона” или набла ( ).
Теорема о циркуляции
Электростатическое поле характеризуется циркуляцией его вектора напряженности по замкнутому полю и равняется нулю.