
- •Тест
- •Свойства (мат ожидание)
- •Дисперсия
- •Свойства (дисперсия)
- •Свойства (ковариация)
- •Корреляция
- •Решение
- •Решение
- •Решение
- •Вопросы Литвиновой
- •Парная регрессия
- •Основные свойства парной регрессии
- •Пример использования
- •Множественная регрессия
- •Параметрические критерии
- •Непараметрические критерии
- •Теория mathprofi
- •Линейный коэффициент корреляции
- •Ковариация
- •Дисперсии
- •Корреляция
- •Коэффициент детерминации (множественной тоже)
- •Коэффициенты уравнения регрессии
- •Вычисление коэффициентов для регрессионного уравнения (матричный способ)
- •Коэффициент эластичности
- •Бета-Коэффициент (это другое!)
- •Коэффициент множественной корреляции
- •Очистка влияния одного фактора на другой
Товарищи, пользуемся формулами! Верхняя панель – Вставка – Формула.
Для удобства советую пользоваться LaTeX сокращениями через обратный slash “ \ “,
полный список доступных сокращений: Google Docs Equation Editor Shortcuts
Также есть удобное LaTeX расширение, во много раз упрощающее пользование формулами: Auto-LaTeX Equations - Google Workspace Marketplace
***вместо \bar советую использовать \overline
***вместо “ * ” используйте \cdot
***весь текст Arial 12 кегль.
Тест литвиновой
Вопросы литвиновой
Теория mathprofi

Тест
1.Пусть 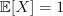 и
и 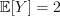 Найти
Найти 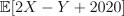
Свойства (мат ожидание)
1.
2.
3. Если 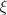 и
и  независимы, то
независимы, то 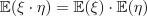
типо 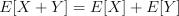 и
и 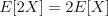
2.Пусть 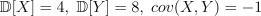 . Найдите
. Найдите 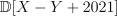
Дисперсия
Свойства (дисперсия)
1.
2.
3. Если 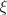 и
и 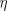 независимы, то
независимы, то 
4.
5.
Свойства ковариации (если ковариация не равна 0, то величины зависимы, иначе независимы):
2. |
(ξ, η) = (ξ · η) − ξ · η |
1. |
(ξ, ξ) = ξ |
3. |
|
4. |
(ξ + ; η + ) = (ξ, η) |
5. |
( ξ, η) = · (ξ, η) |
|
(1ξ + 1η + 1; 2ξ + 2η + 2) = |
= 1 2ξ + 1 2 η + (1 2 + 2 1)(ξ, η), где – дисперсия
6. ξ, η − независимые → (ξ, η) = 0
(ξ, η) = (ξ · η) = ξ · η = ξ · η − ξ · η = 0
7. |(ξ, η)| ≤ |
ξ · η |

Применим свойство: 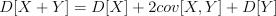
Применим свойство ковариации: 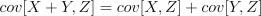
3.Пусть 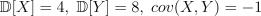 . Найдите
. Найдите 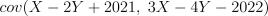
Свойства (ковариация)
2. |
(ξ, η) = (ξ · η) − ξ · η |
1. |
(ξ, ξ) = ξ |
3. |
|
4. |
(ξ + ; η + ) = (ξ, η) |
5. |
( ξ, η) = · (ξ, η) |
|
(1ξ + 1η + 1; 2ξ + 2η + 2) = |
= 1 2ξ + 1 2 η + (1 2 + 2 1)(ξ, η), где – дисперсия
6. ξ, η − независимые → (ξ, η) = 0
(ξ, η) = (ξ · η) = ξ · η = ξ · η − ξ · η = 0
7. |(ξ, η)| ≤ |
ξ · η |
Решение:
4.Пусть 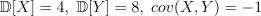 . Найдите
. Найдите 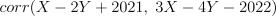
Корреляция
Решение

5.Пусть случайная величина 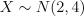 . Найдите
. Найдите 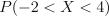
Решение
Из исходных данных получаем, что 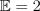 и
и 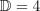
Подставим эти значения в формулу: 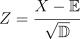
Подставив граничные значения, получаем, что 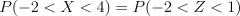
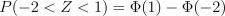 далее нужна таблица значений стандартного нормального распределения. Ответ: 0.819.
далее нужна таблица значений стандартного нормального распределения. Ответ: 0.819.
6. Пусть случайная величина 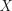 имеет стандартное нормальное распределение. Чему
имеет стандартное нормальное распределение. Чему
равна точка  , для которой вероятность
, для которой вероятность 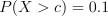
Решение
Есть формула:

7. Пусть случайная величина 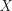 имеет
имеет  -распределение с тремя степенями свободы. Чему
-распределение с тремя степенями свободы. Чему
равна точка  , для которой вероятность
, для которой вероятность 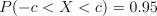
По правилу симметричности: 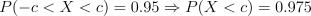
Согласно таблице  -распределения с тремя степенями работы квантиль
-распределения с тремя степенями работы квантиль 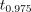 примерно равен
примерно равен
3.182
8.Пусть 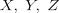 – независимые стандартные нормальные величины. Какое
– независимые стандартные нормальные величины. Какое
распределение имеет случайная величина 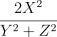 ?
?
Если величины являются стандартными и независимыми, тогда они принадлежать распределению Фишера.
Если 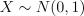 , то
, то 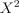 имеет распределение
имеет распределение 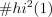 с одной степенью свободы
с одной степенью свободы
Если 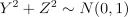 и независимы, то
и независимы, то 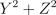 имеет распределение
имеет распределение  с двумя степенями
с двумя степенями
свободы
Если 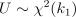 и
и 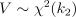 , и они независимы, то отношение
, и они независимы, то отношение 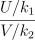 имеет распределение
имеет распределение
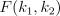 - распределение Фишера с параметрами
- распределение Фишера с параметрами 
Таким образом, искомая величина имеет распределение 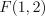

9. Пусть 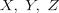 – независимые стандартные нормальные величины. Найдите
– независимые стандартные нормальные величины. Найдите
вероятность 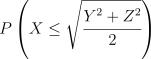
КРЧ КАКАЯ ТО ХУЙНЯ
10. Пусть случайный вектор 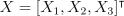 имеет ковариационную матрицу
имеет ковариационную матрицу 
. Найдите 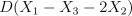

11. Пусть случайный вектор 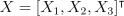 имеет ковариационную матрицу
имеет ковариационную матрицу 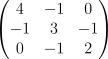 .
.
Найдите 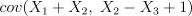
ковариационная матрица имеет вид:
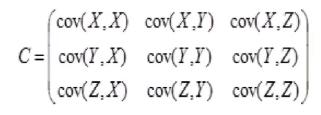 , где cov[X,X] = D[X], cov[Y,Y] = D[Y], cov[Z,Z] = D[Z]
, где cov[X,X] = D[X], cov[Y,Y] = D[Y], cov[Z,Z] = D[Z]
Уберем константу (+1) так как она не влияет на результат
Воспользуемся свойством линейности ковариации, упростим выражение, затем по таблице ковариации узнаем значение соответствующих ковариаций:
12. Пусть задана регрессионная модель 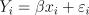 со следующими наблюдениями. Чему
со следующими наблюдениями. Чему
равна МНК-оценка параметра 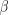 ?
?
Наблюдения:
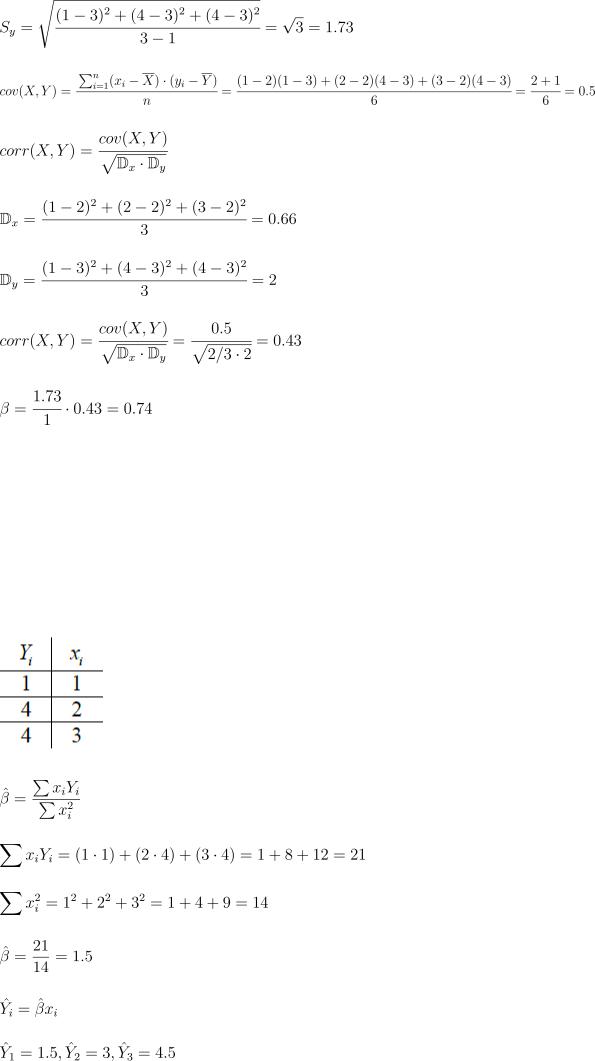
в расчетах я ошибся, но формулы вроде те, главное следить, чтобы корреляция была от -1 до
1
13. Пусть задана регрессионная модель 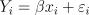 со следующими наблюдениями. Чему
со следующими наблюдениями. Чему
равен вектор МНК-прогнозов (макс максбетов) 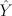 ?
?
Наблюдения:
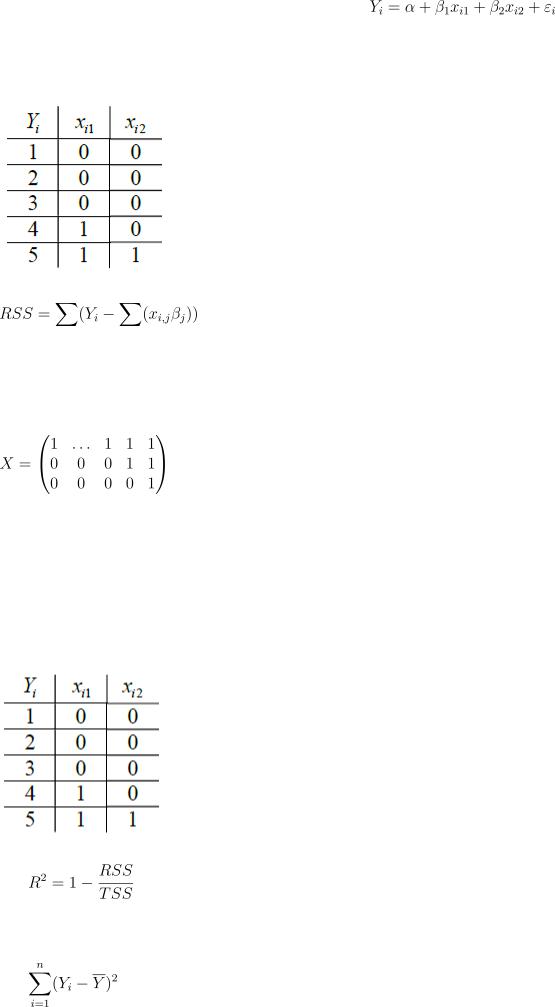
14. Пусть задана регрессионная модель |
со следующими |
наблюдениями. Чему равна сумма квадратов МНК-остатков  ?
?
Наблюдения:
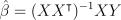 – МНК-оценка
– МНК-оценка
Для применения формулы выше, создаем матрицу-регрессор:
ипо формуле считаем МНК-оценку. Затем подставляем в первую формулу и получаем ответ.
15.Пусть задана регрессионная модель 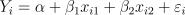 со следующими наблюдениями. Чему равен коэффициент детерминации
со следующими наблюдениями. Чему равен коэффициент детерминации 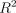 ?
?
Наблюдения:
TSS - общая сумма квадратов, рассчитывается как:
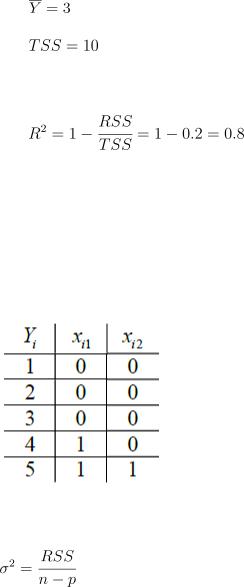
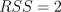 (В 16 задании алгоритм нахождения)
(В 16 задании алгоритм нахождения)
16.Пусть задана регрессионная модель 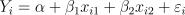 (причем
(причем
 ) со следующими наблюдениями. Чему равна несмещенная оценка параметра
) со следующими наблюдениями. Чему равна несмещенная оценка параметра 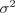 ?
?
Наблюдения:
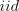 значит независимые одинаково распределённые случайные величины
значит независимые одинаково распределённые случайные величины
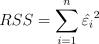 — сумма квадратов остатков (Residual Sum of Squares)
— сумма квадратов остатков (Residual Sum of Squares)
n - количество наблюдений (в нашем случае 5, количество строк)
p - количество оцененных параметров (включая свободный член  ) (в нашем случае 3, количество столбцов).
) (в нашем случае 3, количество столбцов).
Чтобы найти 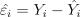 , сначала нужно оценить параметры модели (
, сначала нужно оценить параметры модели ( 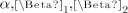 ) с использованием метода наименьших квадратов.
) с использованием метода наименьших квадратов.

После нахождения  , остатки:
, остатки:
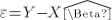 (
( 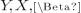 - матрицы, после вычитания получим матрицу столбец или строку)
- матрицы, после вычитания получим матрицу столбец или строку)
Найдем RSS:
17.Пусть задана регрессионная модель 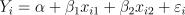 (причем
(причем
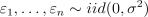 ). Дана матрица
). Дана матрица 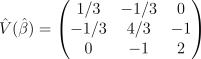 . Чему равна оценка дисперсии
. Чему равна оценка дисперсии
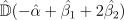 ?
?

18. Пусть задана модель линейной регрессии 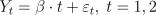 , в которой случайный ошибки удовлетворяют условиям
, в которой случайный ошибки удовлетворяют условиям 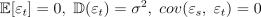 при
при 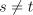 .
.
Рассматривается оценка неизвестного параметра 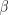 :
: 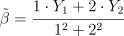 . Чему равно математическое ожидание оценки
. Чему равно математическое ожидание оценки 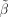 ?
?
19. Пусть задана модель линейной регрессии 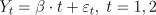 , в которой случайный ошибки удовлетворяют условиям
, в которой случайный ошибки удовлетворяют условиям 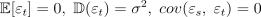 при
при 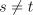 .
.
Рассматривается оценка неизвестного параметра 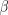 :
: 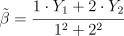 . Чему равна дисперсия оценки
. Чему равна дисперсия оценки 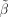 ?
?


20. Рассматривается модель  при
при 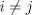 .
.
При каких значениях несмещенная оценка  имеет наименьшую дисперсию?
имеет наименьшую дисперсию?

Ответ: 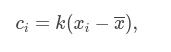
21. Рассматривается модель 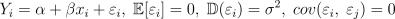 при
при 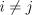 .
.
При каком условии на параметры  оценка
оценка 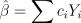 окажется несмещенной?
окажется несмещенной?

22.Пусть задана регрессионная модель 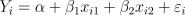 (причем
(причем
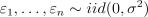 ). Пусть
). Пусть  и
и 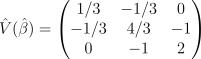 .
.
Постройте 95% доверительный интервал для параметра 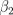 .
.

23.Пусть задана регрессионная модель 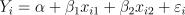 (причем
(причем
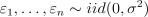 ). Пусть
). Пусть 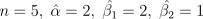 и
и 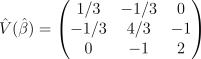 .
.
Постройте 95% доверительный интервал для 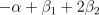 .
.

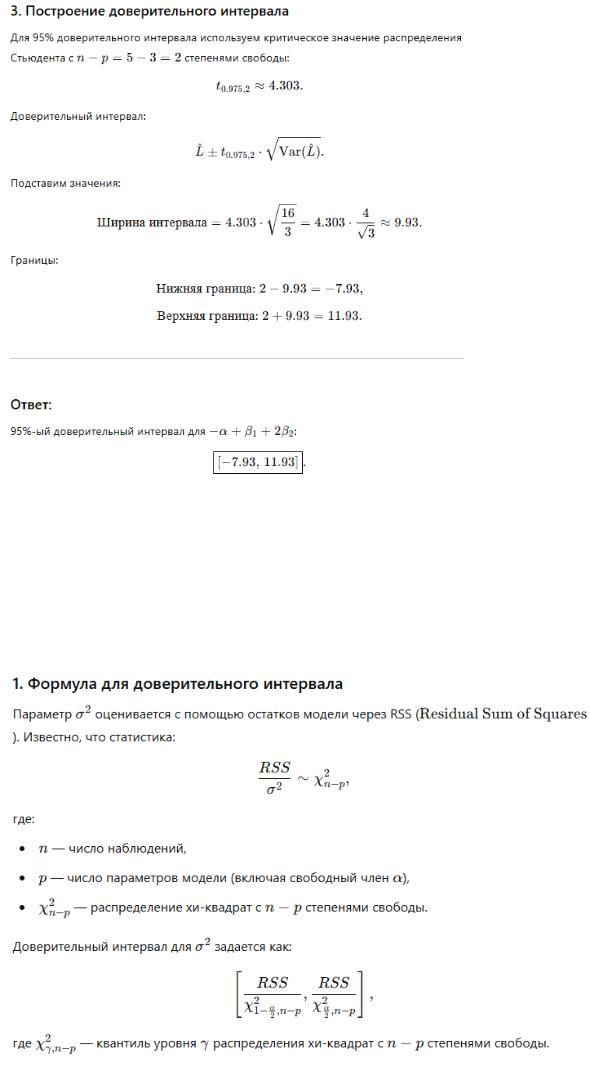
24. Рассматривается модель регрессии 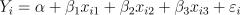 , в которой ошибки
, в которой ошибки 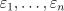 независимы и имеют нормальное распределение с нулевым математическим ожиданием и дисперсией
независимы и имеют нормальное распределение с нулевым математическим ожиданием и дисперсией 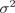 . Пусть
. Пусть  и
и 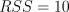 . Постройте 95% двусторонний
. Постройте 95% двусторонний
симметричный по вероятность доверительный интервал для параметра 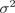 .
.

25. Оценивается зависимость уровня заработной платы работника (wage) от уровня образования (educ), общего стажа (exper) и числа лет работы у текущего работодателя
(tenure) в виде линейной регрессии 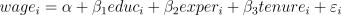 , в которой ошибки
, в которой ошибки 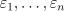 независимы и имеют нормальной распределение с нулевым математическим ожиданием и дисперсией
независимы и имеют нормальной распределение с нулевым математическим ожиданием и дисперсией 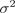 . Число наблюдений
. Число наблюдений 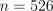 . В таблице ниже приведены результаты оценивания. На уровне значимости 5% укажите, какие из переменных (educ, exper, tenure) оказывают значимое влияние на уровень заработной платы работника.
. В таблице ниже приведены результаты оценивания. На уровне значимости 5% укажите, какие из переменных (educ, exper, tenure) оказывают значимое влияние на уровень заработной платы работника.

Таблица:
