Уравнения в частных производных первого порядка.

12. Линейное однородное уравнение в частных производных. Частное и общее решение. Интегральная поверхность. Характеристическая система. Характеристики. Теорема об общем решении.

непр. диф. в G, неизв. функция независимых переменных и выполнено условие

Опр. Уравнение (1) наз линейно-однородным уравнением в частных производных 1-го порядка, т.к. входит линейно только через свои производные.

Опр. Непр. диф. ф-ия опр. в G называется частным решениемм УЧП (1), если при подстановке в (1) она обращает его в тождество.

Опр. Совокупность всевозм. частных решений образует общее решение УЧП (1)

Опр. Если к-либо ч. решение ур (1), то пов-ть в пр-ве переменных наз. интегр. поверхностью УЧП (1).

Сопоставим ур-ию (1) систему ОДУ (автономную)

или в симм. форме

Поскольку в G явл решением УЧП (1) первый интеграл системы (3) (или(4))

Поскольку вып. усл. (2) (из которого следует, что ни одна точка области G не явл. т. покоя системы(3)) шт. ФНЗ I-инт. сист (3) (или (4)). Пусть это будут . Тогда произв. интеграл (всевозм. I-инт )системы (3) (или(4)) имеет вид : , где Ф – произвольная непр. диф. функция своих аргументов общее решение УЧП (1) будет

Опр. Сист (4) (или(3)), связ. с УЧП (1) , наз. характеристической системой, а ее решение характеристиками.

Можно заметить, что система уравнений (4) задает вект. линии поля (Поскольк вект. линии поля это линии, касательный вектор которых в каждой точке коллиниарен вектору поля) . Т.о. решение УЧП (1) сохр. пост. значение на характеристиках, т.е. вдоль вект. линий поля.

Геометрический смысл характеристик.

Пусть решение (1). Тогда это соотношение задает инт. пов-ть в . Рассмотрим уравнение , которое задает линии уровнения поверхности . На линии уровнения сохр. пост. значение, т.е. линии этой пов-ти и есть характеристики. Т. о. характеристики лин. однор. УЧП (1) являются линиями уровнения инт. пов-ти .

Пример. Пусть x,t – незав. прем. уд. уравнению . Хар. сист. : задает характеристику бег. волна. Ф- произв. непр. тдиф. функция. Вид Ф можно конкретизировать, если, например, задано .

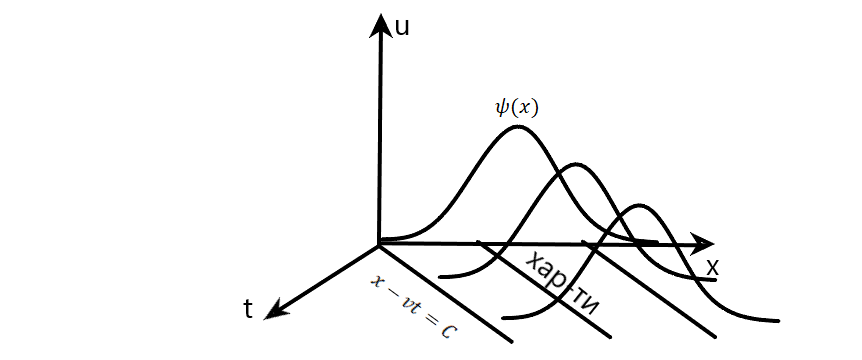
Получаем интегр. пов-ть:

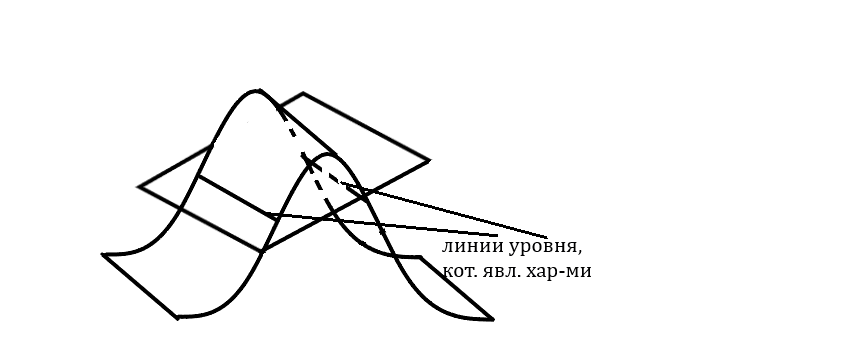
Замеч. Ур-ние (1) можно представить в виде это (по определению) – производная функции по напр. поля . То есть сам смысл ур-ия в том, что вдоль векторных линий поля и сохр. пост. знач.

13. Квазилинейное уравнение в частных производных. Частное и общее решение. Интегральная поверхность. Характеристическая система. Характеристики. Теорема об общем решении.

Рассмотрим УЧП:

непр. диф. в D, непр. диф. в D, а также вып усл

Опр. УЧП (6)и наз квазилинейным ( зависит от u ) неоднородным УЧП 1-го порядка.

Опр. Непр. диф. функция называется частным решением (1) на G, если и при подст. в (1) оно обращ в тождество.

Опр. Совокупность всевозможных ч. решений называется общим решением.

Опр. Если решение (1), то пов-ть в пр-ве назовем интегральной пов-тью.

Допустим, что решение УЧП(1) можно задать в неявном виде след. образом : , где непр. диф. в D, причем . Тогда по теореме о неявной функции, получим, что . Подставим (4) в (1), получим или это линейное однородное уравнения для неизв. функции

Этому уравнени. сопост. сист. ОДУ (авт) ((n+1) порядка) или в симм. форме которая обладает системой из n ФНЗ I-инт.

Пусть это

Всевозможные решения УЧП (5) получим из всевозможных I-инт. системы (6) (или (7)) , где Ф – произв. непр. диф. функция. Тогда общее решение квазилинейного неоднородного уравнения (6) задается соотношением , причем это нужно, чтобы (8) задавало u как неявную функцию от

Замеч. Вообще говоря, у уравнения (1) существуют решения, которые не описываются ур-ием (8) (особые решения), но мы их рассм не будем.

Опр. Системы (6),(7) наз характеристическими системами ур-я (1), а их решения характеристиками.

Замеч. Этим же способом (через неяв. фун-ию) можно решать и линейные однор. (неод) ур-ия

В этом случае хар. сист. будет. (или в случ. однор. ) (15) имеет n ФНЗ I-инт. ,… (всегда можно добиться, чтобы u не входило в первые (n-1) I-инт. )

Тогда неявное решение задается как , где Ф – произв. непр. диф. функция , тогда (16) по ТСЕ неявн. функций еще раз по ТСЕ

(для неоднородного случая

непр. дифф.

14. Геометрическая интерпретация интегральной поверхности квазилинейного уравнения.

Теор. (О геом. смысле характеристик квазилин. ур-ия)

Интегр. пов-ть квазилинейного неоднородного УЧП (1) целиком состоит из характеристик (т.е. через каждую точку прох. хар-ка целиком принадл. инт. пов-ти)

Док-во: Пусть решение () (т.е. задает в инт. пов-ть). Рассмотрим систему (**) или отвеч. ей авт систему Решение (2) задает траекторию в фаз. пр-ве (в парам. форме) , тогда задает в парам форме кривую лежащаю на инт пов-ти:

П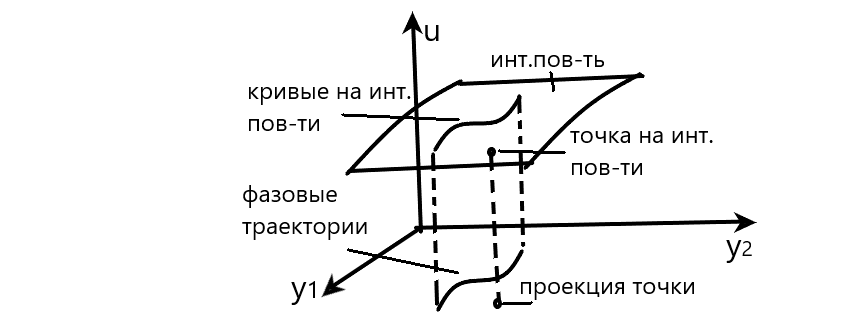 окажем, что всякая кривая, задаваемая системой (3) явл. характеристикой :

Совестно с (**) это даёт, что , т.е. (3) определяет характеристику.

Замеч. Система ур-ий (4) она задает векторные линии поля . Т.о. интегральная пов-ть квазилин. УЧП формируется вектор. линиями поля . Такие пов-ти (сформированные вект. линиями поля) называются векторными трубками, т.о. инт. пов-ть квазилинейного УЧП явл. вект. трубкой поля .

15. Задача Коши для квазилинейного уравнения. ТСЕ (обсуждение на качественном уровне)

Задача Коши для квазилинейного уранения.

Будем рассм. случай для

неизв. непр. диф. функция незав. перем.

заданные непр. диф. функции

Пусть в пр-ве задана крива Г :

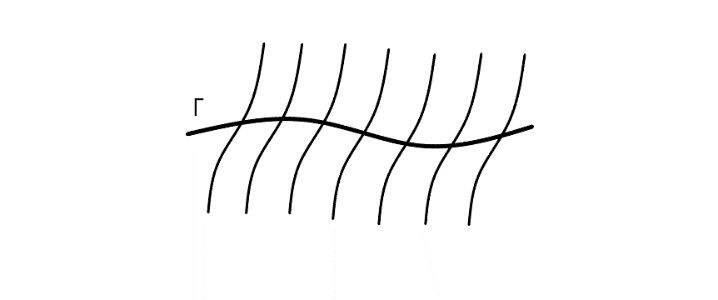Задача Коши: найти инт. пов-ть уравнения (1), проход. через кривую Г (2).

Поскольку инт. пов-ть УЧП (1) состоит их хар-к, то мы получим искомую пов-ть проведя хар-ки через каждую точку кривой Г. Они и сформируют инт. пов-ть. Проблема заключается в том, что может оказаться, что Г (или некоторый ее кусок) совпадает с хар-кой. В этом случае ЗК не будет иметь ед. реш.

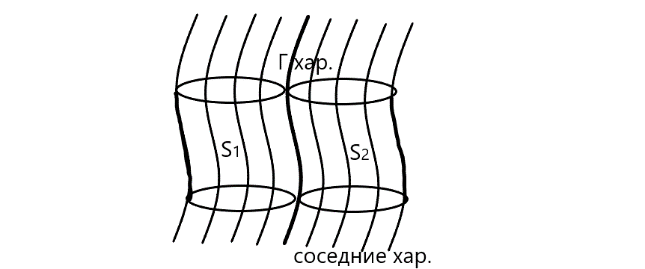
2 различные инт. пов-ти, проход. через Г(кот. явл. хар-кой)

Теор. (ТСЕ реш. ЗК)

Если Г – гладкаяя кривая ни в одной точке не касается характеристик УЧП (1), то инт. пов-ть этого ур-ия, проход. через Г.(без док-ва)

Замеч. Ур-ия характеристик имеют вид . Т.о. кас. вектор к хар-ки имеют компоненты 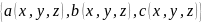и условия не касания кривой Г характеристики приобретают вид усл. отражает не коллинеарнгость кас. век-ров характеристик и кривой Г

16. Алгоритмы решения Задачи Коши в случае неявного или параметрического задания поверхности.

1. Пишем хар. систему и находим 2 ФНЗ I-инт. этой системы. Пусть это будут . Тогда где Ф – произв. непр. диф. фун-ия : задает в неявном виде обшее решение (1) т.е. в неявном виде задает всевозможные инт. пов-ти. Нас интересует только та, которая проходит через Г. обозначим ф-ию, кот. она задается неявно буквой .

2. Поскольку искомая инт. пов-ть проходит через Г, то .

Фактич. Ф задает связь между и . Нам их всевоз. связей нужно найти ту, которая задает искомую инт. пов-ть. Эту связь мы получим, если из сист. исключим параметр t. В результате этого исключения получим связь вида .

3. Тогда задает искомую инт. пов-ть (в неявном виде)

Замеч. Не всегда кривая Г задается параметрически. Если Г задана как пересеч. гладких пов-тей : В этом случае алгоритм решения ЗК след:

1. Нашли ч. ФНЗ I-инт.

2. Из системы исключаем x,y,z и получаем связь между в виде

3. задает искомую пов-ть (в неявном виде)