Глава. Теория устойчивости.

1. Определение устойчивости по Ляпунову решения системы ОДУ первого порядка. Асимптотическая устойчивость.

Рассмотрим норм. систему ОДУ

или кратко

Далее считаем, что функции опр. и непр. В . Пусть Рассмотрим ЗК Будем для простоты считать, что решение ЗК существует 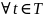и оно не выходит из области D при . Обозначим решение ЗК с н.у. след.образом . Рассмотрим вместе с ним решение ЗК, удов. другому н.у. . Т.е.

Опр. Решение ЗК называется устойчивым по Ляпунову, если

Совокупность вектор столбцов(строк) функций с обычными операциями сложения и умножения на числа, образ. ЛП, в котором можно ввести норму, например,

Если , что какое бы малое мы бы ни взяли при том, что найдется то решение будет неустойчивым.

Опр. Решение называется асимптотически устойчивым, если :

1. Оно устойчиво по Ляпунову

2. 

Замеч. Можно показать, то уст. и ас. уст. не зависит от выбора , поэтому в дальнейшем считаем

Исследование устойчивости нетривиального решения исходной системы можно свести к исследованию устойчивости тривиального решения модифицированной системы.

Пусть решение удовлетворяющее условию . Рассмотрим . Тогда т.е. реш. системы (1) переходит в решение системы (4).

При этом отклонение

Т. о. вопрос об устойчивости решения ЗК сводится к вопросу об устойчивости тривиального решения системы , где

Далее считаем, что система облад. трив. решением и запишем исслед. уст. и ас.уст. именно тривиального решения.

Рассмотрим систему , обладающую тривиальным решением.

Опр. Тривиальное решение называется устойчивым по Ляпунову, если

Опр. означает, что тривиальное решение неустойчиво

Опр. Тривиальное решение называется ас.уст., если :

1. Оно устойчиво по Ляпунову

2. 

2. Теорема о устойчивости и асимптотической устойчивости решения линейной системы с постоянными коэффициентам (доказательство для случая простых вещественных отрицательных корней). Фазовое пространство. Фазовые траектории. Фазовый портрет. Точки покоя (положения равновесия).

Теор. постоянная матрица с действ. коэф.; орни хар. ур-ия . Тогда:

1) Если , то тривиальное решение ас. уст.

2) Если , то тривиальное решение неустойчиво.

3) Если , причём то тривиальное решение устойчиво но не асимпт.

4) Если и

1) Док-во для отрицательных вещественных корней: prav

Пусть общее решение системы (1) имеет вид:

,

Выразим через нач. условия . Строим биортогональную систему . - базис и

- СЛАУ относительно , которая совпадает с матрицей Грама базиса реш , т.е числа опред ед. образом.

Аналогично строим эл-ты . Умножая последовательно (3) на получим , тогда

. Докажем теперь асим устойчивость. уст асимпт. #

2) Док-во (Иванова): Докажем для случая 1), считая, что у каждого совпад геом и алг кратности, т.е каждому k-кратному корню хар. ур-ия отвеч k ЛНЗ СВ матрицы А.

Пусть действ корни, комплек корни.

Строим действ ФСР в виде

Пусть это будут элементы

далее обозначим . Тогда есть ФСР , причем все .

Обозначим

Выразим константы через нач условия ЗК, т.е через значения , т.е. . Для этого построим биортогональную систему . Разложим (это базис, поэтому возможно) : (1) чтобы найти неизв. коэф. Разлож. (1) умножим послед скалярно на тогда получим :

…

получили СЛАУ (неоднор) с матрицей

которая совпад с матриц Грама базиса реш , т.е числа опред ед образом. Аналогично стрим эл-ты . Т.о. биортогональная система построена. Теперь рассмотрим : . Умножим (2) пос-но скалярно на . Получим : . Т.е. . Оценим

Т.о. . . Т.о. . Значение выберем след образом : . Тогда . Т.о решение уст по Ляпунову. Докажем теперь асим устойчивость. уст асимпт. # Остальные пункты (и даже этот когда АК>ГК) без док-ва.

Далее эти случаи будут рассм. на примере системы 2-го порядка.

Рассмотрим систему , т.е. не зависит от t. Такие системы называются автономными. Рассмотрим некоторое решение этой системы. При изменении t точка описывают в кривую, назыв. интегральной кривой.

Если в пр-ве перем. рассм. подпространство переменных , то при изменении t, точка также описывает в этом подпространстве некотору. кривую, которая называется фазовой траекторией, а само пр-во перем. называется фазовым подпространством. Т.е. фазовая траектория это проекция интегральной кривой на фазовое подпространство.

Д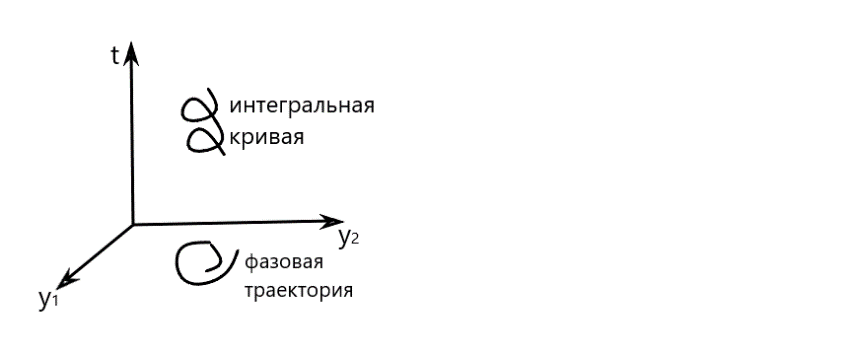 вижение точки по фазовой траектории в фазовом подпространстве при увеличении t обозначается стрелками.

Опр. Точка фазового подпространства называется точкой покоя (полож. равновесия) автономной системы (1), если при этом явл. стац. реш.). Возникает вопрос об устойчивости т. покоя. Вопрос об устойчивости ненулевой точки покоя можно путем замены переменных свести к вопросу об уст. нулевой т.покоя поэтому далее считаем

Опр. Совокупность фазовых траекторий, дающих представление о решениях системы, называется фазовым портретом.

3. Автономные и неавтономные системы. Сведение неавтономной системы к автономной и наоборот. Симметричная форма записи автономной и неавтономной систем

Рассмотрим систему , т.е. не зависит от t. Такие системы называются автономными. Рассмотрим некоторое решение этой системы. При изменении t точка описывают в кривую, назыв. интегральной кривой.

Если в пр-ве перем. рассм. подпространство переменных , то при изменении t, точка также описывает в этом подпространстве некотору. кривую, которая называется фазовой траекторией, а само пр-во перем. называется фазовым подпространством. Т.е. фазовая траектория это проекция интегральной кривой на фазовое подпространство.

Д вижение точки по фазовой траектории в фазовом подпространстве при увеличении t обозначается стрелками.

Опр. Точка фазового подпространства называется точкой покоя (полож. равновесия) автономной системы (1), если при этом явл. стац. реш.). Возникает вопрос об устойчивости т. покоя. Вопрос об устойчивости ненулевой точки покоя можно путем замены переменных свести к вопросу об уст. нулевой т.покоя поэтому далее считаем

Опр. Совокупность фазовых траекторий, дающих представление о решениях системы, называется фазовым портретом.

Вернемся к

Далее считаем, что все 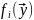непрерывны в некоторой и фазовая траектория не выходит из . Пусть, например, . Тогда , тогда автономную систему можно привести к неавтономной системе, уменьшив кол-во неизвестных. в самом деле из получаем, что Поскольку в , то в ок-ти получаем эквивалентную систему в которой выступает в качестве нового независимого переменного. Число уравнений на 1 уменьшилось, но система стала неавтономной. Можно, наоборот, привести неавт. систему к авт. увеличив на 1 кол-во функций.

Пусть имеется неавтономная система

Положим , тогда получим эквивалентную систему 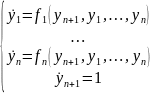эта система уже автономная, но ее порядок на 1 выше.

Далее займемся изучением автономных систем 2-го порядка с постоянными коэффициентами.

которая при эквивалентна одному уравнению , а при эквив. одному ур-ию . И обратно, всякое ур-ие вида (11) или (12) сводится к автон. сис-ме (10).

4. Простейшие типы точек покоя автономной линейной системы 2-го порядка с постоянными действительными коэффициентами (подробно, с переходом в базис, в котором траектории имеют простейший вид): бяк бяк

Займемся изучением тривиальной точки покоя системы (10). Рассм. хар. ур-ие . Пусть его корни.

Пусть (корни действительные, различные, отрицательные)

. Рассмотрим поведение решения на фазовой плоскости.

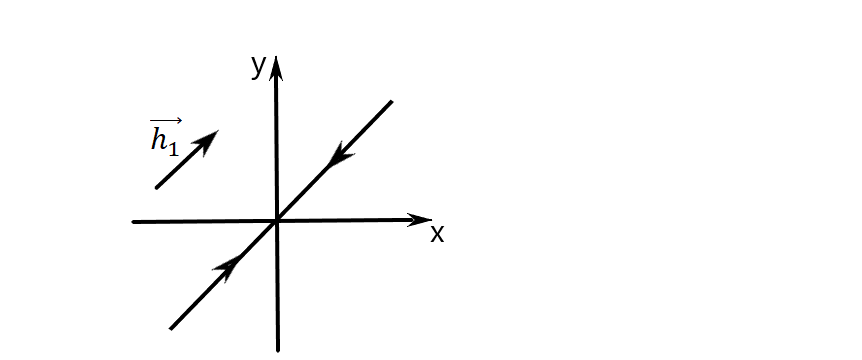Пусть , тогда или прямая на пл-ти с напр. век-ом . Поскольку , то по мере увеличения t, затухает.

т.е. при увеличении t точки на этой фазовой траектории стремятся к точке покоя (положению равновесия)

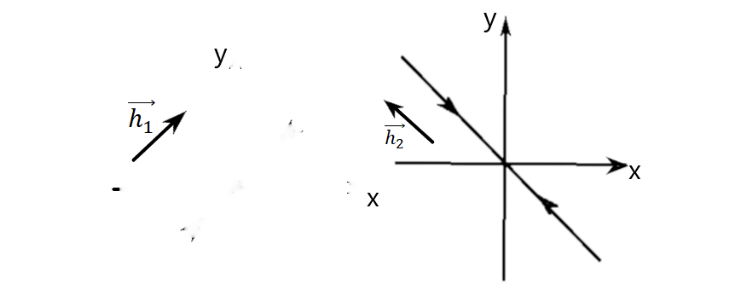
Аналогично, если

или прямая на пл-ти с напр. век-ом .

, то по мере увеличения t движутся в направлении точки покоя

Пусть

⇒ (движ. к т. покоя)

⇒

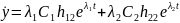то 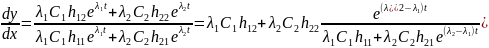. Пусть , тогда фазовая траектория при касаются прямых траекторий, отвечающих направлению вектора , т.е. СВ, отвечающий меньшему по модулю СЗ . Поскольку то эта точка покоя. асимптотич. уст.

О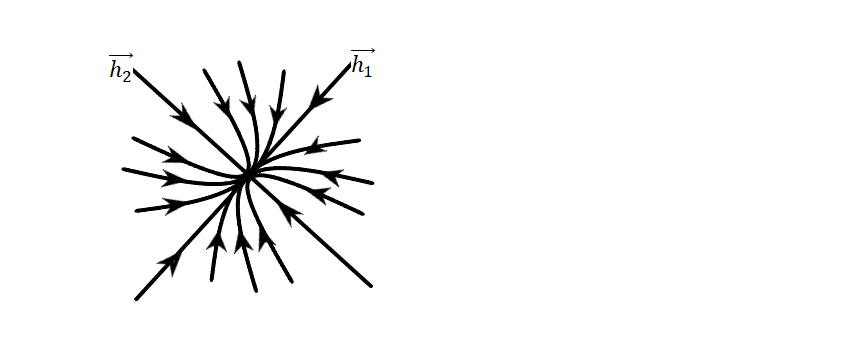 пр. Такая точка называется устойчивый узел.

устойчива она, так как решения близкие в любой момент времени остаются близкими при

Перейдем из ОНБ к базису . В этом базисе имеет координаты (1,0), а (0,1). Следовательно, в этом базисе , т.е.

в новой системе координат, тогда

Хар. ур-ие : система имеет те же корни хар ур-ия.

С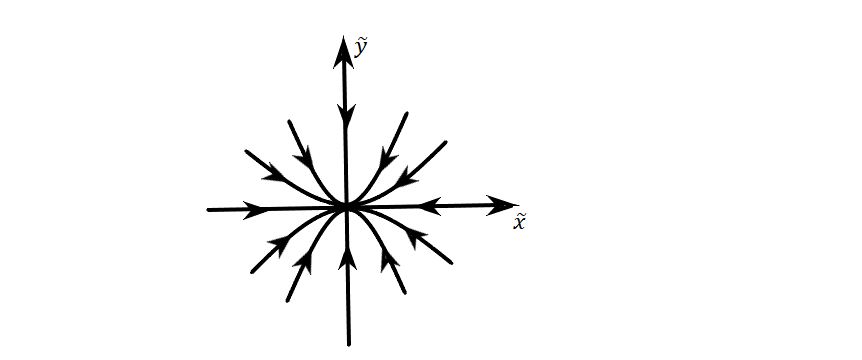 увеличением t движение идёт к т. покоя

В новой системе координат

При возвращении в исх. базис происходит деформация

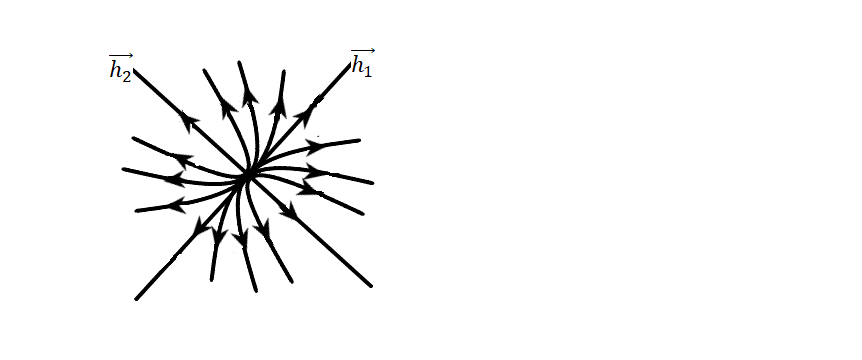
Этот случай получается из предыдущего (замена )

Такая точка покоя неустойчива и называется неустойчивым узлом

движение в направлении точки покоя по прямой

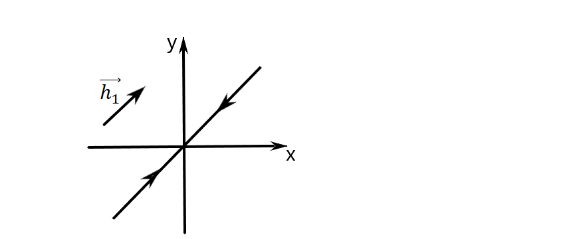
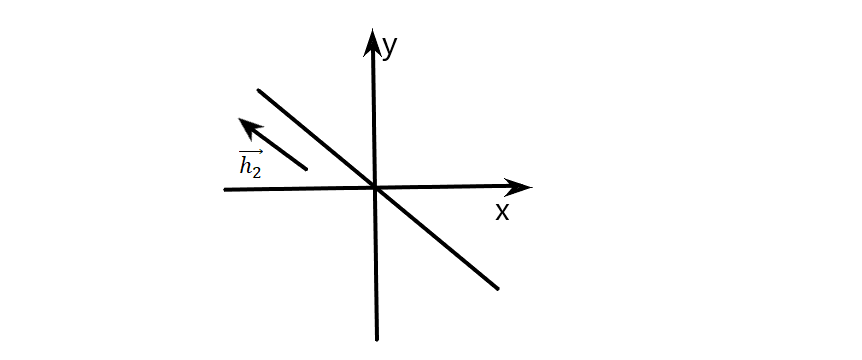
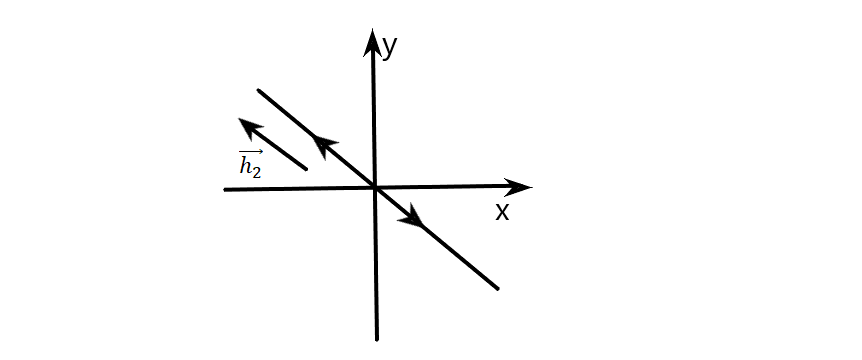
точки разбегаются по прямой от т. покоя

Перейдём в базис из СВ

, т.е.

К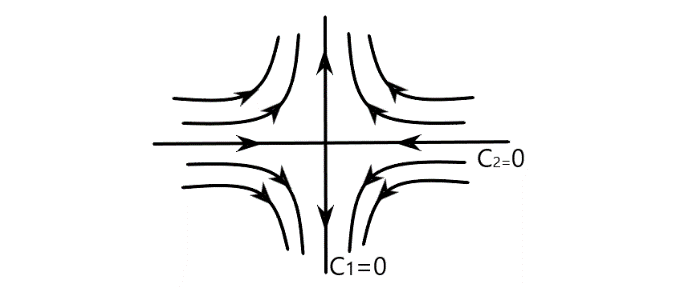 ак бы близко при т. = ни находилась к т. покоя, при она по гиперболич. траектории уйдет от т. покоя (исключение – точка на прямой )

Такая точка покоя называется седлом, она является неустойчивой.

В старой системе:

У этих гипербол асимптоты -

строки матрицы А пропорциональны, т.е.

фазовые траектории – прямые

Е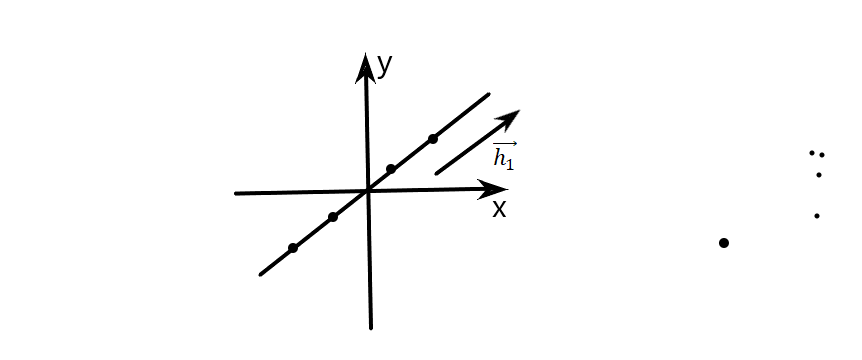 сли , то т. покоится (вся прямая состоит из т. покоя)

Если т. на прямой

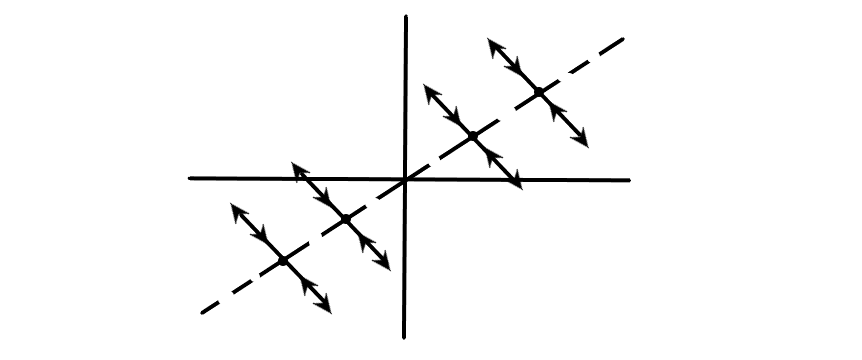
неустойчивые точки покоя

устойчивые точки покоя (но не асимптотически, т.к. находясь на произвольной прямой необязательно попадем в (0,0) (но будет к ней приближаться))

Случай различных комплексно-сопряжённых корней

Матрица действительная различные СВ для раз. СЗ

Пусть это

Переход в базис

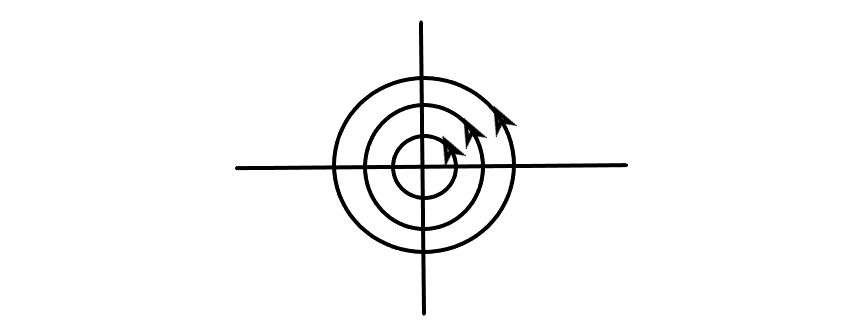
точка покоя называется центром устойчивым, но не асиптотически

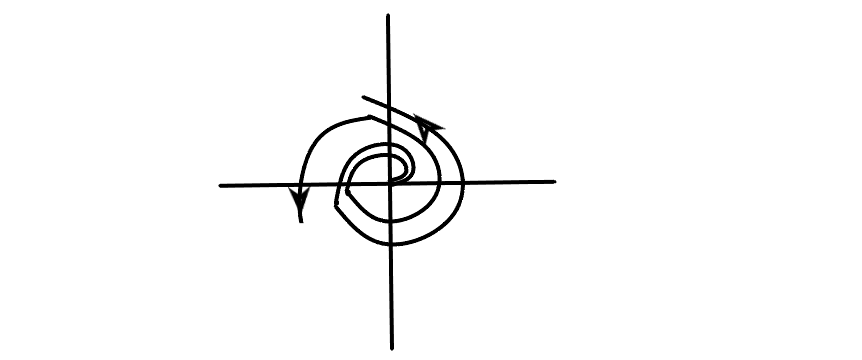
Точка называется неустойчивым фокусом

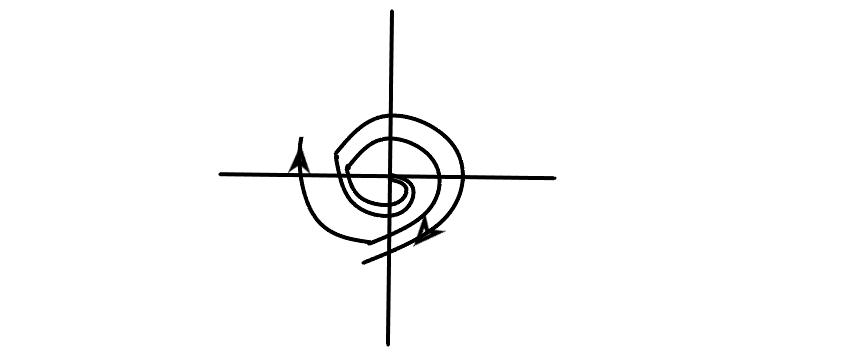
Точка называется неустойчивым фокусом

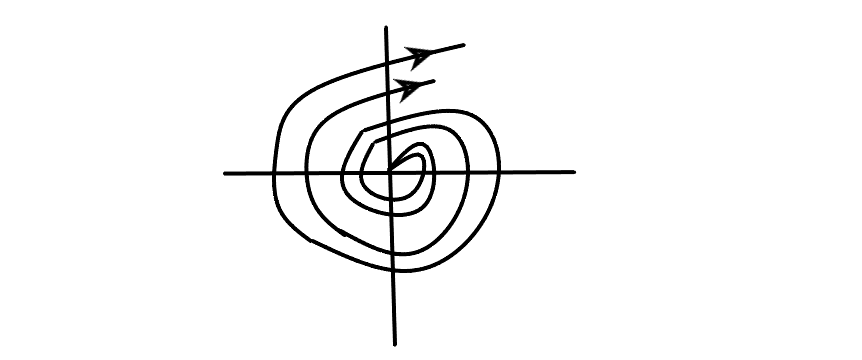
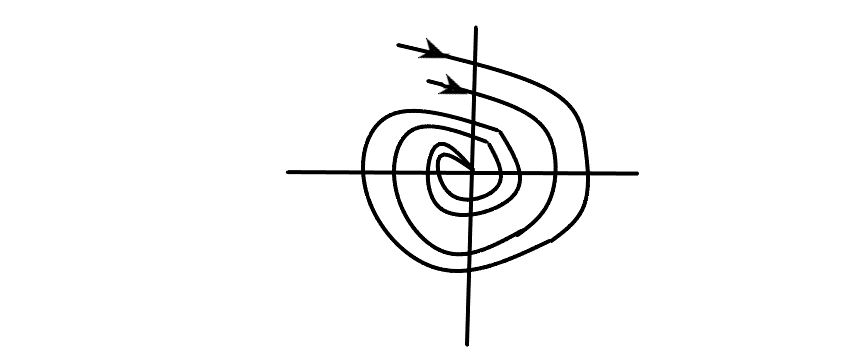
Устойчивый фокус(причем асимптотически)

В исходной системе координат – соосные эллипсы

квадрат расстояния от т. (x,y) до т. покоя (0,0)

достигает максимума на одной оси и минимума на другой

тангенсы угла наклона прямых на которых расположены оси эллипса

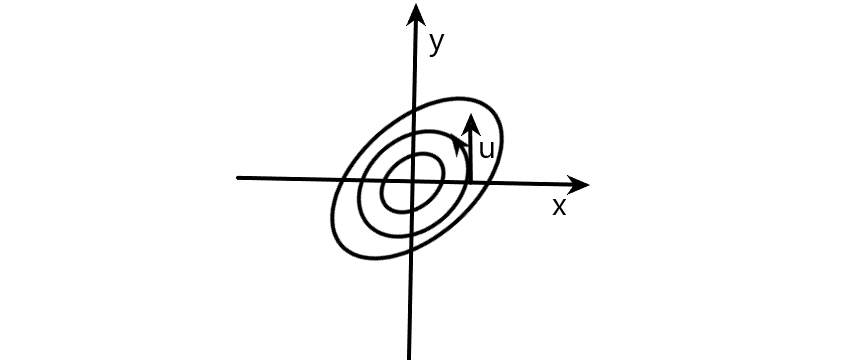Возвр. обратно

Центр (устойч., но не асим.)

Н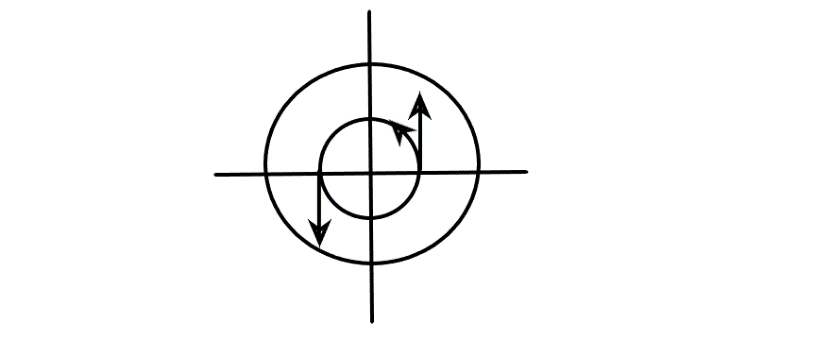 аправление движения по фазовым траекториям всегда можно определить по вектору скорости , посчитанному в любой точке, не являющейся точкой покоя

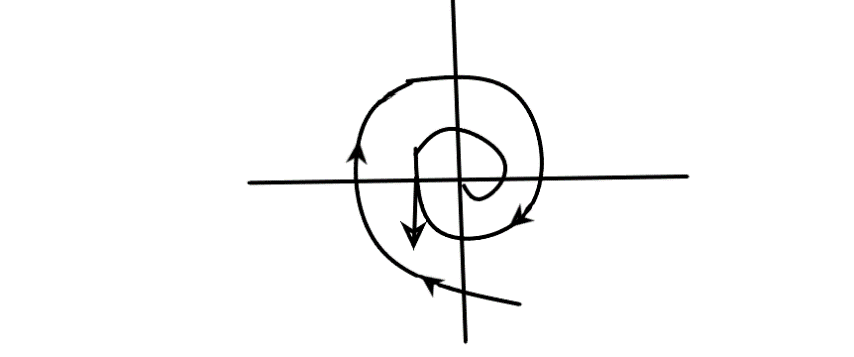
неустойчивый фокус

устойчивый фокус