Билеты ряды Горячев

Метод Фейера

(При верно, если вместо под-ки орг-ть пред. переход при )

Рассмотрим сумму Фейера

Ядро Фейера (арифметическая сумма ядер Дирихле)

Упростим:

=

Тогда запишем:

При предельный переход

Свойства ядра Фейера:

1. 

2. 

3. 

1-3 следует из ф-лы

4. 

5. 

#

-У ядра Дирихле можно док-ть аналогичное 5-е св-во, но это не нужно

-Св-вом 1 ядро Дирихле не обладает

Т5. (Теорема Фейера)

Док-во:

Но

Суммы Фейера сх-ся к ф-ии равномерно, а значит, и в каждой точке

Если ряд Фурье от непр. периодич. ф-ии нужно просуммировать по методу средних арифм. чтобы восстановить ф-ию.

Т6. (Теорема Вейерштрасса)

Триг. с-ма

Док-во:

Возьмем

Сл.

Док-во:

Т7.

Док-во:

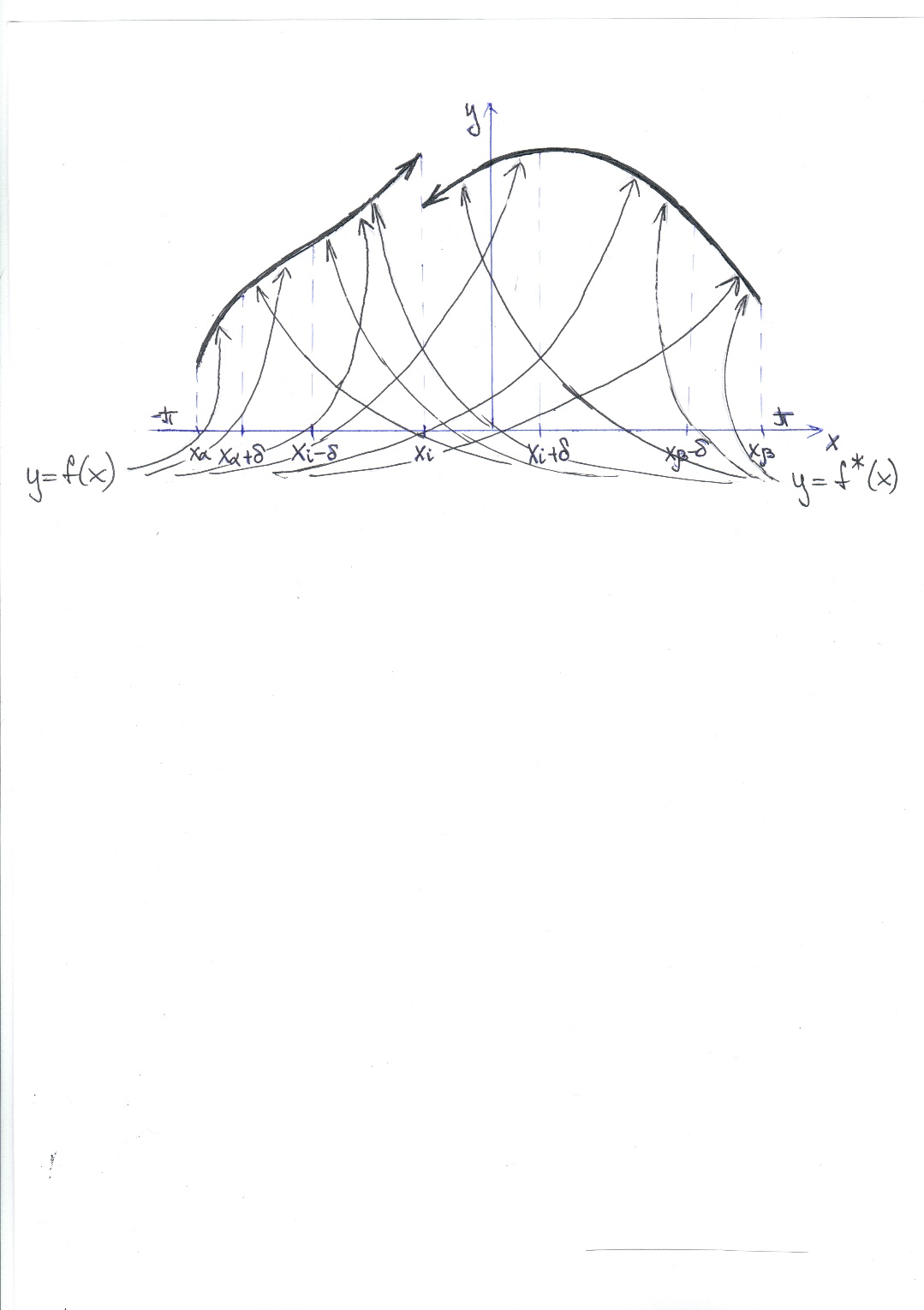
Соединим по прямым линиям соотв. знач.

Приблизили

Т.к.

Насколько близки друг к другу f и f ^*?

( приближ. со степ. точками)

Сл.

Док-во:

Сл. Тригонометрический ряд Фурье можно почленно интегрировать, таким образом получим поточечно сходящийся ряд.

Док-во:

Сл. prav

# #

Т8.

Док-ва:

prav

=

.

.

.#

Т9.

- послед-ть част.сумм – рассматриваем, сходится она поточечно, равномерно или в смысле

Док-во:

Интеграл и преобразование Фурье.

Опр. , опред при назыв регулярной, если :

1. 

2. имеют конечное число т.р. 1-го рода, причем осреднена в своих т.р.

Т1. регулярная

Док-во: Надо доказать , что

. . Обозначим . фикс. Параметр . .

.

На (по лемме Римана) , т.е. , т.е

Аналогично, #

Интеграл Фурье.

Комплексная форма интеграла Фурье.

(v.p. гл значение Коши)

преобразование Фурье (прямое и обратное)

Т1’. регулярная , причем

Это – другая формулировка Т1.

Если , то после симм продолжения :

четное продолжение

нечетное продолжение

Поэтому можно ввести :

косинус-преобразование Фурье

синус-преобразование Фурье

При этом :

, т.е. эти преобразования взаимо обратны.

Пусть имеют конечное число т.р. 1-го рода, причем осреднена в своих т.р.

Пусть интегральная сумма )

Свойства преобразования Фурье

F[f]= , =

f(x)-прообраз оригинала; - образ изображения

1. Линейность, т.е. F[αf+βg]=αF[f]+βF[f]

2. Ограниченность, т.е. ∃M>0: | |

Док-во: #

3. f(x): f(x),f’(x),…, непрер. и абс. интегрир. на (-∞,+∞), причем

Док-во: =

, k=0,1,…,m.

=>

#

4. непр на абс инт на непр на , причем

Док-во:

св-во 4 верно.

св-во 4 верно.

и т.д. m раз дифф по параметру. #

Свертка и преобразование Фурье.

Опр. непр, орг и абс интегр на свертка

1. Свертка непр , орг и абс интегрируема

Док-во:

, т.е и по

орг.

, . Можно доказать, что

сх можно переставить пределы интегр

, т.е f(x) абс интегр #

2. 

Док-во: #

3. без док-ва

4. 

Док-во: