Maths / Quadratics- rectangular hyperbolas

Quadratics/Rectangular Hyperbolas

The quadratic function is of the form:

y = ax² + bx + c a,b & c are contents

Expanding quadratics (i.e. removing brackets)

Example (x + 2) (x + 3)

= x (x + 3) + 2 (x + 3)

= x² + 3x + 2x + 6

= x² + 5x + 6

Example (x - 3) (x + 2)

= x (x + 2) + -3(x + 2)

= x² + 2x - 3x - 6

= x² - x – 6

Practice Expansion

1. (x - 9) (x + 2)

2. (4 - x) (x + 1)

3. (2x - 6) (x + 3)

4. (x - 3) (x - 4)

Answers:

1. (x - 9) (x + 2)

= x (x + 2) + 9 (x + 2)

= x² + 2x - 9x – 18

= x² - 7x – 18

2. (4 - x) (x + 1)

= 4 (x + 1) + -x (x + 1)

= 4x + 4 - x² – x

= - x² - 3x + 4

3. (2x - 6) (x + 3)

= 2 x (x + 3) + -6 (x + 3)

= 2x² + 6x -6x – 18

= 2x²-18

4. (x - 3) (x - 4)

= x (x - 4) + -3 (x - 4)

= x² + 4x -3x + 12

= x² -7x + 12

Solving Quadratic Equations

Finding the x values such that y = ax² + bx + c = 0 is a useful skill to have.

We solve it with the quadratic formula:

x =

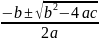
Example Solve 2x² + 3x – 5 = 0

a = 2

b = 3

c = -5

x =

=

=

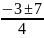
ie. Either x = or x =

= =

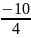
= 1 = -2.5

Practice Questions

Solve for x

1. x² + 3x + 2 = 0

2. 3x² + 2x – 5 = 0

3. -3x² + 2x – 5 = 0

4. -2x² + 2x + 5 = 0

5. 5x² – 4x – 10 = 0

Answers

1. a = 1

b = 3

c = 2

x =

=

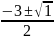
ie: either x = or x =

= =

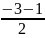
= -1 = -2

2. a = 3

b = 2

c = -5

x =

=

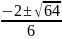
ie: either x = or x =

= 1 x = -1.67

3. a = - 3

b = 2

c = -5

x =

=

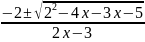
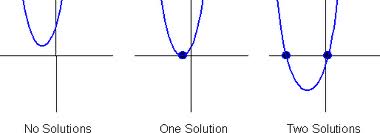
Therefore: No solutions

4. a = -2

b = 2

c = 5

x =

=

=

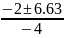
ie: either x = or x =

= =

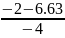
= -1.16 = 2.16

5. a = 5

b = -4

c = -10

x =

=

=

ie: either x = or x =

= 1.87 = -1.07

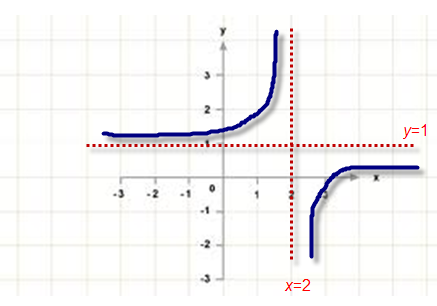
Rectangular Hyperbolas

The basic reciprocal function y = is:

Both the x axis and the y axis are asymptotes

Example Sketch the function

y + 1

• The asymptotes change to y = 1 and x = 2