Maths / Matrices

Matrices

A matrix is simply an array of numbers

Example:

Broncos Titans St George Canberra

Week 1 2 2 1 0

Week 2 0 0 0 0

Week 3 2 0 2 2

The above information on points earned in the National Rugby League competition for the first 3 weeks of competition can be represented by:

The matrix has 3 rows and 4 columns so we say it has the order 3 x 4 (3 by 4). The order of the matrices is given as rows by columns.

Practice Questions

List the order of these matrices

(1)

(2)

(3)

(4) (1 2 3)

(5)

Answers

(1) 2 X 3

(2) 2 x 2

(3) 3 x 2

(4) 1 x 3

(5) 3 x 1

Addition, Subtraction and Scalar Multiplication

Note: Matrices have to be of the same order before we can add and subtract them

Example: A = B =

Calculate:

(1) A + B

(2) A - B

(3) 3A

(4) 2B + 4A

Answers

(1) A + B = +

= (Add together the numbers in the same position in the matrix)

(2) A – B = -

= (Again, subtract numbers in the same position)

(3) 3A = 3 x

=

(4) 2B + 4A = 2 x + 4 x

= +

=

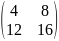
Questions:

A = B = C =

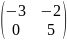
Calculate

1. A + C

2. A – C

3. 2B

4. 3C

5. 2B + 3C

6. 2B – 3C

7. 3A

8. B + 3A

Answers

1. A + C = +

=

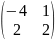
2. A – C = -

=

3. 2B = 2 x

=

4. 3C = 3 x

=

5. 2B + 3C = +

=

6. 2B – 3C = -

=

=

7. 3A = 3 x

=

8. B + 3A = +

=

Multiplying Matrices

In this course, for simplicity, we’ll only consider 2 x 2 (2 by 2) matrices under multiplication:

A = B =

Example: Find AB and BA

AB = A x B

=

We multiply the rows into the columns

=

=

BA =

=

=

So AB BA

Practice Questions

A = B = C =

Calculate:

1. AB

2. CA

3. 3A x C

4. A X 3C

5. 2B x 2C

6. 2B X 2A

Answers

1. AB =

=

=

2. CA =

=

=

3. 3A x C = 3 x

=

=

=

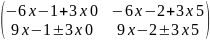
4. A x 3C = x 3

=

=

=

5. 2B x 2C = 2 x x 2 x

=

=

=

6. 2B x 2A = 2 x x 2 x

=

=

=