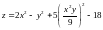Лекции, Гришин С.А. / Materialy_k_lektsii_Pervye_integraly
.docxМатериалы к лекции «Первые интегралы»
Система ДУ:
 (1)
(1)
Опр. Первым
интегралом системы (1) называют
функцию ,
сохраняющую постоянное значение по
,
сохраняющую постоянное значение по на
любом решении (1), проходящем через
точку
на
любом решении (1), проходящем через
точку .
.
Геометрический
смысл. Вся поверхность пространства
пространства заполнена
траекториями
заполнена
траекториями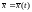 системы
(1).
системы
(1).
Постоянство значений первого интеграла системы (1) равносильно тому, что его полная производная
 (2)
(2)
Знание
первого интеграла системы (1) позволяет
понизить на единицу порядок исходной
системы ДУ. Например,
 –
первый интеграл системы (1), для которого
–
первый интеграл системы (1), для которого
 в
точке
в
точке .
Тогда уравнение
.
Тогда уравнение неявно
задает дифференцируемую функцию
неявно
задает дифференцируемую функцию и
с ее помощью можно исключит переменную
и
с ее помощью можно исключит переменную из
первых
из
первых уравнений
системы (1).
уравнений
системы (1).
Замечание
1. Если
первый
интеграл системы (1), то ее первым
интегралом является функция для
любой функции
для
любой функции .
.
Опр. Первые
интегралы называются
независимыми в области
называются
независимыми в области ,
если в каждой ее точке ранг матрицы
,
если в каждой ее точке ранг матрицы равен
равен .
.
Теорема 1. (о существовании первых интегралов)
В окрестности
любой точки
система
(1) имеет независимых
первых интегралов.
независимых
первых интегралов.
Док.
Пусть .
По теореме существования и единственности
для ДУ, существует
.
По теореме существования и единственности
для ДУ, существует
решение системы (1)
 ,
(3)
,
(3)
для которых .
Ранг матрицы
.
Ранг матрицы равен
равен ,
поскольку матрица единичная. Тогда по
теореме о неявной функции в окрестности
точки
существуют
дифференцируемые функции
,
поскольку матрица единичная. Тогда по
теореме о неявной функции в окрестности
точки
существуют
дифференцируемые функции ,
для которых
,
для которых
 (4)
(4)
Равенства (4) превращаются в тождества на любом решении (3) системы(1) с начальным условием .
Таким
образом, функции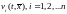 являются первыми интегралами системы
(1). Их независимость следует из того,
что матрица
являются первыми интегралами системы
(1). Их независимость следует из того,
что матрица в точке
единичная.
в точке
единичная.
Замечание 2. Если система (1) имеет независимых первых интегралов , то ее общее решение (3) неявно задается системой уравнений (4).
Замечание 3. Если система (1) автономная,
 (1)*
(1)*
а начальная
точка не
особая, например
не
особая, например ,
то система (1)* имеет
первых
интегралов в окрестности точки
.
Действительно, систему (1)* можно записать
в виде:
,
то система (1)* имеет
первых
интегралов в окрестности точки
.
Действительно, систему (1)* можно записать
в виде:
 (1)**
(1)**
и по теореме
1 у нее есть
независимых
первых интегралов принимающих
постоянные значения на решениях (1)**, а
значит и на (1)*. Таким образом, эти функции
являются первыми интегралами автономной
системы (!)*.
принимающих
постоянные значения на решениях (1)**, а
значит и на (1)*. Таким образом, эти функции
являются первыми интегралами автономной
системы (!)*.
Как находят первые интегралы ДУ?
Симметричная форма записи системы ДУ.
 (5)
(5)
Если ,
то в такой форме можно записать систему
(1).
,
то в такой форме можно записать систему
(1).
Пример 1
Решить систему

Система автономная, записана в симметричной форме. Один из ее первых интегралов легко увидеть:

Если решение
системы, то
решение
системы, то принимает
постоянное значение (производная по
в
силу системы равна нулю) и является ее
первым интегралом.
принимает
постоянное значение (производная по
в
силу системы равна нулю) и является ее
первым интегралом.
Для нахождения второго интеграла, перепишем симметричную форму в виде:

Общее
решение исходной системы при имеет
вид
имеет
вид .
.
На
плоскости решение
имеет вид:
решение
имеет вид:

Уравнения с частными производными первого порядка
Однородные уравнения.
Однородным линейным уравнением с частными производными первого порядка называют уравнение
 (6)
(6)
связывающее
частные производные первого порядка
неизвестной функции с
заданными функциями
с
заданными функциями класса
класса (коэффициентами
уравнения).
(коэффициентами
уравнения).
Теорема
2. Функция является
решением уравнения (6) в том и только в
том случае, если она является первым
интегралом системы
является
решением уравнения (6) в том и только в
том случае, если она является первым
интегралом системы
 (7)
(7)
Док.
Если
–
решение (6), то производная
 в
силу системы (7) равна нулю:
в
силу системы (7) равна нулю:

И функция постоянна на решениях системы (7), т.е. она первый интеграл этой системы.
Обратно,
 –
первый интеграл системы (7), тогда он
постоянен на решениях (7) и его полная
производная
–
первый интеграл системы (7), тогда он
постоянен на решениях (7) и его полная
производная и
и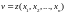 является
решением (6).
является
решением (6).
Теорема 3. (об структуре общего решения линейного уравнения)
Пусть независимые
первые интегралы системы (7) в окрестности
точки
независимые
первые интегралы системы (7) в окрестности
точки .
Тогда для любой функции
.
Тогда для любой функции функция
функция является
решением уравнения (6).
является
решением уравнения (6).
Док. По
теореме 2 любая из функций является
решением (6), поэтому ее производная в
силу систему (7)
является
решением (6), поэтому ее производная в
силу систему (7)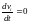 .
Тогда производная функции
в силу системы (7) равна
.
Тогда производная функции
в силу системы (7) равна и она является первым интегралом системы
(7), поэтому и решением (6).
и она является первым интегралом системы
(7), поэтому и решением (6).
В предположениях
теоремы верно и обратное утверждение:
для любого решения уравнения
(6) найдется такая функция
,
для которой
уравнения
(6) найдется такая функция
,
для которой
Пример 2.
Найти общее решение уравнения в
области
.
в
области
.
Решение.
Составим уравнение (7):

Первые интегралы системы:

Подставляем
в уравнение значение
значение :
: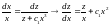
Решение линейного ДУ:

Исключаем :
:
Найденные два первых интеграла позволяют написать общее решения исходного уравнения в области .

для любой функции .
Неоднородные (квазилинейные) уравнения.
Рассмотрим уравнение с частными производными первого порядка вида:
 (8)
(8)
Здесь функции
класса
функции
класса ,
, ,
функция
,
функция –
решение (8).
–
решение (8).
С уравнением (8) связана система ДУ:
 (9)
(9)
Решения (9) называются характеристиками уравнения (8).
Теорема 4.
Любое
решение
уравнения
(8) задает в пространстве поверхность,
через каждую точку которой проходит
решение системы (9) и оно принадлежит
поверхности, т.е. поверхность состоит
из характеристик уравнения (8).
поверхность,
через каждую точку которой проходит
решение системы (9) и оно принадлежит
поверхности, т.е. поверхность состоит
из характеристик уравнения (8).
Док.
Пусть
кривая является
траекторий решения (9) и принадлежит
поверхности
является
траекторий решения (9) и принадлежит
поверхности с уравнением
с уравнением .
Ее касательный вектор
.
Ее касательный вектор перпендикулярен
нормали
перпендикулярен
нормали поверхности:
поверхности:

Таким образом, – решение уравнения (8)
Обратно,
–
решение уравнения (8). Оно задает
в поверхность
.
Покажем, что через каждую точку
поверхность
.
Покажем, что через каждую точку проходит
и единственная характеристика,
принадлежащая
.
Пусть
проходит
и единственная характеристика,
принадлежащая
.
Пусть –
проекция
–
проекция на
на .
Через точку
проходит
единственное решение системы ДУ:
.
Через точку
проходит
единственное решение системы ДУ:

Тогда
кривая лежит
на поверхности
для
всех
лежит
на поверхности
для
всех и
является характеристикой. Действительно,
и
является характеристикой. Действительно,

и является решением (9).
Теорема 5.
Пусть –первый
интеграл системы (9) в области
–первый
интеграл системы (9) в области и
в точке
и
в точке
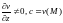 .
Тогда уравнение
.
Тогда уравнение задает
(неявно) решение (8) в окрестности точки
.
задает
(неявно) решение (8) в окрестности точки
.
Док. Из
условия первого интеграла системы (9):
системы (9):
 (*)
(*)
Заметим,
что по правилу дифференцирования неявных
функций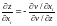 .
.
Тогда, разделив (*) на ,
получим
,
получим (8).
(8).
Теорема 6. (об общем решении квазилинейного уравнения)
Пусть –
независимые первые интегралы системы
(9). Функция
–
независимые первые интегралы системы
(9). Функция является
решением уравнения (8) в окрестности
точки
в
том и только в том случае, если она
удовлетворяет равенству
является
решением уравнения (8) в окрестности
точки
в
том и только в том случае, если она
удовлетворяет равенству

для любой
функции в
окрестности точки
.
в
окрестности точки
.
(без доказательства)
Пример 3.
Найти общее решение уравнения .
.
Решение.
 –
неизвестная функция,
–
неизвестная функция,
 .
Соответствующая ей система для
характеристик
.
Соответствующая ей система для
характеристик
 может быть записана в симметричной
форме
может быть записана в симметричной
форме
Найдем три ее первых интегралов.
А.

B.

C.

Общее решение задается неявно уравнением

при любой
функции .
.
Задача
Коши для квазилинейных уравнений
(8) ( )
)
Пусть в
пространстве задана
гладкая кривая
задана
гладкая кривая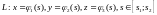 .
При решении задачи Коши требуется найти
решение
.
При решении задачи Коши требуется найти
решение уравнения
уравнения
 , (10)
, (10)
содержащее
кривую ,
т.е.
,
т.е.
Теорема 7. (существования решения задачи Коши)
Пусть в
каждой точке кривой
выполнено
условие .
Тогда существует решение задачи Коши
в некоторой окрестности любой точки
кривой
.
.
Тогда существует решение задачи Коши
в некоторой окрестности любой точки
кривой
.
Док.
Пусть –
произвольная точка кривой
.
Через нее проходит и единственное
решение системы (характеристика)
–
произвольная точка кривой
.
Через нее проходит и единственное
решение системы (характеристика)

Обозначим его через
 (11).
(11).
Параметрические уравнения (11) задают в пространстве поверхность , содержащую :
 –
координаты точки
–
координаты точки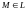 .
.
Покажем,
что условие
обеспечивает
возможность однозначно выразить через
через и
и .
.
Действительно,
условием обратимости системы в
окрестности точки
является:
в
окрестности точки
является:
 .
Таким образом, существуют гладкие
функции
.
Таким образом, существуют гладкие
функции ,
для которых
,
для которых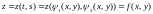 –
решение задачи Коши для уравнения (10).
–
решение задачи Коши для уравнения (10).
Пример 4. Решить задачу Коши для уравнения

с граничным
условием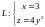 .
.
Решение
Система для характеристик:

Поиск первых интегралов ( ):
A.

B.
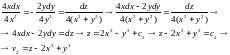
Общее решение уравнения задается в виде равенства

c произвольной
гладкой функцией .
Полагаем, что уравнение
.
Полагаем, что уравнение можно
разрешить в виде
можно
разрешить в виде с
некоторой гладкой функцией
с
некоторой гладкой функцией .
.
Условия на
границе:
Обозначение: