
Лекции, Гришин С.А. / Lektsia_na_temu_Ustoychivost
.docxЛекция на тему «Устойчивость по Ляпунову»
1. Основные определения.
А.
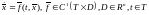 (1)
(1)
неавтономная
СДУ, автономная, если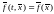 ;
;
B.
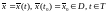 –
решение задачи Коши на промежутке
–
решение задачи Коши на промежутке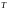 ;
;
C.
устойчивость по Ляпунову
частного решения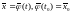 системы (1) при
системы (1) при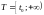 :
:
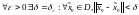 решение
решение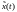 (1)
c начальным условием
(1)
c начальным условием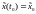 удовлетворяет
неравенству
удовлетворяет
неравенству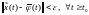 .
.
D. Асимптотическая устойчивость частного решения системы (1), :
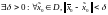 решение
(1)
c начальным условием
удовлетворяет
условию
решение
(1)
c начальным условием
удовлетворяет
условию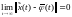 .
.
Замечание
1. Если частное решение устойчиво (или
неустойчиво) для начального момента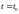 ,
то оно будет устойчивым (или неустойчивым)
для
,
то оно будет устойчивым (или неустойчивым)
для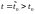 .
.
Замечание 2. Вопрос об устойчивости частного решения (1) всегда может быть сведен к устойчивости нулевого решения другой системы ДУ:
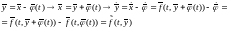
Пример 1.
Исследовать на устойчивость нулевое
решение уравнения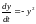 .
.
Найдем общее решение:
Для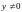 имеем
имеем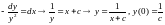 .
.
Если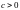 ,
то
,
то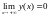 .
Если
.
Если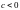 ,
то решение имеет вертикальную асимптоту
и становится как угодно большим при
любых как угодно малых
,
то решение имеет вертикальную асимптоту
и становится как угодно большим при
любых как угодно малых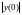 .
Итог: нулевое решение уравнения
неустойчиво.
.
Итог: нулевое решение уравнения
неустойчиво.
Пример 2.
Исследовать на устойчивость нулевое
решение системы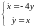
Решение
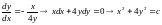
Решение
системы, проходящее через точку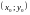 ,
неявно задается уравнением
,
неявно задается уравнением
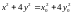 и
принадлежит эллипсу. Если начальные
условия
находятся
в эллипсе
и
принадлежит эллипсу. Если начальные
условия
находятся
в эллипсе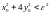 ,
то решение находится в круге
,
то решение находится в круге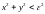 и нулевое решение устойчиво по Ляпунову,
но не асимптотически.
и нулевое решение устойчиво по Ляпунову,
но не асимптотически.
Рассмотрим условия, обеспечивающие устойчивость нулевого решения системы
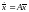 (2)
(2)
с постоянной
матрицей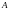 .
.
Теорема 1
Если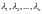 корни
характеристического многочлена
корни
характеристического многочлена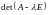 матрицы
,
то справедливы три утверждения:
матрицы
,
то справедливы три утверждения:
1. Если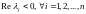 ,
то нулевое решение системы асимптотически
устойчиво.
,
то нулевое решение системы асимптотически
устойчиво.
2. Если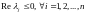 и
все корни
и
все корни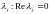 имеют
кратность 1, то нулевое решение системы
устойчиво по Ляпунову.
имеют
кратность 1, то нулевое решение системы
устойчиво по Ляпунову.
3. Если хотя бы один из корней имеет положительную действительную часть, то нулевое решение неустойчиво.
Док.
Из курса ДУ известна структура общего решения системы с постоянными коэффициентами:
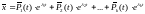 (*)
(*)
где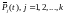 –
n –мерные вектора,
координаты которых многочлены переменной
–
n –мерные вектора,
координаты которых многочлены переменной ,
степень которых по крайней мере на
единицу меньше кратности корня
,
степень которых по крайней мере на
единицу меньше кратности корня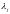 .
.
Если
,
то асимптотическую устойчивость нулевого
решения обеспечивает условие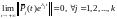 .
.
Если
и
корни с нулевой действительной частью
имеют кратность 1, то соответствующий
при экспоненте многочлен имеет нулевую
степень (константа) и близость к нулю
слагаемого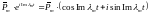 обеспечивается малым отклонением от
нуля начального условия.
обеспечивается малым отклонением от
нуля начального условия.
Если корень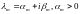 ,
то решение
,
то решение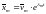 ,
где
,
где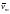 -
собственный вектор, соответствующий
-
собственный вектор, соответствующий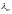 ,
неограниченно при больших
.
,
неограниченно при больших
.
Существует несколько алгебраических критериев выполнения условия 1. Теоремы 1.
Приведем один из них.
Критерий Рауса-Гурвица
Из коэффициентов характеристического уравнения
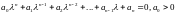
матрицы
системы (2) составляется квадратная
матрица порядка по
следующему принципу:
по
следующему принципу:
1. на главной
диагонали располагаются коэффициенты
от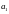 в
верхнем левом углу до
в
верхнем левом углу до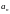 –
в нижнем правом;
–
в нижнем правом;
2. столбцы заполняются коэффициентами одинаковой четности индекса с диагональным элементом этого столбца. Если выходят из диапазона 0 - , ставятся нули;
3. вычисляются
главные миноры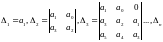
Условие 1. Теоремы 1 выполняется в том и только в том случае, если
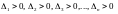 (3)
(3)
Пример 3. Исследовать на устойчивость нулевое решение уравнения
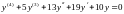
Решение.
Характеристическое
уравнение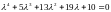
Матрица Рауса имеет вид:
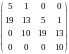
Ее главные миноры:
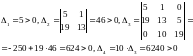
Действительные части всех собственных чисел отрицательные, поэтому нулевое решение асимптотически устойчиво.
Функции Ляпунова. Исследование на устойчивость с помощью функции Ляпунова
Производной
функции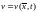 в
силу системы (1) называют выражение
в
силу системы (1) называют выражение
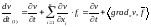 (3)
(3)
Оно совпадает
с производной по
функции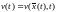 ,
где
,
где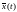 –
решение (1).
–
решение (1).
Функцию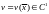 называют
функцией Ляпунова системы
(1), если существует окрестность
называют
функцией Ляпунова системы
(1), если существует окрестность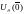 для
которой
для
которой
1.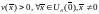 :
2.
:
2.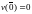 :
3.
:
3.
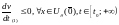
Теорема 2 (теорема Ляпунова об устойчивости)
Пусть
система (1) имеет нулевое решение: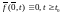 и в некоторой окрестности
у
нее существует функция Ляпунова. Тогда
нулевое решение устойчиво по Ляпунову.
и в некоторой окрестности
у
нее существует функция Ляпунова. Тогда
нулевое решение устойчиво по Ляпунову.
Док.

Возьмем
любое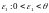 .
Через
.
Через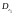 обозначим
ограниченную и замкнутую область
обозначим
ограниченную и замкнутую область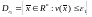 с
границей
с
границей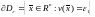 .
.
Обозначим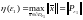 .
Здесь
.
Здесь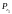 –
точка на границе
–
точка на границе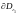 ,
наиболее удаленная от начала координат.
Покажем, что
,
наиболее удаленная от начала координат.
Покажем, что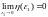 ,
т.е. с уменьшением
,
т.е. с уменьшением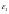 область
область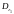 попадает
в любую наперед заданную окрестность
начала координат.
попадает
в любую наперед заданную окрестность
начала координат.
Предположим
противное. Тогда для некоторого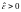 существует
последовательность
существует
последовательность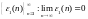 и
последовательность точек
и
последовательность точек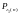 ,
для которых
,
для которых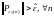 .
Последовательность точек
ограниченная,
поэтому по теореме Вейерштрасса у нее
существует сходящаяся подпоследовательность
.
Последовательность точек
ограниченная,
поэтому по теореме Вейерштрасса у нее
существует сходящаяся подпоследовательность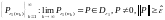 .
Тогда из непрерывности функции Ляпунова
.
Тогда из непрерывности функции Ляпунова
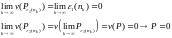
Полученное противоречие доказывает первое утверждение: .
Второе
утверждение: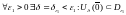
Оно следует
из непрерывности функции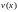 и
условия
и
условия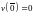 .
Действительно,
.
Действительно,
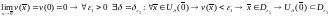
Третье
утверждение: решение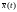 системы
(1) с начальным значением
системы
(1) с начальным значением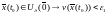 принадлежит
для
всех
принадлежит
для
всех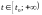 ,
т.е. если в начальный момент времени
решение находилось достаточно близко
к нулю, то при
,
т.е. если в начальный момент времени
решение находилось достаточно близко
к нулю, то при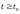 оно
не может покинуть границ области
.
оно
не может покинуть границ области
.
Предположим,
что это не так: существует момент
времени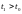 ,
для которого
,
для которого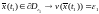 .
Применим теорему Лагранжа к функции
.
Применим теорему Лагранжа к функции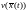 на
отрезке
на
отрезке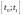 :
:
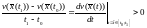
Здесь числитель и знаменатель дроби в левой части равенства положительный:
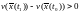 т.к.
т.к.
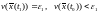 .
Последнее неравенство противоречит
отрицательности производной функции
Ляпунова в силу системы (1).
.
Последнее неравенство противоречит
отрицательности производной функции
Ляпунова в силу системы (1).
Объединяем все три доказанных утверждения, для проверки определения устойчивости решения по Ляпунову:
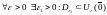 (Первое утверждение)
(Первое утверждение)
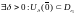 (Второе утверждение)
(Второе утверждение)
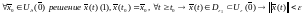
(Третье утверждение)
Теорема 3 (об асимптотической устойчивости)
Пусть
система (1) имеет нулевое решение:
и у нее существует функция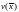 Ляпунова, для которой в некоторой
окрестности
выполняется
неравенство
Ляпунова, для которой в некоторой
окрестности
выполняется
неравенство
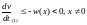 с
некоторой непрерывной функцией
с
некоторой непрерывной функцией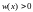 .
Тогда нулевое решение системы (1)
асимптотически устойчиво.
.
Тогда нулевое решение системы (1)
асимптотически устойчиво.
Док.
В условиях
теоремы нулевое решение устойчиво по
Ляпунову: для любого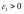 существует
существует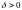 для
которого решение
системы
(1) с начальным условием
для
которого решение
системы
(1) с начальным условием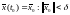 принадлежит
принадлежит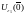 при
всех
при
всех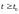 .
Нужно доказать, что
.
Нужно доказать, что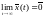 .
.
Предположим
противное: существует число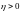 и
последовательность моментов времени
и
последовательность моментов времени
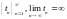 ,
для которых
,
для которых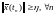 .
.
Рассмотрим
последовательность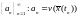 и
число
и
число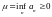 .
Докажем, что в нашем предположении
.
Докажем, что в нашем предположении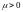 (первое утверждение).
Действительно, если бы
(первое утверждение).
Действительно, если бы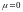 ,
то существовала бы подпоследовательности
,
то существовала бы подпоследовательности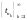 и
и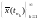 ,
для которых
,
для которых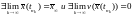 .
.
В нашем
предположении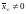 ,
но тогда из непрерывности функции
Ляпунова и условия
имеем:
,
но тогда из непрерывности функции
Ляпунова и условия
имеем:
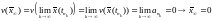
Утверждение
1 доказано и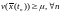
Докажем,
что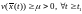 (второе утверждение)
(второе утверждение)
Действительно,
на любом отрезке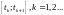 функция
монотонно
убывает, поскольку
функция
монотонно
убывает, поскольку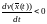 ,
и поэтому
,
и поэтому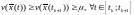
Существует
число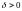 ,
для которого
,
для которого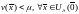 (третье утверждение)
(третье утверждение)
Это следует из непрерывности функции Ляпунова и условия :
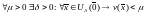
Поэтому
решение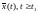 системы (1) находится в шаре
и не бывает в шаре
системы (1) находится в шаре
и не бывает в шаре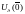 ,
поэтому находится в области
,
поэтому находится в области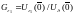 .
Пусть
.
Пусть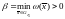 .
Тогда для
.
Тогда для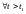 справедливо неравенство, которое
является следствием предположения о
том, что
справедливо неравенство, которое
является следствием предположения о
том, что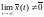
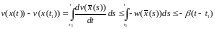
Последнее неравенство при больших становится неверным, поскольку приводит к отрицательным значениям функции Ляпунова. Следовательно, .
Как строить функции Ляпунова конкретных систем?
Пример 4.
Исследовать на устойчивость нулевое
решение уравнения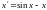 .
.
Решение
Рассмотрим
функцию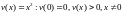 .
Ее производная в силу уравнения:
.
Ее производная в силу уравнения:
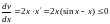
Действительно,
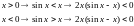 .
По теореме 2 нулевое решение устойчиво
по Ляпунову.
.
По теореме 2 нулевое решение устойчиво
по Ляпунову.
На самом деле устойчивость нулевого решения асимптотическая:
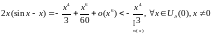
Пример 5.
Исследовать на устойчивость нулевое
решение системы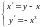 .
.
Решение.
Линейным
приближением к данной системе является
система с матрицей
с матрицей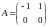 .
Ее характеристический многочлен
.
Ее характеристический многочлен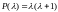 имеет
корни
имеет
корни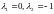 .
.
Собственные
вектора, соответствующие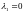 ,
лежат на прямой
,
лежат на прямой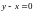 ,
а собственные вектора с
,
а собственные вектора с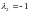 лежат
на прямой с уравнением
лежат
на прямой с уравнением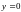 (ось абсцисс). Попытаемся найти функцию
Ляпунова в виде суммы квадратов отклонений
от этих сепаратрисс. Первые два
условия
(ось абсцисс). Попытаемся найти функцию
Ляпунова в виде суммы квадратов отклонений
от этих сепаратрисс. Первые два
условия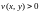 и
и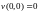 выполнены.
Проверим третье:
выполнены.
Проверим третье:
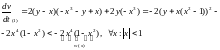
Условие теоремы 2 выполнены. Нулевое решение асимптотически устойчиво.
Следующая теорема подробнее рассматривает случай нулевого значения производной функции Ляпунова в силу системы.
Теорема 4 (Красовский) (без доказательства)
Пусть
система (1) имеет нулевое решение:
и в некоторой окрестности
у
нее существует функция Ляпунова
,
для которой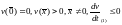 .
Множество
.
Множество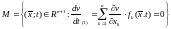 не
содержит целых траекторий, кроме
не
содержит целых траекторий, кроме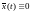 , не
существует решения
, не
существует решения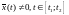 системы
(1) принадлежащее
системы
(1) принадлежащее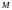 .
Тогда нулевое решение системы (1)
асимптотически устойчиво.
.
Тогда нулевое решение системы (1)
асимптотически устойчиво.
Еще одно теорема указывает достаточные условия неустойчивости нулевого решения
Теорема 5 (о неустойчивости) (без доказательства)
Пусть для автономной системы
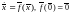 (1а)
(1а)
имеется
функция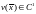 ,
определенная в некоторой окрестности
,
определенная в некоторой окрестности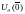 ,
для которой производная
,
для которой производная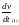 в силу системы положительно определена
(
в силу системы положительно определена
(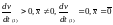 ).
Существует последовательность
).
Существует последовательность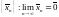 ,
для которой
,
для которой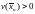 .
Тогда нулевое решение системы неустойчиво.
.
Тогда нулевое решение системы неустойчиво.
Пример 6.
Исследовать на устойчивость нулевое
решение системы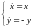 .
.
Решение
Функция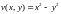 удовлетворяет
условию теоремы 5:
удовлетворяет
условию теоремы 5:
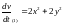 –
положительно определена в любой
окрестности начала координат;
–
положительно определена в любой
окрестности начала координат;
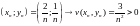
В неустойчивости
нулевого решения можно убедится
непосредственно, находя общее решение
системы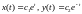 ,
которое покидает любую окрестность
начала координат при
,
которое покидает любую окрестность
начала координат при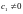 и
и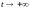 .
.
Устойчивость по первому приближению
Рассмотрим
систему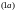
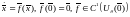
Разложим
функцию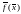 в
окрестности точки
в
окрестности точки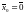 по
формуле Маклорена:
по
формуле Маклорена:
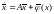 (1в)
(1в)
г де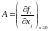 –
матрица первого приближения,
–
матрица первого приближения,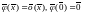 при
при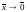 - остаточный член.
- остаточный член.
Функция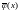 называется
возмущением системы
называется
возмущением системы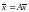 с
постоянной матрицей, если она имеет
малую норму (допускаются возмущения
с
постоянной матрицей, если она имеет
малую норму (допускаются возмущения ,
зависящие явно от
,
и малые на полуоси
)
,
зависящие явно от
,
и малые на полуоси
)
Опр. Линейная
система
называется
устойчивой по первому
приближению, если устойчиво нулевое
решение системы (1в) для любого возмущения
с
достаточно малым значением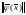 .
.
Теорема 7. (об устойчивости по первому приближению)
Пусть для
возмущенной системы вида
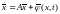 выполнены
условия:
выполнены
условия:
1. все
характеристические числа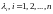 матрицы
имеют
отрицательные действительные части;
матрицы
имеют
отрицательные действительные части;
2.
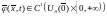 ,
, 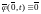
3. справедлива
оценка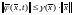 с
функцией
с
функцией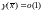 при
.
при
.
Тогда нулевое решение возмущенной системы асимптотически устойчиво.
Док.
Пусть
числа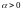 и
таковы,
что
и
таковы,
что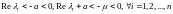 .
.
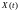 –
Фундаментальная матрица системы (2),
столбцами которой являются ее решения
с начальными условиями
–
Фундаментальная матрица системы (2),
столбцами которой являются ее решения
с начальными условиями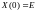 –
единичная матрица.
–
единичная матрица.
Норма
каждого из решений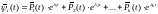 оценивается:
оценивается:
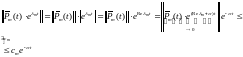
Отсюда
следует существование константы ,
для которой
,
для которой
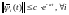 .
(**)
.
(**)
Рассмотрим
функцию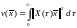 .
Заметим, что
.
Заметим, что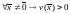 и
и
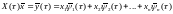 – решение невозмущенной системы (2) с
начальным условием
– решение невозмущенной системы (2) с
начальным условием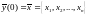
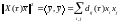 ,
где
,
где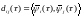
С учетом (**) справедлива оценка:
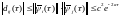 (***)
(***)
Тогда функцию можно представить в виде квадратичной формы:
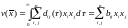 ,
,
где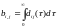 (оценка (***) обеспечивает сходимость
интегралов).
(оценка (***) обеспечивает сходимость
интегралов).
Вычислим
производную функции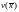 сначала
в силу невозмущенной системы:
сначала
в силу невозмущенной системы:
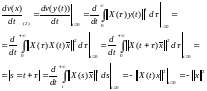
Вычислим производную функции в силу возмущенной системы:
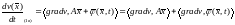
Первое
слагаемое в этой сумме – производная
функции
в
силу невозмущенной системы. Оценим
второе слагаемое с использованием
неравенства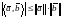 и
ограниченности
и
ограниченности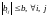 коэффициентов
квадратичной формы:
коэффициентов
квадратичной формы:
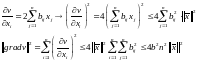
С учетом оценки возмущения, имеем
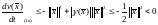
в достаточно малой окрестности начала координат. Тогда по теореме (2) нулевое решение возмущенной системы устойчиво.
Замечание. Если хотя бы один из корней характеристического многочлена матрицы линейного приближения имеет положительную действительную часть, то нулевое решение возмущенной системы неустойчиво.
Пример 8.
При каких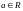 нулевое
решение системы
нулевое
решение системы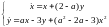 асимптотически
устойчиво.
асимптотически
устойчиво.
Решение
Матрица
линейного приближения: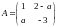
Характеристический
многочлен: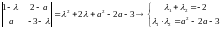
Исследование знаков корней:
Случай 1.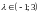
Корни разных знаков, нулевое решение неустойчиво;
Случай 2.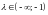
Корни одного знака и отрицательные, нулевое решение асимптотически устойчиво.
Случай 3.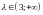
Корни одного знака и положительные, нулевое решение неустойчиво.
Случай
4.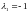 или
или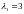
Характеристический
многочлен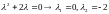 и
система линейная. По теореме 1 нулевое
решение устойчиво, но не асимптотически.
и
система линейная. По теореме 1 нулевое
решение устойчиво, но не асимптотически.
Классификация особых точек линейных систем на плоскости.
Рассматриваются линейные системы ДУ на плоскости:
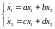 (4)
(4)
Случай 1.
Собственные числа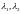 матрицы
матрицы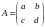 действительные, различные и одного
знака.
действительные, различные и одного
знака.
Имеются
два собственных вектора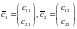 с
собственными числами
соответственно
и невырожденная матрица
с
собственными числами
соответственно
и невырожденная матрица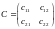 .
Линейное преобразование
.
Линейное преобразование приводит
(4) к диагональному виду
приводит
(4) к диагональному виду
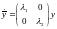 (5)
(5)
Действительно,
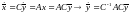
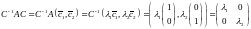
Решения
системы (5)
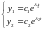 лежат
на траекториях
лежат
на траекториях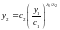 ,
изображенных на рис
,
изображенных на рис
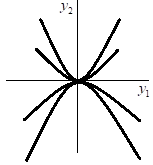
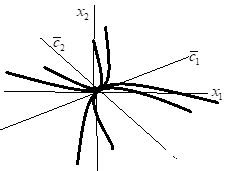
Рис 1 Узел Рис 1.1
При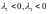 нулевое решение асимптотически устойчиво
(устойчивый узел). При
нулевое решение асимптотически устойчиво
(устойчивый узел). При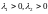 решение
неустойчиво (неустойчивый узел). При
обратном преобразовании на плоскость
решение
неустойчиво (неустойчивый узел). При
обратном преобразовании на плоскость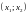 картинка
подвергнется преобразованию подобия
по осям координат, повороту относительно
начала координат без параллельного
переноса (рис 1.1)
картинка
подвергнется преобразованию подобия
по осям координат, повороту относительно
начала координат без параллельного
переноса (рис 1.1)
Случай 2. Собственные числа матрицы действительные, различные и разных знаков.
