Лекции, Гришин С.А. / Lektsia_DIU-14_Kraevye_zadachi

Лекция ДИУ 14. Краевая задача, задача Штурма-Лиувилля

Краевой задачей для линейного ДУ второго порядка вида

(1)

называют нахождение функции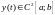 – решения уравнения (1), удовлетворяющего краевым условиям типа:

Краевая задача называется однородной и регулярной, если

.

К виду (1) приводятся любые линейные ДУ второго порядка путем умножения правой и левой частей уравнения на специально подобранную положительную функцию (разберите на семинаре).

Пусть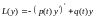 – линейный дифференциальный оператор, действующий из в , определенный на функциях , удовлетворяющих граничным условиям . Область определения оператора представляет собой всюду плотное множество в пространстве . В лекции будут рассматриваться условия, при которых область значений оператора содержит пространство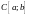 – существование решения краевой задачи для любых непрерывных функций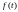 – а также условий, обеспечивающих единственность такого решения.

В операторной форме однородную и регулярную краевую задачу будем записывать так

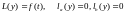(2)

Во-первых, изучим спектральные свойства оператора .

Задача Штурма-Лиувилля:

Найти числа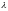 , при которых уравнение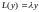 имеет ненулевые решения на отрезке 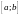, удовлетворяющие однородным граничным условиям .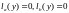

Изучение свойств собственных чисел оператора (решений задачи Ш-Л) и соответствующих им собственных функций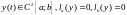 будет происходить путем построения интегрального оператора Фредгольма с симметричным ядром, собственные числа и собственные функции которого совпадают с решениями задачи Ш-Л и ненулевыми решениями уравнения .

Ядром такого оператора является функция Грина , определенная на квадрате .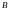

Функцией Грина однородной и регулярной краевой задачи (2) называют функцию , удовлетворяющую четырем условиям:

1. ;

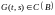2. фиксированного числа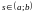 функция по переменной является решением однородного уравнения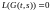 на каждом из интервалов и ;

3. Частная производная в точке терпит разрыв первого рода (скачок), причем

;

4. фиксированного числа функция удовлетворяет краевым условиям

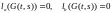
Теорема 1. Для регулярной краевой задачи (2), для которой однородное уравнени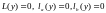е имеет только нулевое решение, существует и единственная функция Грина , симметричная, т.е. 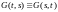на .

Док.

Пусть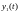 и – два решения задачи Коши уравнения с начальными условиями и соответственно. Решения и ненулевые, линейно независимые и удовлетворяют краевому условию . Первое следует из условия регулярности . Второе, в противном случае . Тогда

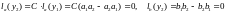
И, по условию теоремы, решение , что противоречит регулярности. Таким образом, и – фундаментальная система решений уравнения .

Рассмотрим функцию, определенную на квадрате :

Здесь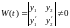 – определитель Вронского фундаментальной системы решений и .

Проверим, что является функцией Грина краевой задачи.

1. Непрерывность на квадрате следует из непрерывности решений и на отрезке ;

2. При фиксированном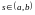

3.

Пояснение из курса ДУ.

Определитель Вронского фундаментальной системы решений уравнения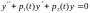 удовлетворяет дифференциальному уравнению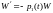 . Для оператора, записанного в форме (2)

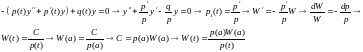
4.

Пусть уравнение имеет две функции Грина и .Тогда функция их разности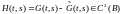 при любом фиксированном удовлетворяет по переменной уравнению на всем отрезке и краевым условиям

,

что, по условию теоремы, означает .

Пояснение:

1. Непрерывность в точке следует из условия 3 на функцию Грина.

2. Поскольку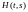 при фиксированном удовлетворяет уравнению , то

и вторая производная также непрерывная.

Пример 1. Построить функцию Грина краевой задачи

Решение

Решаем уравнение

Непрерывность:

Скачок производной:

Функция Грина: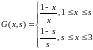

Следующая теорема устанавливает условия существования и единственности решения краевой задачи (1).

Теорема 2. (Гильберт)

Регулярная краевая задача (2) имеет решение для любой функции и оно единственное, если однородная краевая задача имеет только нулевое решение.

Док.

В условия теоремы существует и единственная функция Грина. Покажем, что функция

(3)

является решением краевой задачи (2).

Запишем функцию Грина в более симметричной форме:

, где – фундаментальная система решений, участвующая в построении функции Грина в теореме (1). Тогда

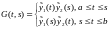
Проверим, что (3) удовлетворяет уравнению :

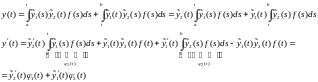
Заметим, что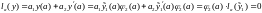

Аналогично устанавливается выполнение краевого условия на правом конце отрезка:

Продолжим дифференцирование:

Осталось доказать единственность решения краевой задачи (2).

Если решений два , определяемое формулой (3), и . Тогда их разность является решением однородного уравнения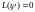 и удовлетворяет краевым условиям . Но тогда по условию теоремы .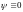

Вернемся к задаче Ш-Л и свойствам собственных чисел и собственных функций оператора

(4)

Теорема 3. (об эквивалентности)

Пусть краевая задача (2) для оператора регулярная, а уравнение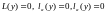 имеет только нулевое решение. Если – собственное число задачи Ш-Л и соответствующая ему собственная функция оператора , то – характеристическое число интегрального оператора

(5)

а – его характеристическая функция и наоборот. Здесь – функция Грина оператора

Док.

Пусть – собственная функция дифференциального оператора с собственным числом . Тогда по теореме 2 (Гильберт)

,

т.е. – характеристическое число, а – собственная функция интегрального оператора.

Обратно, пусть – характеристическое число, а – собственная функция интегрального оператора

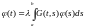
По способу построения функции Грина, интеграл можно дважды дифференцировать по переменной и по теореме 2 (Гильберт) функция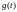 является решением краевой задачи

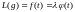с выполнением краевых условий . Поскольку , характеристическое число и собственная функция интегрального оператора являются собственным числом и собственной функцией дифференциального оператора с соблюдением краевых условий:

Свойства собственных чисел и собственных функций задачи Ш-Л.

1. Собственные функции задачи Ш-Л принадлежат пространству ;

2. Собственные числа задачи Ш-Л совпадают с характеристическими числами интегрального, самосопряженного, с непрерывным симметричным ядром – функцией Грина дифференциального оператора ;

3. Собственные числа задачи Ш-Л вещественные;

4. Собственные числа задачи Ш-Л простые (нет кратных);

Предположим обратное: существуют две линейно независимые собственные функции с одним собственным числом .Тогда их определитель Вронского

Выполнение для них краевых условий

Приводит к системе однородных уравнений с ненулевым определителем, т.е.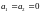 . Последнее противоречит условию регулярности: .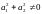

5. Собственные числа задачи Ш-Л образуют счетное множество и могут быть упорядочены по модулю

При этом .

Если бы число характеристических чисел интегрального оператора было бы конечным, то его ядро можно было представить в виде:

Тогда функция Грина была бы класса , что противоречит ее определению (разрыв первых производных на диагонали квадрата). Поэтому интегральный оператор, а значит и соответствующий ему дифференциальный, имеет счетное число характеристических чисел. Когда мы изучали общую теорию самосопряженных операторов, то отмечали сходимость ряда

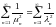
Что невозможно, если общий член ряда не стремится к нулю, т.е.

6. Собственные функции в задаче Ш-Л ортогональны.

Завершим тему формулировкой

Теорема 4. (Ляпунова)

Пусть удовлетворяет краевым условиям . Тогда раскладывается в ряд Фурье по ОНС собственных функций задачи Ш-Л

(6)

Здесь – последовательность всех собственных функций задачи Ш-Л, упорядоченных, например, по возрастанию модулей собственных чисел задачи Ш-Л.