Лекции, Гришин С.А. / Lektsia_DIU-13_Simmetrichnye_yadra
.docxЛекция ДИУ-13
Рассмотрим
какие возможности для поиска решения
дает предположение о симметрии
ядра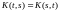
интегрального
уравнения Фредгольма
(1)
Как уже было установлено:
1. решение
есть и единственное при малых значениях
параметра
;
2. справедлива альтернатива Фредгольма в упрощенном варианте: либо неоднородное уравнение имеет единственное решение, либо однородное имеет ненулевые решения;
3. спектр действительный и не более, чем счетный;
4. имеется ОНС из собственных функций оператора, включая случай кратных корней.
В этой
лекции будет предпринята попытка
нахождения решения уравнения (1) через
собственные функции и характеристические
числа интегрального оператора с ядром
.
Сформулируем дополнительно утверждение, которое будет в дальнейшем использовано.
Теорема 1 (Гильберта-Шмидта) (без доказательства)
Если
функция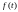
представима
в виде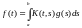
для
некоторой функции
,
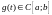то она раскладывается в абсолютно и
равномерно сходящийся ряд Фурье по ОНС
собственных функций
ядра
:
(2)
Здесь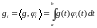
.
Теорема 2.
Пусть
–
ОНС собственных функций симметричного
ядра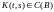
и
–
последовательность соответствующих
им характеристических чисел, возможно
кратных. Если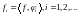
–
коэффициенты разложения свободного
члена
в
ряд Фурье по ОНС
,
число
не
является характеристическим числом
ядра оператора, то уравнение (1) имеет
единственное решение, представляемое
суммой абсолютно и равномерно сходящегося
ряда:
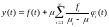(2)
Док.
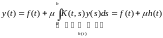
По теореме
Г-Ш функция
разлагается
в абсолютно и равномерно на
сходящийся
ряд Фурье по ОНС собственных функций
ядра
:
Вычислим
коэффициенты
:
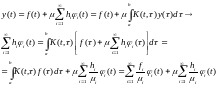
Сравнивая
коэффициентов справ и слева, получим
Подставляем полученное в выражение для решения:
Формулу (2) назовем первой формулой Шмидта.
Теорема 3.
Пусть
–
ОНС собственных функций симметричного
ядра
и
–
последовательность соответствующих
им характеристических чисел, возможно
кратных. Число
является характеристическим числом
ядра оператора кратности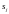
.
Свободный член
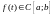ортогонален
собственным функциям
c
номерами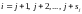
,
–
коэффициенты разложения свободного
члена
в
ряд Фурье по ОНС
(
).
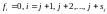Тогда уравнение (1) имеет бесконечное
множество решений, имеющее вид:
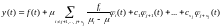(3)
с произвольными
константами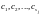
.
Док.
Подобно тому, как это делалось в доказательстве теоремы 2, ищем решение уравнения (1) в форме
,
что приводило к соотношению между
вида (*):
.
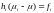Если
,
то коэффициенты
вычисляются из (*) по прежним формулам:
.
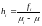Если
,
то соотношение (*) разрешимо только в
случае, когда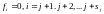
.
В этом случае, коэффициенты
произвольны.
Формула (3) называется второй формулой Шмидта.
Пример
1.Исследовать разрешимость интегрального
уравнения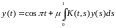
с
симметричным ядром
в
зависимости от значений параметра
.
Решение
Находим характеристические функции и соответствующие им собственные функции:
Заметим, что
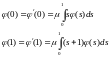(4)
Продолжим дифференцирование:
(5)
Случай
1.
,
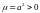Общее решение уравнения (5):
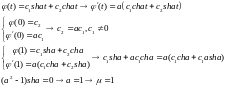
Собственные
функции: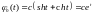
Случай 2.
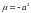
Общее решение уравнения (5):
Собственные
функции: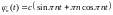
Нормировка:
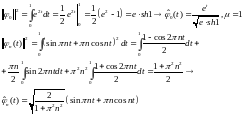
Коэффициенты Фурье функции :
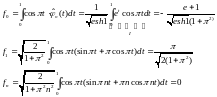
Если
,
то решение единственное и имеет вид:
Если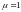
,
то уравнение не имеет решений поскольку
.
Если
,
то уравнение не имеет решений, поскольку
.
Если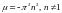
,
то решений бесконечно много, и они имеют
вид:
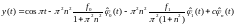
Наконец, сформулируем утверждение, доказанное нами для симметричного ядра, верное для любых непрерывных ядер. Оно называется альтернативой Фредгольма.
Для интегрального уравнения
с непрерывным
ядром на квадрате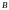
справедливо
одно из двух утверждений:
1. если не является характеристическим числом оператора Фредгольма, соответствующего уравнению (1), то уравнение всегда имеет единственное решение для любой непрерывной на функции . При этом уравнение
,
соответствующее сопряженному оператору, также имеет единственное решение. В этом случае однородные уравнения
,
имеют только нулевые решения.
2. Если является характеристическим числом уравнения (1), то оно является характеристическим числом сопряженного уравнения. Уравнение (1) разрешимо в том и только в том случае, если ортогональна собственным функциям сопряженного уравнения с характеристическим числом .
В случае 2. общее решение уравнения (1) является суммой частного решения уравнения (1) и общего решения сопряженного однородного уравнения и характеристическим числом .