Лекции, Гришин С.А. / Lektsia_DIU-12_Rezolventa_iterirovannye_yadra

Лекция ДИУ- 12

1. Степени оператора Фредгольма, итерированные ядра, резольвента оператора.

Рассмотрим еще одну форму представления решения интегрального уравнения Фредгольма

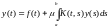(1)

с непрерывным на квадрате ядром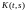 и свободным членом .

В операторной форме уравнение (1) запишется в виде: с оператором Фредгольма

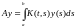(2)

Докажем, что степени оператора также являются интегральными операторами с непрерывными ядрами.

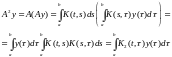
Ядро оператора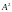 обозначено через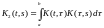 . Для удобства полагаем . Аналогично,

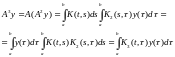
Здесь .

Для произвольного :

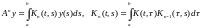(3)

Последовательность непрерывных на функций 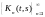называют последовательностью итерированных ядер. Если – характеристическое число оператора , то – характеристическое число оператора .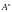

В представлении решения (1) методом последовательных приближений была построена последовательность функций , равномерный предел которой был решением уравнения (1). Представим эту последовательность с помощью итерированных ядер:

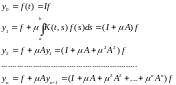
Оператор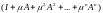 интегральный с ядром

Ряд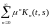 , как было установлена для последовательностей, равномерно сходится на при достаточно малых для уравнений Фредгольма и при любых для уравнений Вольтерра. Обозначим через . Тогда решение уравнения (1) может быть представлено в виде:

(4)

Функцию называют разрешающим ядром оператора Фредгольма или его резольвентой.

Пример 1. С помощью итерационных ядер найти резольвенту ядра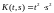 на квадрате .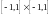

Решение

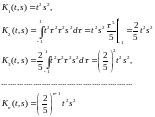
Подставляем полученное в ряд для резольвенты:

Сходимость ряда к резольвенте обеспечена по крайней мере для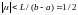 . На самом деле, ряд сходится при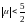

Пример 2. Построить резольвенту оператора и ее помощью решить уравнение

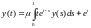при .

Решение.

Строим последовательность итерированных ядер:

Ряд для резольвенты:

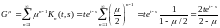
Формально, ряд геометрической прогрессии сходится при , но резольвента существует при .

Нахождение решения:

Проверка. Необходимо подставить найденную функцию в уравнение:

2. Степени оператора Вольтерра, итерирующие ядра, резольвента.

Оператор Вольтерра действует из пространства имеет вид:

.

Здесь – непрерывное ядро на треугольнике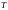 . Вся конструкция построения последовательности итерированных ядер для операторов Вольтерра наследуется от операторов Фредгольма, частным случаем которых они являются. Эта последовательность определяется рекуррентным соотношением (формально 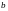заменяется на , – на )

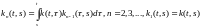
Степени оператора также являются интегральными операторами Вольтерра с ядром :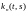

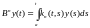
Последовательность функций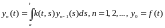 , как было доказано, равномерно на сходится к решению уравнения

при любых . Эта последовательность выражается через степени оператора (с заменой буквы на букву )

Оператор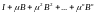 – интегральный оператор Вольтерра с ядром

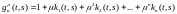
Тогда ряд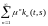 равномерно сходится на и

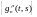Обе последовательности и равномерно сходятся: первая на отрезке , вторая – на треугольнике . Предельный переход при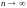 под знаком интеграла в этом случае возможен при любом .

(5)

Здесь функция называется резольвентой оператора Вольтерра (ср. с (4)).

Пример 3. Найти резольвенту оператора Вольтерра на отрезке с ядром .

Решение

Последовательность итерированных ядер:

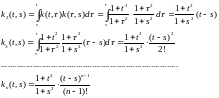
Нахождение резольвенты

Пример 4. Найти резольвенту оператора Вольтерра и с ее помощью решить интегральное уравнение

,

Решение

Находим итерированные ядра:

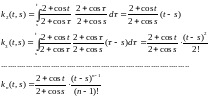
Находим резольвенту ( ):

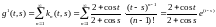
Решение интегрального уравнения: