
Лекции, Гришин С.А. / Lektsia_DIU-11_int_uravnenia
.docxЛекция ДИУ – 11, Классификация интегральных уравнений
Интегральное уравнение вида
 (1)
(1)
называется
уравнением Фредгольма второго рода.
Здесь –
непрерывное на квадрате
–
непрерывное на квадрате ядро,
ядро, – свободный член,
– свободный член, – параметр.
– параметр.
 -
решение уравнения. В случае
-
решение уравнения. В случае уравнение называется однородным.
уравнение называется однородным.
 (2)
(2)
Множество
решений уравнения (2) при фиксированном является
линейным пространством. Если оно не
нулевое, то
называется
характеристическим числом пространства,
элементы пространства – собственными
функциями, а его размерность
является
линейным пространством. Если оно не
нулевое, то
называется
характеристическим числом пространства,
элементы пространства – собственными
функциями, а его размерность – кратностью характеристического
значения
.
Если
конечное
число, то существует базис пространства
собственных функций
– кратностью характеристического
значения
.
Если
конечное
число, то существует базис пространства
собственных функций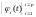 (возможно ортонормированный), по которому
раскладывается любая собственная
функция
(возможно ортонормированный), по которому
раскладывается любая собственная
функция :
:
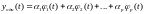 (3)
(3)
Если одно
из решений неоднородного уравнения
(1), то его общее решение
одно
из решений неоднородного уравнения
(1), то его общее решение имеет вид:
имеет вид:
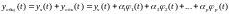 (4)
(4)
c произвольными
(вообще комплексными) константами .
.
Уравнение Фредгольма с вырожденным ядром.
Если ядро в уравнении (1) имеет вид

c функциями .
Оно называется вырожденным. Без
ограничения общности, можно предполагать
линейную независимость систем функций
.
Оно называется вырожденным. Без
ограничения общности, можно предполагать
линейную независимость систем функций и
и .
.
В случае,
когда
решение (1), после его подстановки в
уравнение и интегрирования тождества
на ,
получим:
,
получим:
 ,
где
,
где (5)
(5)
Умножим
правую и левую части равенства на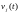 и
проинтегрируем полученное по
и
проинтегрируем полученное по на
отрезке
:
на
отрезке
:
 (6)
(6)
Здесь .
.
Система
уравнений (6) с неизвестными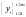 линейная
и ей можно придать матричную форму:
линейная
и ей можно придать матричную форму:
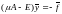 (7)
(7)
Здесь –
матрица,
–
матрица,
 –
столбец свободных членов,
–
столбец свободных членов, –
столбец неизвестных. Таким образом, для
уравнения (1) с вырожденным ядром
существование у него решения приводит
к существованию решения системы (7) и
наоборот. Если система (7) имеет решение
,
то оно, подставленное в (5), дает решение
(1). Вопрос о разрешимости линейной
системы изучен вами в курсе линейной
алгебры.
–
столбец неизвестных. Таким образом, для
уравнения (1) с вырожденным ядром
существование у него решения приводит
к существованию решения системы (7) и
наоборот. Если система (7) имеет решение
,
то оно, подставленное в (5), дает решение
(1). Вопрос о разрешимости линейной
системы изучен вами в курсе линейной
алгебры.
1. Если
однородная система имеет только нулевое решение (
не
является характеристическим число
матрицы), то неоднородная система (7)
имеет единственное решение, а значит и
интегральное уравнение также имеет
единственное решение.
имеет только нулевое решение (
не
является характеристическим число
матрицы), то неоднородная система (7)
имеет единственное решение, а значит и
интегральное уравнение также имеет
единственное решение.
2. Если
пространство решений однородной системы
имеет размерность (
является
характеристическим числом матрицы и
оператора), существует базис решений
однородной системы
(
является
характеристическим числом матрицы и
оператора), существует базис решений
однородной системы ,
который по формулам (5) породит базис
пространства решений однородного
интегрального уравнения.
,
который по формулам (5) породит базис
пространства решений однородного
интегрального уравнения.
3. Если в
условиях пункта 2 неоднородная система
(7) имеет решение ,
то интегральное уравнение имеет
бесконечное число решений, определяемых
формулой (4):
,
то интегральное уравнение имеет
бесконечное число решений, определяемых
формулой (4):
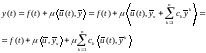
Диагональ
квадрата делит
его на два треугольника
делит
его на два треугольника и
и
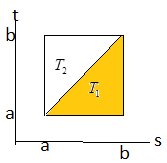
Рассмотрим
ядра интегральных уравнений такие,
что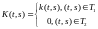 с
функцией
с
функцией непрерывной
на треугольнике
непрерывной
на треугольнике .
Тогда уравнение (1) с таким ядром примет
вид:
.
Тогда уравнение (1) с таким ядром примет
вид:
 (8)
(8)
Такие уравнения называются интегральными уравнениями Вольтерра второго рода. Уравнения Вольтерра являются частным случаем уравнений Фредгольма с непрерывным ядром. Следующие утверждения верны для уравнений обоих типов, если это не оговорено отдельно.
Пример.
Решить интегральное уравнение .
.
Решение

Здесь

Подставляя полученные значения интегралов в СЛУ, получим

Окончательно,
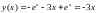
Общая теория интегральных уравнений с непрерывными ядрами.
Теорема 1 (единственности решения)
Для того, чтобы уравнения (1), (8) имели единственное решение необходимо и достаточно, чтобы их однородные уравнения ( ) имели только нулевое решение.
Док.
Это утверждение было нами доказано для уравнений с вырожденным ядром, но верно для любых ядер.
Пусть
уравнение (1), (8) имеет единственное
решение ,
а соответствующее ему однородное
уравнение имеет ненулевое решение
,
а соответствующее ему однородное
уравнение имеет ненулевое решение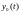 .
Тогда неоднородное уравнение имеет еще
одно решение
.
Тогда неоднородное уравнение имеет еще
одно решение
Пусть
однородное уравнение имеет только
нулевое решение, а неоднородное – два
различных и
и .
Тогда их разность
.
Тогда их разность является
решением однородного уравнения, поэтому
оно нулевое, т.е.
является
решением однородного уравнения, поэтому
оно нулевое, т.е.
Теорема 2. (существования решения уравнения (1) Фредгольма)
Для уравнения
(1) с непрерывным ядром на квадрате
на квадрате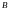 ,
свободным членом
,
свободным членом
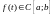 существует
число
существует
число такое,
что для всех
такое,
что для всех уравнение
(1) имеет решение
уравнение
(1) имеет решение
Док.
Обозначения:
Для нахождения
решения применим метод последовательных
приближений. Определим функциональную
последовательность из
непрерывных на
функций:
из
непрерывных на
функций:
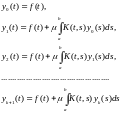
Рассмотрим функциональный ряд
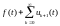 (9)
(9)
где .
Заметим, что
.
Заметим, что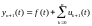 .
.
Оценим модули членов ряда (9):
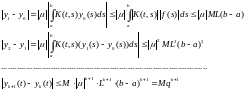
Здесь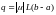 .Если
.Если ,
то
,
то
 оцениваются
сверху членами сходящейся геометрической
прогрессии, что по признаку Вейерштрасса
обеспечивает равномерную сходимость
ряда (9) и непрерывность его суммы
оцениваются
сверху членами сходящейся геометрической
прогрессии, что по признаку Вейерштрасса
обеспечивает равномерную сходимость
ряда (9) и непрерывность его суммы .
.
Покажем, что – решение уравнения (1)
Частичная
сумма ряда (9) ,
поэтому возможен предельный переход:
,
поэтому возможен предельный переход:
Теорема 3 (существования решения для уравнений Вольтерра)
Для уравнения
(8) с непрерывным ядром
на
треугольнике ,
любым свободным членом
существует
и единственное его решение
при всех
,
любым свободным членом
существует
и единственное его решение
при всех .
.
Док. Подобно тому, что было в теореме 2.
Функциональная последовательность непрерывных на определяется рекуррентными соотношениями:

Оценка модулей членов ряда (9) меняется:

Мажорирующий ряд сходится при любом значении , поэтому сумма равномерно сходящегося ряда (9) существует и является решением уравнения (8). В доказательстве единственности решения уравнения (8) используется неравенство Гронуолла – Беллмана:
Для любых
непрерывных функций и
числа
и
числа связанных
неравенством
связанных
неравенством

справедливо неравенство

Пусть
уравнение (8) имеет два решения
и .
Тогда
.
Тогда

Обозначая
через и
полагая
и
полагая ,
получим, что для неотрицательной функции
,
получим, что для неотрицательной функции справедливо неравенство
справедливо неравенство .
Тогда по неравенству Г-Б, имеем
.
Тогда по неравенству Г-Б, имеем
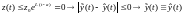
Следствие. Однородное уравнение, соответствующее уравнению (8) всегда имеет только нулевое решение, а значит оператор Вольтерра не имеет ни одного характеристического числа (пустой спектр)
