Лекции, Гришин С.А. / Voprosy_po_DIU

Экзаменационные вопросы по курсу ДИА, весна-23

1. Устойчивость решения ДУ по Ляпунову, асимптотическая устойчивость. Теорема об устойчивости нулевого решения системы ДУ с постоянными коэффициентами. Критерий Раусса- Гурвица (без док.).

2. Понятие функции Ляпунова. Теорема об устойчивости Ляпунова.

3. Теорема об асимптотической устойчивости.

4. Устойчивость по первому приближению. Теорема об устойчивости по первому приближению.

5. Понятие первого интеграла системы ДУ. Независимость первых интегралов. Теорема о существовании первых интегралов.

6. Однородное линейное уравнение первого порядка с частными производными. Теорема о связи его решений с первыми интегралами системы ДУ для характеристик.

7. Теорема о структуре общего решения линейного уравнения первого порядка с частными производными. Постановка задачи Коши.

8. Квазилинейные неоднородные уравнения первого порядка с частными производными. Теорема о связи его решений с первыми интегралами системы ДУ для характеристик. Постановка задачи Коши.

9. Тригонометрические ряды Фурье. Бесконечная система ортогональных тригонометрических функций с периодом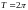 . Теорема о поточечной сходимости ряда Фурье (без док).

10. Тригонометрические ряды Фурье функций с периодом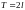 . Разложение функций, заданных на отрезке , четные и нечетные продолжения. Комплексная форма ряда Фурье.

11. Обобщенные ряды Фурье по ортогональной системе элементов бесконечномерных евклидовых пространств. Экстремальное свойство коэффициентов ряда Фурье. Неравенство Бесселя и равенство Парсеваля.

12. Замкнутые и полные системы ортогональных элементов бесконечномерных евклидовых пространств. Необходимое и достаточное условие замкнутости системы. Теорема о полноте замкнутой системы ортогональных элементов.

13. Интеграл Фурье для непериодических функций на всей числовой оси. Различные формы записи интеграла Фурье. Теорема о поточечной сходимости интеграла Фурье (без док.). Интегралы Фурье для функций, заданных на положительной полуоси: четные и нечетные продолжения. Комплексная форма интеграла Фурье.

14. Преобразование Фурье и его основные свойства. Косинус-преобразования и синус-преобразования.

15. Операторы: линейные, ограниченные, непрерывные. Норма оператора. Примеры. Сопряженные операторы: линейность, единственность. Собственные элементы и характеристические числа оператора.

16. Теорема существования сопряженного оператора для интегрального оператора с непрерывным ядром.

17. Самосопряженные операторы: действительность характеристических чисел, ортогональность собственных элементов с различными характеристическими числами. Конечность или счетность спектра самосопряженного оператора.

18. Интегральные уравнения Фредгольма второго рода: теорема существования решения при малых значениях параметра, метод последовательных приближений.

19. Интегральные уравнения Вольтерра второго рода: теорема существования решения при любых значениях параметра, метод последовательных приближений.

20. Степени оператора Фредгольма, итерированные ядра, резольвента оператора.

21. Степени оператора Вольтерра, итерирующие ядра, резольвента

22. Интегральные уравнения Фредгольма с симметричным ядром. Формулы Шмидта 1 для его решения в случае, когда параметр не принадлежит спектру оператора.

23. Интегральные уравнения Фредгольма с симметричным ядром. Формулы Шмидта 2 и условия разрешимости уравнения в случае, когда параметр принадлежит спектру оператора.

24. Краевая задача для дифференциального уравнения второго порядка. Задача Штурма-Лиувилля. Свойства собственных чисел и собственных функций задачи Ш-Л.

25. Функция Грина регулярной, однородной краевой задачи. Теорема о существовании и единственности функции Грина.

26. Теорема Гильберта о существовании и единственности решения неоднородной краевой задачи.

27. Теорема об эквивалентности решения задачи Ш-Л для дифференциального оператора второго порядка и задачи на собственные значения интегрального оператора с симметричным ядром.