Лекции, Гришин С.А. / DIU-lektsia_9_Integraly_Furye

ДИУ-лекция 9 по теме «Интеграл Фурье»

П.1 Формула Фурье

Пусть функция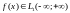 , т.е. для нее существует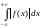 , не является периодической. Рассмотрим 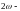периодическую функцию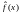 , для которой .

Предположим, что функция раскладывается в ряд Фурье:

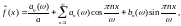(1)

где .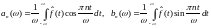

Подставляя коэффициенты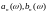 в (1) и преобразуя полученное выражение, получим

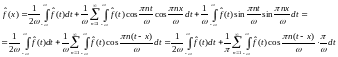
Обозначение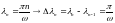 . Тогда

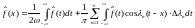
Заметим, что величина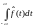 ограничена по :

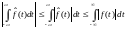
и ее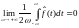 . Второе выражение является интегральной суммой для несобственного интеграла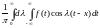 . Если он сходится, то справедлива интегральная формула Фурье

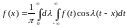, (2)

а ее правая часть называется интегралом Фурье.

Внутренний несобственный интеграл в (2) понимается в смысле главного значения.

Если функция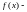 четная, то формула (2) примет вид:

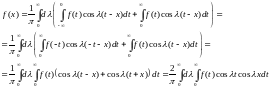
Тогда интегральная формула Фурье для четных функций имеет вид:

(3)

Аналогично, для нечетных функций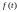 имеет место представление:

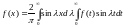(4)

Преобразуем интеграл Фурье (2) в иную форму:

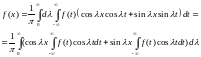
Тогда

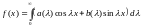, (5)

где

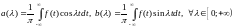(6)

Правую часть равенства (5) также называют интегралом Фурье. Для четных функций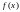 формулы (6) принимают вид

(7)

Для нечетных :

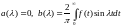(8)

Отметим некоторые свойства функций :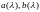

1. Если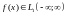 , то - непрерывные функции на полуоси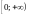

Докажем непрерывность . Интеграл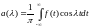 сходится для любой функции , причем сходимость по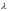 равномерная. Пусть любая точка полуоси .

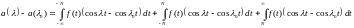
Тогда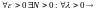

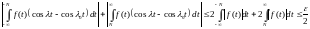
Оценим второй интеграл с учетом неравенства :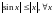

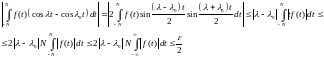
Объединяя две оценки, получим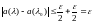

Доказательство непрерывности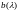 аналогичное.

2.

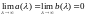
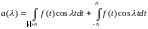
Первый интеграл оценивается: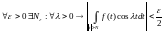

Второй интеграл оценивается с помощью леммы Римана: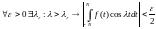

Объединяя обе оценки, получим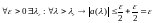

Пример. Представить функцию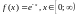 в виде интеграла Фурье по косинусам и синусам.

Воспользуемся формулой (7) и (8):

,

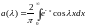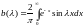
Проинтегрируем оба интеграла по частям:

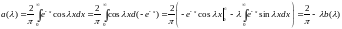
Аналогично,

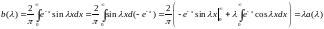
Находим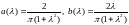 и разложения

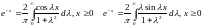
Пример. Представить функцию интегралом Фурье, продолжив ее как четную функцию на отрицательную полуось.

Воспользуемся формулой (7):

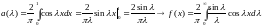
Полагая в этой формуле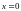 , получим .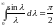

П. Поточечная сходимость интеграла Фурье.

Теорема (о по точечной сходимости)

Пусть удовлетворяет условиям:

1. кусочно- гладкая на каждом конечном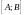 числовой оси;

2. в каждой точке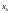 разрыва функции существуют ;

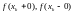3. в каждой точке разрыва производной существуют односторонние производные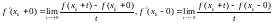

4.

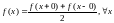
Тогда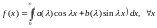 , где

П. Комплексная форма интеграла Фурье

Пусть функция удовлетворяет условиям теоремы о поточечной сходимости. Тогда для любой точки справедлива формула Фурье:

В силу четности функции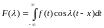 имеем .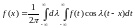

В силу нечетности функции .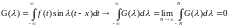

Тогда

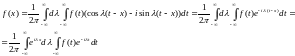
Если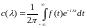 , интеграл Фурье примет форму

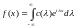(9)

которая называется комплексной формой интеграла Фурье

Пример. Представить интегралом Фурье функцию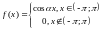

Решение

Тогда