Отчет по практическому заданию №2

МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра микро- и наноэлектроники

отчет по практическому заданию по дисциплине «Физика полупроводников» Тема: Моделирование эллипсоидов эффективной массы в среде Mathcad

Студенты гр. 1283 ____________________ ____________________ Григорьева В.В. Ганиев Ж. Преподаватель __________________________ Зубков В.И.

Санкт-Петербург 2024

Построили эллипсоиды эффективной массы для различных полупроводников. Все эллипсоиды будут задаваться через сферические координаты, само построение будет проводиться в декартовых координатах.

Рисунок 1 – Фрагмент кода, создающий массив точек построения

Значения m₁, m₂ и m₃ – продольные и поперечное значения эффективной массы соответственно в безразмерных единицах. Как правило, продольные составляющие равны, а поперечная составляющая превышает продольную примерно в два раза. В результате мы получаем поверхность, называемую эллипсоидом вращения.

Арсенид галлия (GaAs) – прямозонный полупроводник, минимум зоны проводимости которого находится в точке Г₁ или Г₆, если проводится учет спина и спин-орбитального взаимодействия.

Рисунок 2 – Сфера эффективной массы зоны проводимости для GaAs

Рисунок 3 – Двумерная модель эллипсоидов эффективной массы в арсениде галия

Кремний (Si). Имеем шесть эллипсоидов вращения, ориентированных вдоль осей декартовой системы координат – в направлениях (100), (010), (001) и обратных данным. Минимум зоны проводимости в кремнии находится в точке Δ₁.

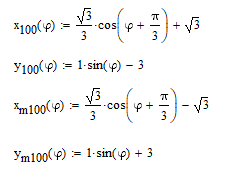
Рисунок 4 – Фрагмент кода, создающий массив точек построения для 2д кремния

Рисунок 5 – Двумерная модель эллипсоидов эффективной массы в кремнии

Рисунок 6 – Эллипсоиды эффективной массы зоны проводимости для Si

Германий (Ge). Данный полупроводник имеет минимум зоны проводимости в точке L₁⁺ . В данном случае мы будем иметь 8 половин эллипсоидов или 4 полных эллипсоида, ориентированных в направлениях (111), (11-1) и др. В данном случае способ построения отличается заданием эллипсоида через внутреннюю функцию Mathcad 15 – CreateMesh, которая так же содержит в себе матрицу поворота fmap1, которая и производит вращение поверхности относительно начала координат.

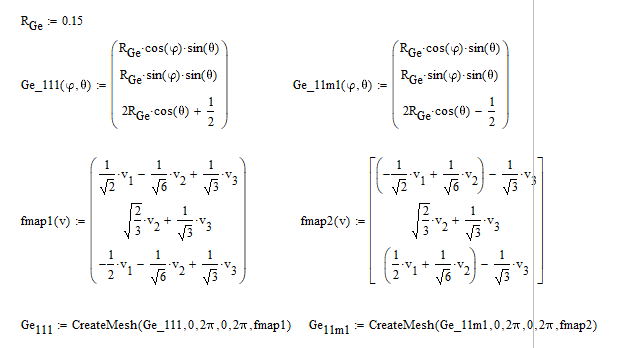
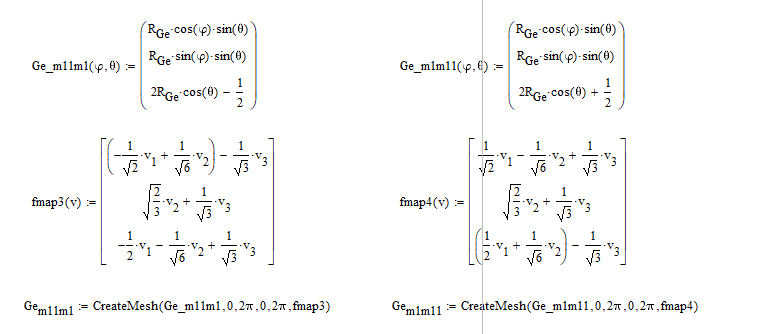
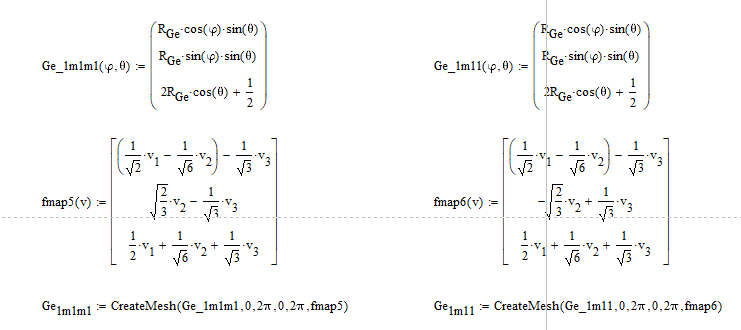
Рисунок 10 – Фрагмент кода, создающий массив точек и поворачивающий созданный из полученных данных эллипсоид в направлении (1 1 1)

Рисунок 11 – Эллипсоиды эффективной массы зоны проводимости для Ge

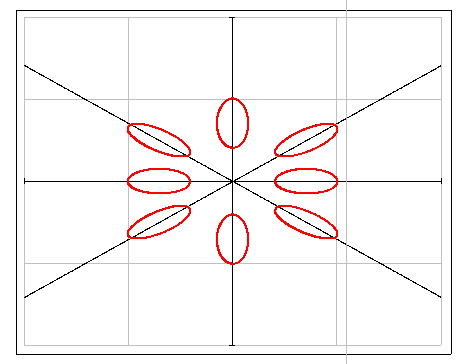
Рисунок 12 – Двумерная модель эллипсоидов эффективной массы в германии

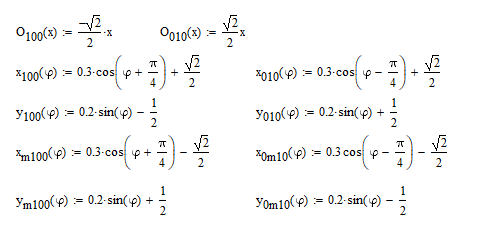
Рисунок 13 – Фрагмент кода, создающий массив точек построения для 2д германия