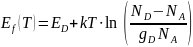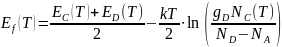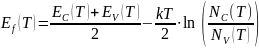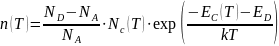идз1283ФПП
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра микро- и наноэлектроники
отчет
по лабораторной работе
по дисциплине «Физика полупроводников»
Тема: «Статистика электронов в полупроводниках»
Вариант №5
Студенты гр. 1283 |
|
Григорьева В.В. |
|
|
Ганиев Ж. |
Преподаватель |
|
Кучерова О.В. |
Санкт-Петербург
2024
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1.Свойства
Монокристаллический арсенид индия (InAs) – полупроводник с малой шириной запрещённой зоны представляет интерес для полупроводниковой опто- и микрофотоэлектроники, как материал с малой шириной запрещённой зоны, имеющий высокую квантовую эффективность при поглощении излучения в диапазоне длин волн 0,5 – 3,46 мкм (при температуре 300 К). Бинарное неорганическое соединение индия и мышьяка. Химическая формула соединения InAs.
Зонная диаграмма арсенида индия представлена на рисунке 1.
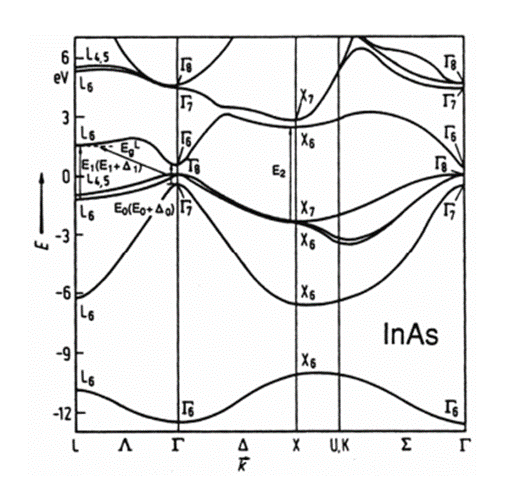
Рисунок 1 – Зонная диаграмма арсенида индия при Т = 300 К
Является прямозонным полупроводником, относящимся к полупроводникам группы AIIIBV. Имеет ширину запрещённой зоны около 0.354эВ.
Ввиду низкой ширины запрещённой зоны большинство полупроводниковых приборов, изготовленных из этого материала, работают только при криогенных или очень низких температурах.
В таблице 1 представлены основные параметры исследуемого материала.
Таблица 1 – Основные параметры InAs
Постоянная решётки |
а = 0,605 нм |
Eg при Т = 300 К |
0,17 эВ |
Eg при Т = 77 К |
0,23 эВ |
Eg при Т = 0 К |
0,354 эВ |
Эффективная масса электронов проводимости |
m*e = 0,023m0 |
Эффективная масса дырок |
m*p = 0,41m0 |
Подвижность электронов при Т = 77 К |
1,1⋅106 см²/(В·с) |
Подвижность дырок при Т = 77 К |
9,1⋅103 см²/(В·с) |
Собственная концентрация носителей заряда |
2,0·1016 см-3 |
Удельное сопротивление |
4·10-3 Ом·см |
Нелегированный арсенид индия обладает очень высокой подвижностью электронов (около 78 000 см²/(В·с) при Т = 300 К), а также имеет большую длину свободного пробега электронов (до 0,7 мкм при 300 K).
2. Получение
Пластины InAs можно получить методом Чохральского по технологии LEC.
3.Применение
Применяется для изготовления сверхвысокочастотных транзисторов, а также светодиодов и фотодиодов, работающих в инфракрасной области электромагнитного излучения, датчиков Холла магнитного поля, для организации ансамблей квантовых точек в некоторых полупроводниковых приборах.
4. Выбор примеси
Атомы примесей IV группы могут занимать как узлы А3, так и В5, проявляя донорные или акцепторные свойства. Замещение должно со-провождаться наименьшей деформацией кристаллической решётки. Поэтому критерием донорного или акцепторного действия таких примесей может служить соответствие размеров замещающего и замещаемого атомов. В InAs они замещают In и являют донорами, возьмём Si. Наиболее часто на практике для создания р-п переходов используются Zn (акцептор), который обладает высокой растворимостью в полупроводниках A3B5
Si Ed = 0.395
Zn Ea = 0.01
РАСЧЕТНАЯ ЧАСТЬ
Определение эффективных плотностей состояния в валентной зоне и зоне проводимости:
Расчет температурных зависимостей эффективных плотностей состояний в зоне проводимости и в валентной зоне проведём, используя соотношения (1) и (2):
-
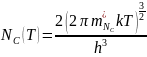
(1)
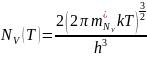
(2)
Пример расчёта для Т = 300 К:
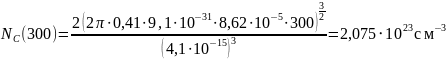
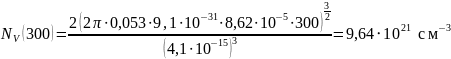
Найдем также эффективные массы плотностей состояния:
Для зоны проводимости:
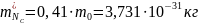
Для валентной зоны:
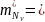
Определение зависимости ширины запрещённой зоны от температуры:
Температурная зависимость ширины запрещенной зоны рассчитывается по формуле:
-
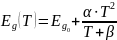 ,
,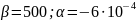
(3)
где, Eg0 – ширина запрещённой зоны при 0 К
Середина
запрещенной зоны при 0 К будет равна
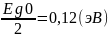
Используя это значение, можно найти положение валентной зоны и зоны проводимости по формулам:
-
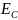 (T)
=
(T)
=
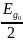 +
+
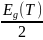
(4)
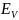 (T)
=
(T)
=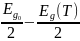
(5)
Пример
расчёта для
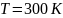 :
:
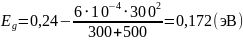
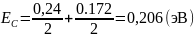
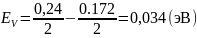
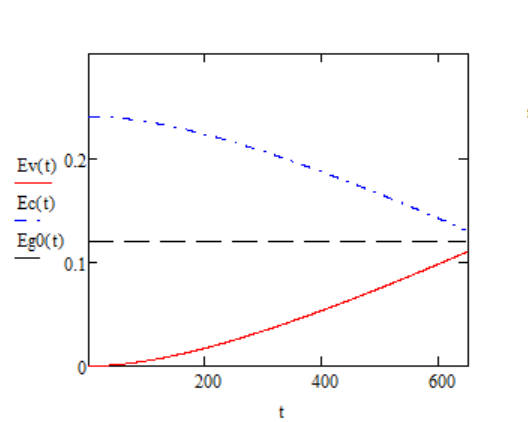
Рис. 2 – Зависимость ширины запрещенной зоны от температуры
Определение положения уровня Ферми:
Для определения положения уровня Ферми надо решить уравнение электронейтральности. Его общий вид:
-
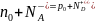
(6)
В этой формуле:
-
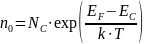
(7)
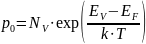
(8)
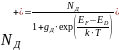
(9)
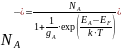
(10)
где gA и gD факторы вырождения примесей, равные соответственно 0,3495 для цинка и 0,29 для селена.
При низких температурах энергия ионизации доноров намного меньше энергии ионизации акцепторов и поэтому преобладает электронная проводимость. Уравнение электронейтральности примет вид:
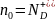
Решив уравнение, получаем значения уровня Ферми при низких температурах:
|
(11) |
При повышении температуры атомы акцепторной примеси оказываются полностью ионизированы и электроны с донорной примеси полностью заполняют акцепторный уровень. Тогда уравнение электронейтральности и его решение, с учетом сильной компенсации, примут вид:
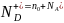
|
(12) |
При высоких температурах наблюдается участок собственной проводимости, так как все примеси оказываются ионизированы. Уравнение электронейтральности и его решение:
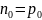
|
(13) |
Постоим зависимость уровня Ферми от температуры в различных температурных диапазонах на одном графике:
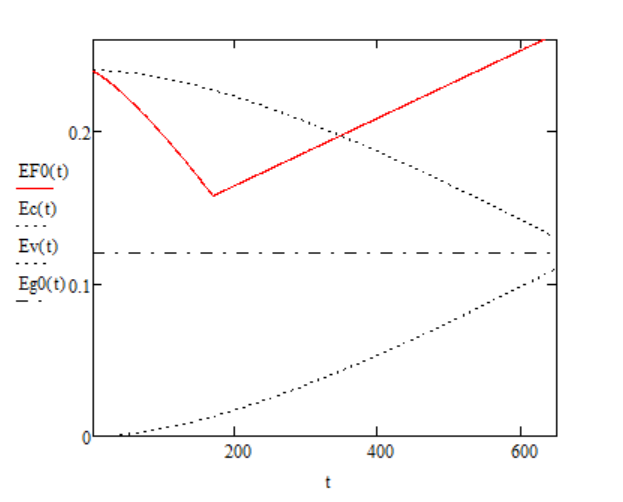
Рис. 3 – Зависимость положения уровня Ферми от температуры
4. Расчет температурной зависимости концентраций основных носителей заряда:
В полупроводнике преобладает донорная примесь ( ND > NA). Можно сказать, что компенсирующая примесь полностью ионизирована, так как на акцепторной примеси имеются свободные состояния для электронов.
При низких температурах и n0
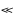 ND и n0 < ND–NA,
уравнение электронейтральности будет
иметь вид:
ND и n0 < ND–NA,
уравнение электронейтральности будет
иметь вид:
|
(14) |
При повышении температуры и при NA n0 ND, получим:
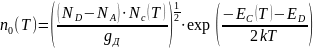
На
участке полной ионизации при концентрациях
p0
ND - NA и n0
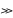 p0, будем искать концентрацию
так:
p0, будем искать концентрацию
так:
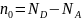
При дальнейшем повышении температуры будет наблюдаться участок собственной проводимости, где концентрацию можно найти:
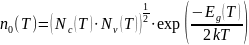


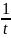
 остроим
температурную зависимость концентрации
основных носителей заряда:
остроим
температурную зависимость концентрации
основных носителей заряда:
Рис. 4 – Зависимость концентрации электронов от температуры
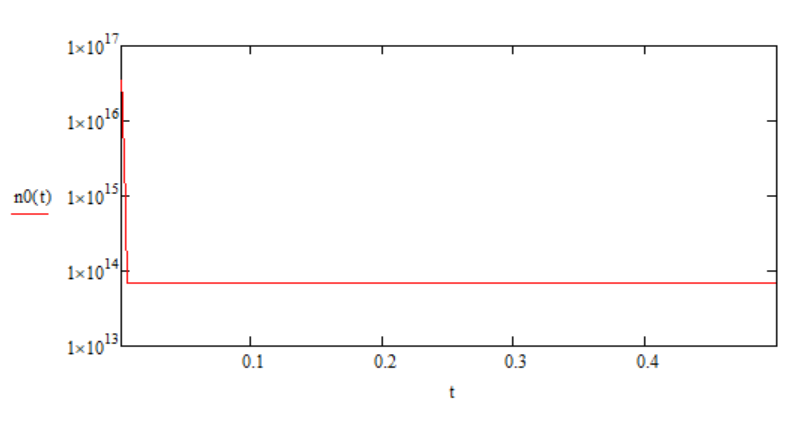
На заданном температурном диапазоне не наблюдается участок неполной ионизации примеси. Это связано с очень малой энергией ионизации селена. На следующем графике покажем, что данный участок наблюдается при Т ≈ 0 К.
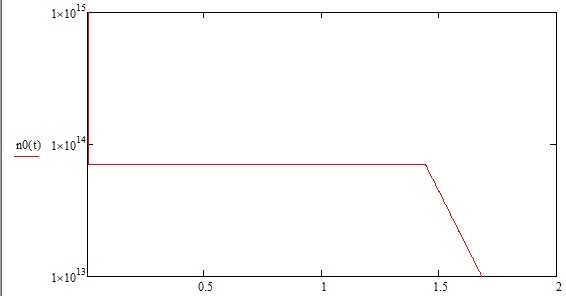
Рис. 5 – Зависимость концентрации электронов от температуры на расширенном диапазоне температур
Вывод
В ходе данной лабораторной работы были проведены расчёты энергии Ферми и концентрации основных носителей заряда в арсениде индия InAs, компенсированным селеном Se и цинком Zn. Были представлены основные методы получения данного полупроводника и его области применения.
Арсенид индия является одним из самых узкозонных полупроводников. Учитывая данный факт, легировать его возможно лишь примесями с малой энергией ионизации. Таким образом были выбраны селен и цинк. Из-за их малой энергии ионизации, участок неполного истощения примеси наблюдается при очень малых температурах, близких к 0 ÷ 1 К, что и отражено на рис. 5. При этом участок собственной проводимости также начинается довольно рано – в области температур Т ≈ 170 К.
Ранее было показано (рис. 3), что уровень Ферми переходит в область зоны проводимости примерно при Т ≈ 350 К. Полупроводник в этой области становится сильно вырожденным и ведет себя подобно металлу. Поэтому использовать данный полупроводник рекомендуется лишь при низких температурах, на практике – при температуре кипения азота (Т = 77 К).