AGG BLP 1

Федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

им. В.И. Ульянова (Ленина)»

кафедра микро- и наноэлектроники

ОТЧЁТ

по ИДЗ

по дисциплине «Физика полупроводников» №1

«Моделирование плоской волны и волнового пакета»

Выполнили: Григорьева В.В., Ганиев Ж.

Группа № 1283

Преподаватель: Зубков В. И.

Санкт-Петербург,

2024

Моделирование плоской волны и волнового пакета

Задача: провести в программной среде Mathcad моделирование плоской волны и волнового пакета.

Теоретические положения:

Плоская волна: плоская монохроматическая волна является решением уравнения колебания струны. В одномерном случае уравнение имеет вид:

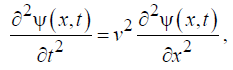
где множитель v² имеет размерность квадрата скорости.

Решение уравнения

где k = 2π/λ – волновое число (волновой вектор в трехмерном случае); λ – длина волны; ω = 2π/T– круговая частота; T – период волны. Отсюда фазовая скорость v = v_ф = ω/k – это скорость движения точек монохроматической волны с одинаковой фазой.

Волновой пакет: Принятое в физике твердого тела сопоставление электрону монохроматической волны де Бройля является довольно грубым приближением, так как такая инфинитная (не имеющая начала и конца) волна обладает бесконечно большой энергией E. Более корректно частице сопоставлять волну конечной протяженности, т. е., строго говоря, следует использовать волновой пакет, локализованный в области с размерами 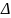x 1/ k.

Волновой пакет строится из суперпозиции плоских волн, для которых волновое число k изменяется от k₀ – k/2 до k₀ + k/2 (для простоты предполагается, что на имеющем основное значение интервале амплитуды остаются постоянными и равными A/ k:

Групповая скорость v_гр = dω/dk характеризует среднюю скорость распространения такой группы волн (вейвлета); групповая скорость также определяет скорость переноса энергии вейвлетом.

Практическая часть:

1. Проведём моделирование статической однородной плоской волны. Для этого зададим волну с помощью функции sin(kx–ωt) и построим график соответствующий график:

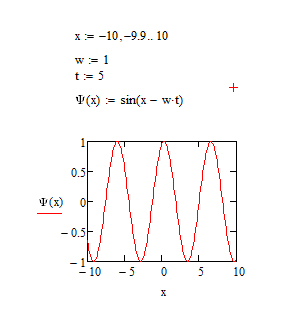
Рис. 1. Моделирование статистической одномерной плоской волны

2. Теперь выполним моделирование двумерной плоской волны. Для этого нужно задать функцию Y от двух переменных – x и y. График построим с помощью функции «график поверхности»:

Рис. 2. Моделирование статистической двумерной плоской волны

3. Следующим этапом запрограммируем анимационное движение волны с помощью переменной FRAME. Анимацию возможно посмотреть в файле «VAWES.xmcd», прилагаемому к данному отчёту. Для удобства динамические и статические волны будем рассматривать отдельно,для этого для динамических волн будем использовать функцию U. Сама функция будет выглядеть следующим образом для одномерной и двумерной динамической волны соответственно:

   Рис. 3. Функции динамической одномерной и двумерной плоской волны
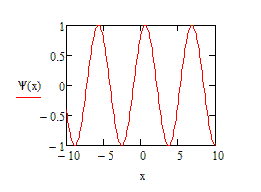
   Рис.4. Скриншоты анимирования одномерной плоской волны
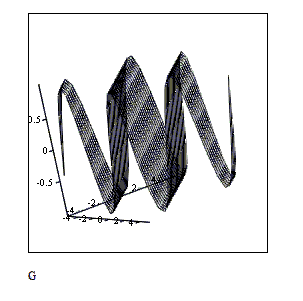
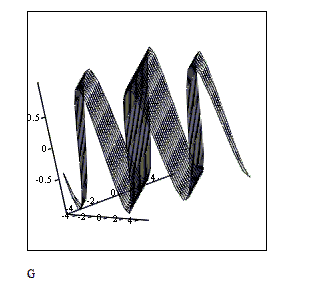
   Рис.4. Скриншоты анимирования двумерной плоской волны

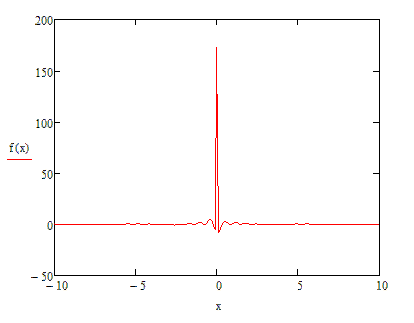
4. Теперь рассмотрим пакет волн. Для него точно так же начнем с моделирования статического одномерного случая через интеграл:

Рис. 5. Моделирование статистической одномерной пакет

5. Моделирование двумерного пакета задаётся аналогично одномерному – через переменные x и y. График построим с помощью функции «график поверхности»:

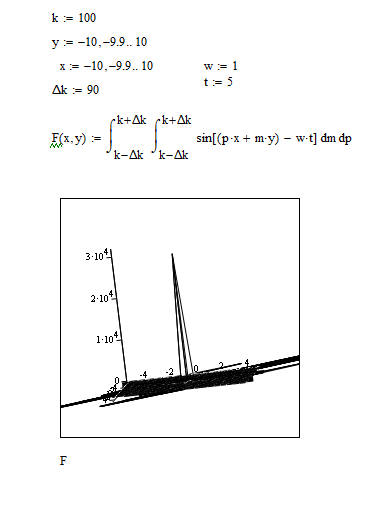
Рис. 6. Моделирование статистической двумерной плоской волны

Последним этапом запрограммируем анимационное движение пакета волн с помощью переменной FRAME. Анимации пакета волн также возможно посмотреть в файле «VAWES.xmcd», прилагаемому к данному отчёту. А функция примет новый вид:

Рис. 7. Функции динамического одномерного и двумерного пакетов
Рис.8. Скриншоты анимирования одномерного пакета
Рис.9. Скриншоты анимирования двумерного пакета