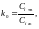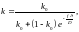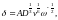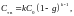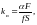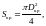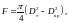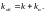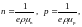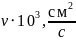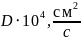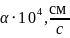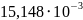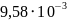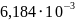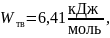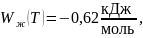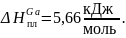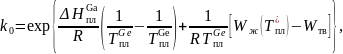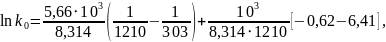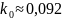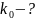Практическое задание №1

МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра микро- и наноэлектроники

отчЁт по практическому заданию № 1 по дисциплине «Технология материалов и эпитаксиальных структур» Тема: Легирование кристаллов при выращивании методом Чохральского Вариант №5

Студентка гр. 1283 ____________________ Григорьева В.В. Преподаватель __________________________ Бобков А.А.

Санкт-Петербург 2024

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

На рисунке 1 приведём схему установки для выращивания кристаллов методом Чохральского.

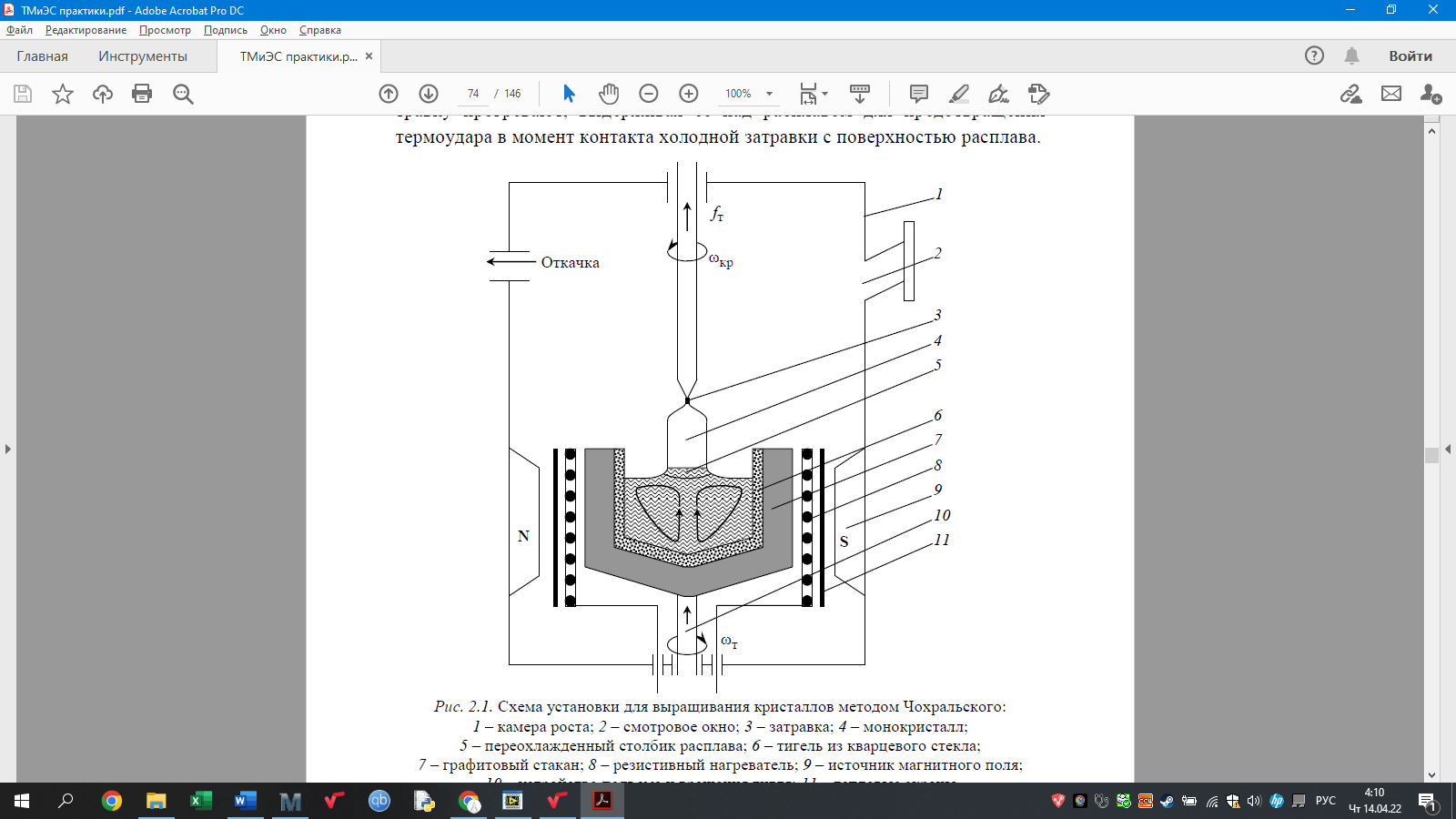
Рисунок 1 – Схема установки для выращивания кристаллов методом Чохральского

Элементы установки:

1.	Камера роста	2.	Смотровое окно
3.	Затравка	4.	Монокристалл
5.	Переохлаждённый столбик расплава	6.	Тигель из кварцевого стекла
7.	Графитовый стакан	8.	Резистивный нагреватель
9.	Источник магнитного поля	10.	Устройство подъёма и вращения тигля
11.	Тепловые экраны

Соотношения, используемые в расчётах.

Соотношение (1) – равновесный коэффициент распределения примеси – характеризует отношение концентрации примеси в твёрдой и жидкой фазах в условиях термодинамического равновесия.

(1)

где C_{i тв} – концентрация примеси в твёрдой фазе,

C_{i ж} – концентрация примеси в жидкой фазе.

Если скорость кристаллизации имеет конечное значение, то перед фронтом кристаллизации по мере роста кристалла образуется слой расплава с эффективной толщиной δ, обогащённый или обеднённый примесью, если k₀ меньше или больше единицы соответственно.

В этих условиях содержание примеси в закристаллизовавшейся части

слитка С_тв будет определяться концентрацией примеси в расплаве у фронта кристаллизации С_тв = k₀С_ж0. Значение С_ж0, как правило, неизвестно, поэтому в неравновесных условиях связь между концентрациями примеси в твёрдой С_тв и жидкой С_ж фазах осуществляют с помощью эффективного коэффициента распределения k, который задаётся выражением (2) – уравнение Бартона-Прима-Слихтера, связывающее равновесный и эффективный коэффициенты распределения.

(2)

где f – скорость кристаллизации (0,5…5 мм/мин),

D – коэффициент диффузии примеси в жидкой фазе, см²/с,

δ – толщина диффузионного слоя, определяемая соотношением (3) (0,1…10^-3 см).

(3)

где А – численный коэффициент, принимающий значения 1…2 (для МЧ – 1,6),

v – кинематическая вязкость жидкости, см²/с,

ω – скорость вращения кристалла относительно тигля, рад/с.

Закон распределения примеси вдоль слитка – соотношение (4) – уравнение Галливера:

(4)

где g – доля закристаллизовавшегося расплава, равная отношению текущего и начального объёмов.

Приведённый коэффициент испарения имеет смысл в случае легирования кристалла летучей примесью, он определяется соотношением (5).

(5)

где S – площадь поперечного сечения кристалла – соотношение (6),

α – линейный коэффициент испарения (коэффициент межфазного взаимодействия),

F – площадь поверхности испарения, рассчитываемая с использованием соотношения (7).

(6)

где D_кр – диаметр кристалла.

(7)

где D_т – диаметр тигля.

Тогда имеет смысл ввести обобщённый коэффициент распределения, учитывающий как эффективный коэффициент распределения, так и коэффициент испарения – соотношение (8).

(8)

Концентрация носителей заряда может быть рассчитана с использованием соотношений (9).

(9)

где е = 1,6 · 10^-19 Кл,

ρ – удельное сопротивление, которое может быть определено из марки выращиваемого полупроводника,

μ_n и μ_p – подвижности электронов и дырок в полупроводнике при определённой температуре.

РАСЧЁТНАЯ ЧАСТЬ

Параметры, используемые в расчётах – таблица 1

Таблица 1 – Используемые значения параметров для Ge, легированного Ga, и для Ge, легированного Sn

Материал
	1,35	8,7	0,7	-
		2	1,26	1,2

1. Построить зависимость С_тв(g) для различных скоростей кристаллизации Ge, легированного Ga. Скорость вращения кристалла относительно тигля 60 об/мин. Скорость кристаллизации 0,5; 5; 10 мм/мин. Начальная концентрация примеси в расплаве 10¹⁵ см^-3. Построить график зависимости k_эфф как функции скорости кристаллизации при скорости вращения кристалла относительно тигля 60 об/мин. Для указанных скоростей кристаллизации записать в таблицу значения k_эфф.

Таблица 2 – Расчётные значения k_эфф для различных скоростей кристаллизации

Скорость кристаллизации f, мм/мин	0,5	5	10
kэфф · 103	95,63	212,54	433,26

1. Переведём заданные величины – скорости кристаллизации f_i и скорость вращения кристалла относительно тигля ω – в удобные для расчёта единицы измерения:

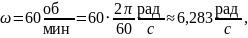
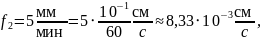
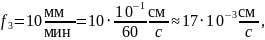
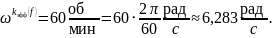
2. Рассчитаем значение толщины диффузионного слоя δ для первого случая – ω = 60 об/мин. Учтём, что для метода Чохральского – А = 1,6:

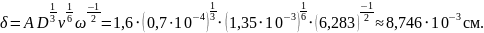
3. Проведём расчет значений эффективного коэффициента распределения k_эфф для различных значений скорости кристаллизации:

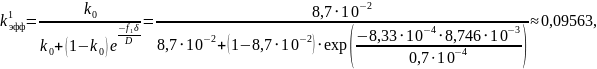
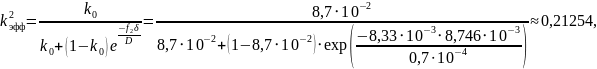
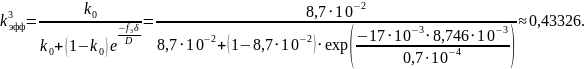
4. Полученным значениям эффективного коэффициента распределения сопоставим зависимости концентрации твёрдой фазы С_тв(g) = kC₀(1–g)^k–1. Полученные зависимости аналитически представим на рисунке 1:

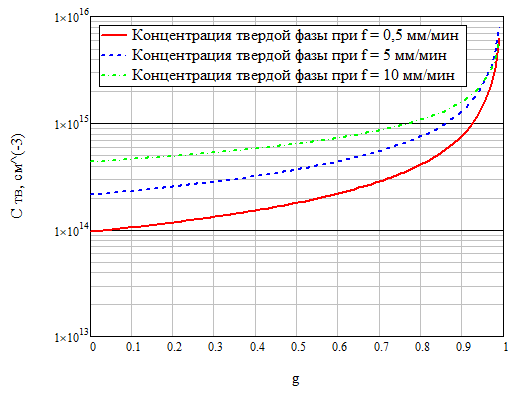
Рисунок 1 – График зависимостей концентрации твёрдой фазы от соотношения объёма твёрдой фазы и полного объёма при различных скоростях кристаллизации

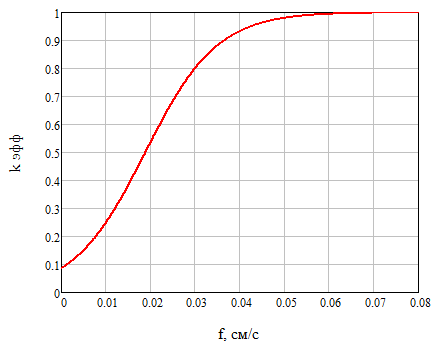
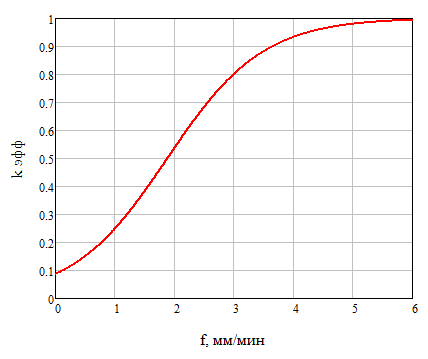
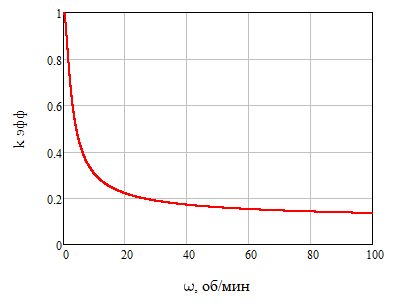
5. Построим график зависимости эффективного коэффициента распределения k_эфф от скорости кристаллизации f при скорости вращения кристалла относительно тигля ω = 60 об/мин на рисунке 2:

а)	б)

Рисунок 2 – Графики зависимостей эффективного коэффициента распределения от скорости кристаллизации при скорости вращения кристалла относительно тигля 60 об/мин

(а – скорость кристаллизации в см/с, б – скорость кристаллизации в мм/мин)

2. Построить зависимость С_тв(g) для различных скоростей кристаллизации Ge, легированного Ga. Скорость кристаллизации 3 мм/мин. Скорость вращения кристалла относительно тигля составляет 20; 50; 120 об/мин. Начальная концентрация примеси в расплаве 10¹⁵ см^-3. Построить графики зависимости толщины диффузионного слоя δ и k_эфф как функции скорости вращения кристалла относительно тигля при скорости кристаллизации 3 мм/мин. Для указанных скоростей кристаллизации записать в таблицу значения δ и k_эфф.

Таблица 3 – Расчётные значения k_эфф и δ для различных относительных скоростей вращения кристалла относительно тигля

ω, об/мин	20	50	120
kэфф · 103	219,454	158,889	129,081
δ, см

1. Переведём заданные величины – скорости кристаллизации f_i и скорость вращения кристалла относительно тигля ω – в удобные для расчёта единицы измерения:

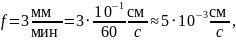
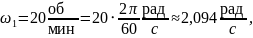
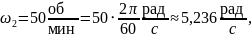
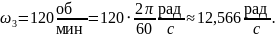
2. Рассчитаем значение толщин диффузионного слоя δ для всех случая. Учтём, что для метода Чохральского – А = 1,6:

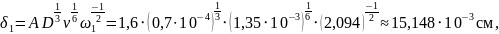
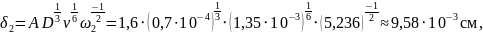
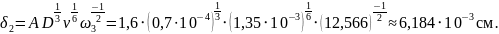
3. Проведём расчет значений эффективного коэффициента распределения k_эфф для различных значений скорости кристаллизации:

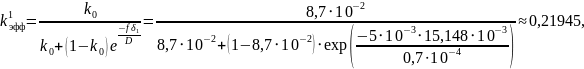
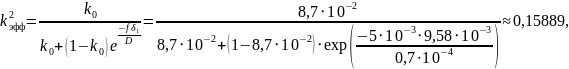
4. Полученным значениям эффективного коэффициента распределения сопоставим зависимости концентрации твёрдой фазы С_тв(g) = kC₀(1–g)^k–1. Полученные зависимости аналитически представим на рисунке 1:

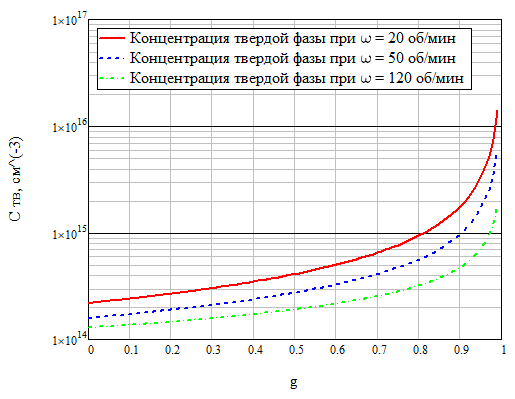
Рисунок 3 – График зависимостей концентрации твёрдой фазы от соотношения объёма твёрдой фазы и полного объёма при различных скоростях кристаллизации

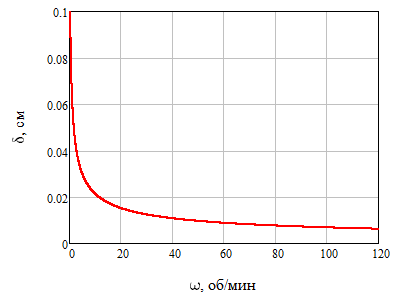
5. Построим график зависимости эффективного коэффициента распределения k_эфф и диффузионного слоя δ от скорости вращения кристалла относительно тигля ω при скорости кристаллизации f = 3 мм/мин при на рисунке 2:

а)	б)

Рисунок 4 – Графики зависимостей эффективного коэффициента распределения от скорости вращения кристалла относительно тигля при скорости кристаллизации 3 мм/мин

(а – толщина диффузионного слоя, б – эффективный коэффициент распределения)

3. Рассчитаем значения равновесного коэффициента распределения Ga в рамках модели регулярных растворов, применяя для твёрдой фазы приближение регулярных растворов, а для жидкой – квазирегулярных. Также рассчитаем значения абсолютной и относительной погрешностей вычислений.

Дано:	Решение:
	Ответ:0,092;

4. (5.) Построить зависимости С_тв(g) для кристалла ГЭМ-7,2 при следующих параметрах технологического процесса: скорость кристаллизации 0,3 мм/мин, скорость вращения кристалла относительно тигля 60 об/мин, диаметр кристалла – 4 см, диаметр тигля – 12, 20, 25 см. Начальную концентрацию примеси в расплаве определить по указанному значению удельного сопротивления и условий технологического процесса. Для указанных параметров технологического процесса записать в таблицу значения параметров k_эфф и k_об.

Таблица 4 – Расчётные значения F, k_эфф, k_и и k_об для различных значений диаметра тигля

Dт, см	F, см2	k	kи	kоб
12	100,53	0,024	1,92	1,944
20	301,59		5,76	5,784
25	478,31		9,135	9,159

1. Переведём заданные величины – скорости кристаллизации f_i и скорость вращения кристалла относительно тигля ω – в удобные для расчёта единицы измерения:

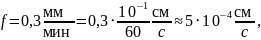
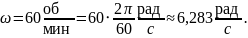
2. Рассчитаем значения площади поверхности испарения для трех значений диаметра тигля:

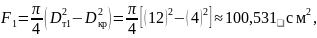
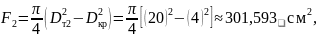
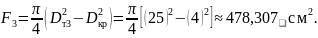
3. Проведём расчет значений толщины диффузионного слоя и эффективного коэффициента распределения.

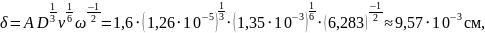
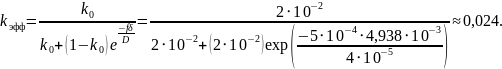
4. Рассчитаем значения приведённого коэффициента испарения для трех случаев.

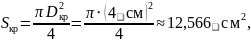
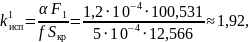
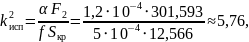
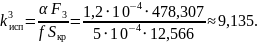
5. Рассчитаем значения обобщённого коэффициента распределения для трех случаев.

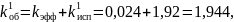
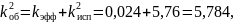
6. По известным параметрам рассчитаем начальную концентрацию и построим на рисунке 5 график зависимостей концентраций твёрдой фазы для различных значений диаметра тигля.

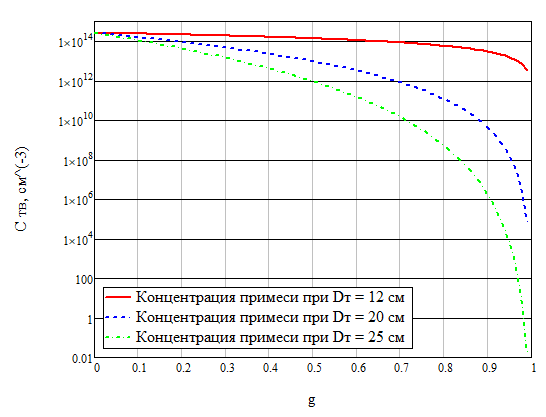
Рисунок 5 – График зависимостей концентрации твёрдой фазы от соотношения объёма твёрдой фазы и полного объёма при различных значениях диаметра тигля

6. Построить зависимости С_тв(g) для кристалла ГЭМ-7,2 при следующих параметрах технологического процесса: скорость вращения кристалла относительно тигля 60 об/мин, диаметр кристалла 4 см, диаметр тигля 25 см, скорость кристаллизации 0,3, 6, 10 мм/мин. Начальную концентрацию примеси в расплаве взять из п.4. Построить графики зависимости k_эфф и k_об от скорости кристаллизации. Для указанных параметров технологического процесса записать в таблицу значения k_эфф, k_и и k_об.

Таблица 5 – Расчётные значения k_эфф, k_исп и k_об для различных значений диаметра тигля

f, мм/мин	k	kисп	kоб
0,3	0,0242	9,135	9,159
6	0,5068	0,457	0,964
10	0,9334	0,274	1,207

1. Переведём заданные величины – скорости кристаллизации f_i и скорость вращения кристалла относительно тигля ω – в удобные для расчёта единицы измерения:

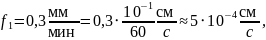
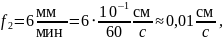
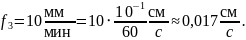
2. Рассчитаем значения площади поверхности испарения:

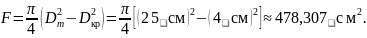
3. Проведём расчет значений толщины диффузионного слоя и эффективного коэффициента распределения для трех значений скорости кристаллизации.

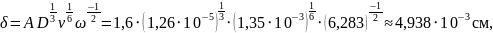
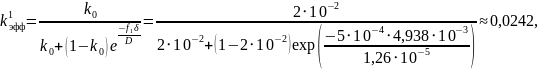
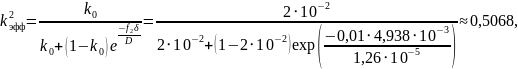
4. Рассчитаем значения приведённого коэффициента испарения для трех случаев.

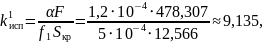
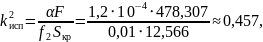
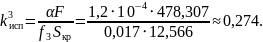
5. Рассчитаем значения обобщённого коэффициента распределения для трех случаев.

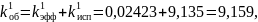
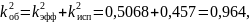
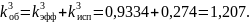
6. Построим на рисунке 6 график зависимостей концентраций твёрдой фазы для различных значений скорости кристаллизации.

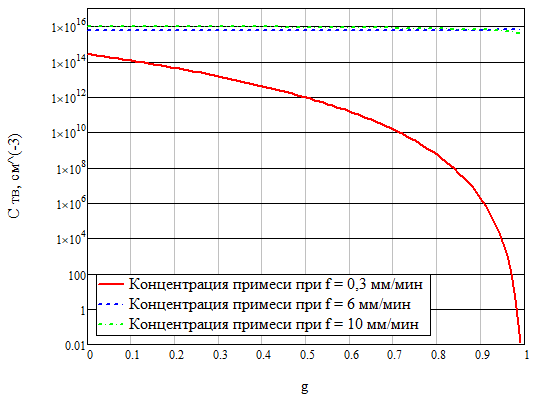
Рисунок 6 – График зависимостей концентрации твёрдой фазы от соотношения объёма твёрдой фазы и полного объёма при различных скоростях кристаллизации

7. На рисунках 7 и 8 построим графики зависимостей эффективного коэффициента распределения и обобщённого коэффициента распределения от скорости кристаллизации.

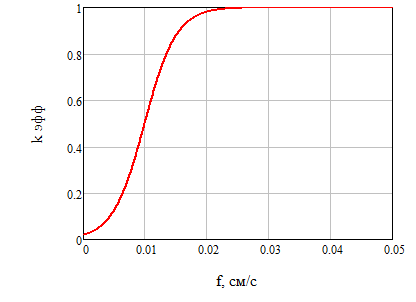
Рисунок 7 – График зависимости эффективного коэффициента распределения от скорости кристаллизации

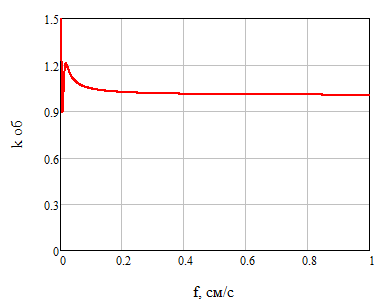
Рисунок 8 – График зависимости обобщённого коэффициента распределения от скорости кристаллизации

6. Определим технологический режим выращивания кристалла, в котором реализуется метод компенсационного испарения.

Зададим условия процесса: ω = 60 об/мин, f = 1 мм/мин, D_кр = 4 см.

Найдём диаметр тигля:

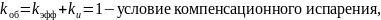
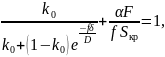
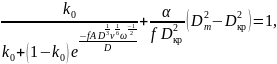
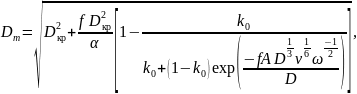
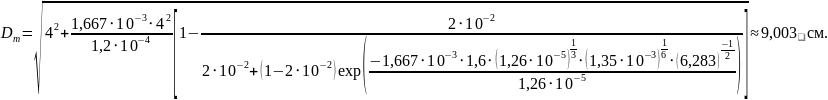
ВЫВОДЫ: в данной работе было исследовано легирование кристаллов германия галием и мышьяком при их выращивании методом Чохральского, а также то, как изменение различных параметров влияет на качество получившегося кристалла.

В пунктах 1 – 3 исследовалось легирование германия галием. При этом эффективный коэффициент распределения меньше 1, его значение увеличивается при увеличении скорости кристаллизации, так как возрастает концентрация примеси в полупроводнике. Увеличение скорости вращения кристалла относительно тигля, напротив, приводит к уменьшению эффективного коэффициента распределения примеси в материале, а также к уменьшению толщины диффузионного слоя. Значения параметров k_эфф и δ стремятся к максимальным при ω 0, а к минимальным при ω . Также в пункте 3 был проведён расчёт коэффициента эффективного распределения примеси в рамках модели регулярных растворов.

В пунктах 4 – 7 исследовалось легирование германия мышьяком, который является донорной примесью. Рассматривалось влияние выбираемых параметров процесса выращивания кристалла – скорости кристаллизации, относительной скорости вращения и диаметра кристалла на необходимое значение диаметра тигля.

В последнем пункте определён технологический режим выращивания кристаллов германия, легированного оловом, в котором реализуется метод компенсационного испарения. Концентрация примеси при этом методе остаётся постоянной. При заданных параметрах (диаметр кристалла, скорость кристаллизации, скорость вращения кристалла относительно тигля) был подобран диаметр тигля такой, что k_об ≈ 1. Полученный диаметр тигля D_т = 9,003 см превосходит диаметр кристалла – 4 см – в 2,25 раз.